并查集是一种用来管理元素分组情况的数据结构。可以高效地进行如下操作。
1.查询元素a和元素b是否属于同一组
2.合并元素a和元素b所在的组

并查集也是使用树形结构实现的。

每个元素对应一个节点,每个组对应一棵树。在并查集中,哪个节点是哪个节点的父亲以及树的形状等信息无需多加关注,整体组成一个树形结构才是重要的。
(1) 初始化
准备n个节点来表示n个元素。最开始时没有边。

(2) 合并
从一个组的根向另一个组的根连边,这样两棵树就变成了一棵树,也就把连个组合并为一个组了。

(3) 查询
为了查询两个节点是否属于同一组,我们需要沿着树向上走,来查询包含这个元素的树的根是谁。
如果两个节点走到了同一个根,那么就可以知道它们属于同一组。
在下图中,元素2和元素5都走到了元素1,因此它们属于同一组。
另一方面,由于元素7走到了元素6,因此与元素2和元素5属于不同组。

注意点
为了避免退化情况的发生,采取如下方法。
1.对于每棵树,记录这棵树的高度
2.合并时如果两棵树的rank不同,那么从rank小的向rank大的连边

此外,通过路径压缩,可以使得并查集更加高效。对于每个节点,一旦向上走到了一次根节点,就把这个点到父亲的边改为直接相连边。
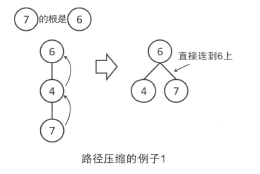
在此之上,不仅仅是所查询的节点,在查询过程中向上经过的所有的节点,都改为直接连到根上。
这样再次查询这些节点时,就可以很快知道是谁了。
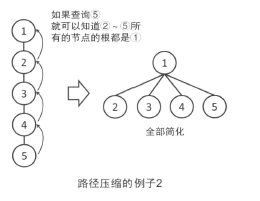
在使用这种简化的方法时,为了简单起见,即使树的高度发生变化,我们也不修改rank的值。
实现如下。par[]表示的是父亲的编号,par[x]=x时,x是所在的树的根。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int par[100]; //父亲 4 int rank[100]; //树的高度 5 6 //初始化n个元素 7 void init(int n) 8 { 9 for(int i=0; i<n; i++) 10 { 11 par[i]=i; 12 rank[i]=0; 13 } 14 } 15 //查询树的根 16 int find(int x) 17 { 18 if(par[x]==x) return x; 19 else return par[x]=find(par[x]); 20 } 21 //合并x和y所属的集合 22 void unite(int x,int y) 23 { 24 x=find(x); 25 y=find(y); 26 if(x==y) return; 27 if(rank[x]<rank[y]) 28 { 29 par[x]=y; 30 } 31 else 32 { 33 par[y]=x; 34 if(rank[x]==rank[y]) rank[x]++; 35 } 36 } 37 //判断x和y是否属于同一个集合 38 bool same(int x,int y) 39 { 40 return find(x)==find(y); 41 } 42 int main() 43 { 44 init(10); 45 unite(5,6); 46 unite(5,7); 47 cout<<same(5,8)<<endl; 48 return 0; 49 }
看个题目 食物链(POJ 1182)

分析如下 来自《挑战程序设计竞赛》


1 #include<bits/stdc++.h> 2 using namespace std; 3 int par[100]; //父亲 4 int rank[100]; //树的高度 5 6 //初始化n个元素 7 void init(int n) 8 { 9 for(int i=0; i<n; i++) 10 { 11 par[i]=i; 12 rank[i]=0; 13 } 14 } 15 //查询树的根 16 int find(int x) 17 { 18 if(par[x]==x) return x; 19 else return par[x]=find(par[x]); 20 } 21 //合并x和y所属的集合 22 void unite(int x,int y) 23 { 24 x=find(x); 25 y=find(y); 26 if(x==y) return; 27 if(rank[x]<rank[y]) 28 { 29 par[x]=y; 30 } 31 else 32 { 33 par[y]=x; 34 if(rank[x]==rank[y]) rank[x]++; 35 } 36 } 37 //判断x和y是否属于同一个集合 38 bool same(int x,int y) 39 { 40 return find(x)==find(y); 41 } 42 int T[100005],X[100005],Y[100005]; 43 int main() 44 { 45 int n,k,ans=0; 46 cin>>n>>k; 47 //初始化并查集 48 //元素x,x+n,x+2*n分别代表x-A,x_B,x-C 49 init(n*3); 50 for(int i=0;i<k;i++) 51 { 52 cin>>T[i]>>X[i]>>Y[i]; 53 54 int x=X[i]-1,y=Y[i]-1; //把输入变成0~n-1的范围 55 if(x<0||x>=n||y<0||y>=n) 56 { 57 ans++; 58 continue; 59 } 60 61 if(T[i]==1)//x和y属于同一类 的信息 62 { 63 if(same(x,y+n)||same(x,y+2*n)) 64 { 65 ans++; 66 } 67 else 68 { 69 unite(x,y); 70 unite(x+n,y+n); 71 unite(x+2*n,y+2*n); 72 } 73 } 74 else//x吃y 的信息 75 { 76 if(same(x,y)||same(x,y+2*n)) 77 { 78 ans++; 79 } 80 else 81 { 82 unite(x,y+n); 83 unite(x+n,y+2*n); 84 unite(x+2*n,y); 85 } 86 } 87 } 88 cout<<ans<<endl; 89 return 0; 90 }
