利用二分法和牛顿法开根号

一.问题描述：给定一个数，如何求它的平方根(不能使用内置函数，如sqrt()函数)。

二.题解：

　　这属于比较经典的一道题目，通常有两种方法：二分法和牛顿法，下面是详细描述。

方法1：二分法，这是比较容易想到的一种方法。通过比较中间值与最终值的大小来改变中间值，最终在满足某个精度的情况下返回这个中间值作为最终结果。代码如下：

#include<iostream>
#include<cmath>
using namespace std;
//n是大于等于1的数
double MySqrt(double n)
{
    double _max = n; //此处一定为浮点数，不要用整数
    double _min = 0.0;
    double p = 1e-5; //此处为精度，当满足该精度时，返回该近似值
    double  mid = (_max + _min) / 2.0;
    while(fabs(mid * mid - n) > p)//此处是浮点数之差的绝对值与精度进行比较
    {
        if(mid * mid < n)
            _min = mid;
        else if(mid * mid > n)
            _max = mid;
        else
            return mid;
        mid = (_max + _min) / 2.0;
    }
    return mid;
}
int main()
{
    cout<<MySqrt(80)<<endl;
}

很容易看出，该算法的时间复杂度为O(logN)，空间复杂度为O(1)。而且最终结果的精度取决于精度p的设置。

需要注意的是，对于n小于1的时候，二分法就不适用了，因为mid一定是小于1的数，而mid*mid一定会变得更小，导致区间始终向0靠近(向左靠近)，不符合二分法的特征。

注：这里面的变量类型都是浮点型！！

方法2：1.牛顿法，牛顿迭代法（Newton's method）又称为牛顿-拉夫逊方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根。另外该方法广泛用于计算机编程中。

设r是f(x) = 0的根，选取x0作为r初始近似值，过点（x0,f(x0)）做曲线y = f(x)的切线L，L的方程为y = f(x0)+f'(x0)(x-x0)，求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0)，称x1为r的一次近似值。

过点（x1,f(x1)）做曲线y = f(x)的切线，并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1)，称x2为r的二次近似值。重复以上过程，得r的近似值序列，其中x(n+1)=x(n)－f(x(n))/f'(x(n))，称为r的n+1次近似值，上式称为牛顿迭代公式。

2.而开根号的问题可以看作求解f(x) = x² - a = 0的根。

(1)在曲线f(x)=x^2-a上任取一点(x0,f(x0))，x0≠0，该点的切线方程为： 
 
(2)该切线与x轴的交点为： 
 

(3)不断用新的交点来更新原来的交点(即逼近的过程) 
根据牛顿迭代的原理，可以得到以下的迭代公式：

　　　　　　　　　　

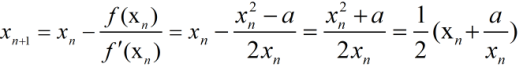
根据这个公式，可实现该算法，代码如下：

#include<iostream>
#include<cmath>
using namespace std;
double MySqrt(double n)
{
    double x = 1.0;//设置初值
    double p = 1e-5;//设置精度
    while(fabs(x*x - n) > p)
    {
        x = (x + n / x) / 2.0;
    }
    return x;
}
int main()
{
    cout<<MySqrt(82)<<endl;
}

牛顿法同二分法一样，时间复杂度为O(logN)，空间复杂度为O(1)。牛顿法每次迭代的误差都会至少小一半，所以复杂度最多是O(logN)。根据牛顿法的原理可知，迭代的次数越多，近似值越逼近真实值，当然我们会通过设置精度来限制它的迭代次数。

三.牛顿法与二分法的比较：

1.我通过测试82的平方根来比较这两种方法：

二分法：

牛顿法：

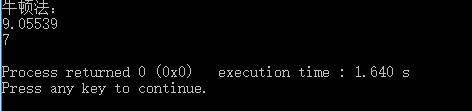
可以看出，当我设置两种算法的精度一样时，二分法迭代次数为24次，而牛顿法的迭代次数为7次;且牛顿法的准确率更高。

所以说，牛顿法与二分法相比，速度更快、准确率更高。

2.牛顿法需要设置初值(即初始的x₀)，有时问题的答案的准确率很依赖于初值的设定(可参考：https://www.zhihu.com/question/20690553)；而二分法不需要设置初值，所以稳定性较强。