一 综述
Dijkstra算法(迪杰斯特拉算法)主要是用于求解有向图中单源最短路径问题。其本质是基于贪心策略的(具体见下文)。其基本原理如下:
(1)初始化:集合vertex_set初始为{source_vertex},dist数组初始值为$dist[i] = G.arc[source\_vertex][i],i=0,1,ldots,n-1$
(2)从顶点集合V-vertex_set中选出$v_j$,满足$dist[j] = Minleft{dist[i] | v_i∈V-vertex\_set ight}$,那么$v_j$就是当前求得的一条从source_vertex出发的最短路径的终点,并令$vertex\_set = vertex\_set ∪ j$。
(3)修改从source_vertex出发到集合V-vertex_set上任一顶点$v_k$可达的最短路径长度:如果$dist[j] + arc[j][k] < dist[k]$,则令$dist[k] = dist[j] + G.arc[j][k]$。
(4)重复(2)~(3)操作共n-1次,直到所有的顶点都包含在vertex_set中。
具体代码如下:
#include<iostream>
#include<unordered_map>
#include<queue>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<sstream>
#include<set>
#include<map>
using namespace std;
#define MAX_NUM 100
#define INF 0x7fffffff
/*
dijkstra算法的实现
参数说明:
1.source_vertex:表示源点
2.G:表示图(此处以邻接矩阵为例)
3.dist数组:表示源点到其他所有顶点的最短路径的长度。例如dist[j]表示源点到顶点Vj的最短路径长度
4.vertex_set数组:表示已找到最短路径的顶点的集合,其中vertex_set[i] = true表示顶点dist[i]已经最终确定
5.pre数组:用以表示顶点的最短路径的前驱顶点。例如,pre[i] = k表示顶点vi的最短路径上的前驱顶点为vk。
*/
class Graph
{
public:
int vertexNum;//顶点个数
int arcNum;//弧的个数
int vertex[MAX_NUM];//顶点表
int arc[MAX_NUM][MAX_NUM] = {{0,INF,10,INF,30,100},
{INF,0,5,INF,INF,INF},
{INF,INF,0,50,INF,INF},
{INF,INF,INF,0,INF,10},
{INF,INF,INF,20,0,60},
{INF,INF,INF,INF,INF,0}};//弧信息表
};
void Dijkstra(Graph &G,int source_vertex,int dist[],bool vertex_set[],int pre[])
{
int _min;
int k;
int vertex_num = G.vertexNum;//顶点个数
//初始化
for(int i = 0 ; i < vertex_num; i++)
{
dist[i] = G.arc[source_vertex][i];//初始化dist数组
if(i == source_vertex)
vertex_set[i] = true;//将顶点source_vertex加入vertex_set数组
else
vertex_set[i] = false;
pre[i] = 0;//前驱顶点为v0,后面会更新
}
//遍历n-1次,每次找到一个顶点的最短路径
for(int i = 1; i < vertex_num; i++)
{
_min = INF;//初始化辅助变量
//在未获取最短路径的顶点中,找到离source_vertex最近的顶点vk。
for(int j = 0; j < vertex_num; j++)
{
if(vertex_set[j] == false && dist[j] < _min)
{
_min = dist[j];
k = j;
}
}
//此时源点到顶点vk的最短距离已经找到,即dist[k]已经确定,将k加入到vertes_set中
vertex_set[k] = true;
//对dist[j]进行检验更新
for(int j = 0; j < vertex_num; j++)
{
int tmp = (G.arc[k][j]== INF ? INF : _min + G.arc[k][j]);//防止溢出
if(vertex_set[j] == false && tmp < dist[j])
{
dist[j] = _min + G.arc[k][j];//更新满足条件的顶点的dist数组值
pre[j] = k;//更新前驱顶点
}
}
}
}
int main()
{
Graph G;
G.vertexNum = 6;
int source_vertex = 0;
int dist[6] = {0};
bool vertex_set[6];
int pre[100] = {0};
Dijkstra(G,source_vertex,dist,vertex_set,pre);
cout<<dist[0]<<endl;
}
该算法的时间的时间复杂度为O(n^3),n为图中顶点的个数。其中比较核心的部分是最里面的两个for循环,第一个for循环对应的是第二步;而第二个for循环对应的是第三步;最外层的for循环对应的是第四步。
此外,(1)由于INF表示的int能表示的最大值,它加上一个正值必然会溢出,所以应该考虑溢出的问题。(或者别把INF设成这么大,设小些)
(2)我们默认带权有向图在表示时,若果i == j,则w(i,j)=0而不是w(i,j)=∞。
二 相关理论和注意事项
1.Dijkstra算法的核心之处在于:从源点$v_0$到目标顶点$v_j$的最短路径,要么是弧$(v_0,v_j)$;要么是中间只经过vertex_set中的顶点而最后达到顶点$v_j$的路径。
证明如下:假设符合上述结论的最短路径为L1,假设从$v_0$到顶点$v_j$的最短路径上有一个顶点不在vertex_set中,则说明存在一条终点不在vertex_set中而长度比此路径更短的路径,设该路径为L2。但是,这是与事实相矛盾的。因为我们是按路径长度递增的次序来产生个最短路径的,故长度比此路径短的所有路径都已经产生,它们的终点必然在vertex_set中;即若L2 < L1,L2中的终点必然在集合vertex_set中。
2.更新集合vertex_set只在第二步,相当于每次选出最小的dist[j],实质就是一个贪心的过程;而第三部相当于更新每个满足条件的dist[j]。第二步和第三步就体现了理论中的两种情况。
3.可以根据pre数组追溯到源点到目标顶点的最短路径序列。
4.Dijkstra算法不适用于边上带有负权重的有向图,如果边上有负值的话,有可能出现当与vertex_set内某点(记为A)以负边相连的点(记为B)确定最短路径时,它的最短路径加上负边的权值结果小于A原先确定的最短路径的长度,而此时的A在dijkstra算法下是无法更新的。例如:
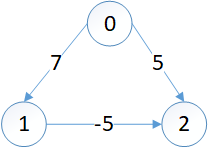
根据Dijkstra算法而言,如果求$v_0$到其他顶点的最短路径的话,首先一开始确定的是$dist[0] = 0$且$vertex\_set[0] = true$,然后由于$dist[2]$是最小的,所以$vertex\_se[2] = true$即$v_0$到$v_2$的最短路径长度为5,然而实际上$v_0$到$v_1$再到$v_2$的距离明显更小,所以实际上$v_0$到$v_2$的最短路径长度为应为7 - 5 = 2;但是$dist[2]$无法再更新了,所以此时利用Dijkstra算法求得的最短路径是错误的。