【剑指offer-21】调整数组顺序使奇数位于偶数前面，C++实现（冒泡排序）

1.题目

      输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于位于数组的后半部分。

2.思路

　　本题有两种解法，一种是不保证数组稳定性的解法，一种是保证数组稳定性的解法。数组的稳定性是指数组的奇数和奇数，偶数和偶数之间的相对位置不变。

• 不要求稳定性的解法：

      两个指针，p指向第一个元素，q指向最后一个元素。两个指针遍历数组，向后移动p使得p指向偶数，向前移动q使得q指向奇数，交换p和q的内容。指针p位于指针q后面时，结束遍历。举例：12345->15342。

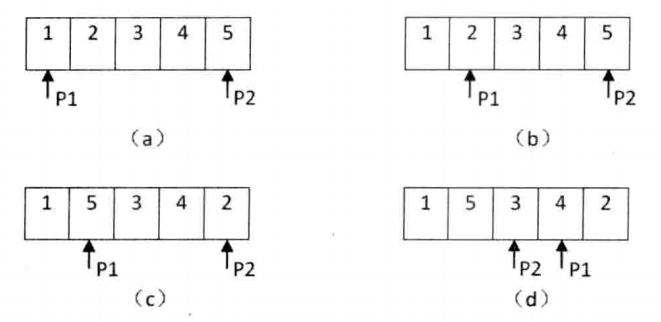
• 要求稳定性的解法：

      借鉴冒泡排序思想，每次确定一个位置。

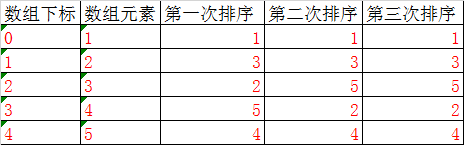
3.code

#include <iostream>
#include <vector>
using namespace std;

// 稳定的解法
class Solution_stable{
public:
    void ReArray(vector<int > &array)
    {
        // 特殊输入
        if(array.size() == 0 || array.size() == 1)
            return;

        // 冒泡排序
        for(int i = 0;i < array.size();++i)
            for(int j = array.size()-1;j>i;--j)
                if(array[j]%2 == 1 && array[j-1]%2 ==0)
                    swap(array[j],array[j-1]);
    }
};

// 不稳定的解法
class Solution_no_stable{
public:
    void ReArray(int *array2,int length)
    {
        // 特殊输入
        if(array2 == nullptr || length == 0)
            return;

        // 指针遍历数组
        int *pLeft = array2;
        int *pRight = array2 + length-1;

        while(pLeft<pRight)
        {
            // 向后移动pLeft，直到指向偶数
            while(pLeft<pRight && *pLeft %2 == 1)
                pLeft++;

            // 向前移动pRight，直到指向奇数
            while(pLeft<pRight && *pRight %2 == 0)
                pRight--;

            // 奇偶数交换
            if(pLeft < pRight)
                swap(*pLeft,*pRight);
        }
    }
};
int main()
{
    // 稳定的解法
    cout<<"稳定的解法"<<endl;
    Solution_stable solution1;
    vector<int> array = {1,2,3,4,5,6,7,8,9,10};
    solution1.ReArray(array);

    for(int i = 0;i<array.size();++i)
        cout<<array[i]<<endl;

    // 不稳定的解法
    cout<<"不稳定的解法"<<endl;
    Solution_no_stable solution2;
    int length = 10;
    int array2[10] = {1,2,3,4,5,6,7,8,9,10};
    solution2.ReArray(array2,length);

    for(int i = 0;i<length;i++)
        cout<<array2[i]<<endl;
    return 0;
} 

4.复杂度

　　时间复杂度为O(n²)

5.测试用例

• 特殊输入：空数组、含一个元素的数组
• 功能测试：奇偶交替、全部偶数在全部奇数之前、全部奇数在全部偶数之前