Vasya has the square chessboard of size n × n and m rooks. Initially the chessboard is empty. Vasya will consequently put the rooks on the board one after another.
The cell of the field is under rook's attack, if there is at least one rook located in the same row or in the same column with this cell. If there is a rook located in the cell, this cell is also under attack.
You are given the positions of the board where Vasya will put rooks. For each rook you have to determine the number of cells which are not under attack after Vasya puts it on the board.
The first line of the input contains two integers n and m (1 ≤ n ≤ 100 000, 1 ≤ m ≤ min(100 000, n2)) — the size of the board and the number of rooks.
Each of the next m lines contains integers xi and yi (1 ≤ xi, yi ≤ n) — the number of the row and the number of the column where Vasya will put the i-th rook. Vasya puts rooks on the board in the order they appear in the input. It is guaranteed that any cell will contain no more than one rook.
Print m integer, the i-th of them should be equal to the number of cells that are not under attack after first i rooks are put.
3 3
1 1
3 1
2 2
4
2
0
5 2
1 5
5 1
16
9
100000 1
300 400
9999800001
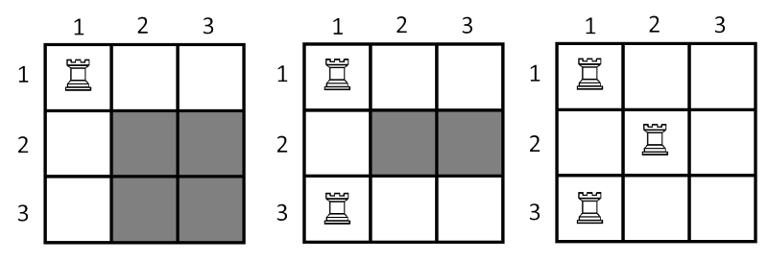
On the picture below show the state of the board after put each of the three rooks. The cells which painted with grey color is not under the attack.
#include<bits/stdc++.h> typedef long long LL; using namespace std; LL n,m,x,y; set<LL>a,b; int main() { cin>>n>>m; for(int i=1;i<=m;i++) { cin>>x>>y; a.insert(x); b.insert(y); cout<<(n-a.size())*(n-b.size())<<endl; } }