拉格朗日乘子法是解决极值问题的方法。
本方法是计算多元函数在约束条件下的极值问题的方法。
1、多元函数与约束问题
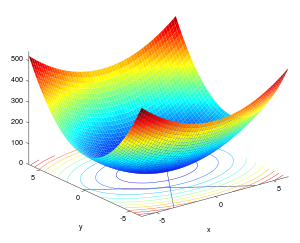
如下图所示,f(x,y)为多元函数,g(x,y)=c为约束条件。目的是计算在约束条件下多元函数的极值。
虚线为f(x,y)=d d取不同的值时,将原始图像投影到xy平面时的等高线,在等高线上的f函数值相等;
淡蓝色实线为g(x,y)为xy平面的曲线,对应于不同的(x,y)。比如g(x,y)=x+y=1,即x+y=1为约束条件。
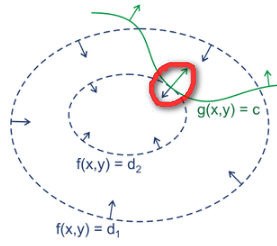
那么怎样去寻找极值点?
思路:沿着g(x,y)曲线不断前进,找到与g(x,y)与等高线的交点,所有的交点中的极值,即为需要求得的极值。如上图红色圈所示。
此时极值点满足的条件:g(x,y)与极值点所在的等高线是相切的。所以满足

根据以上原理,构建拉格朗日函数:(此时用g(x,y)代替[g(x,y)-c])
![]()
L对x,y,λ分别求偏导,并且偏导其偏导满足:
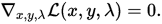
偏导分别满足:
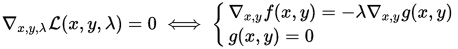
根据得到的偏导等式,求得x,y的值,即可得到f(x,y)的极值。
同样当g(x,y)<0时,等高线与约束函数的图像变成了等高线与某一块区域的集合。此时求极值时,直接求f(x,y)对x,y的偏导数,得到极值。
等价于将λ置为0时,求L对x,y求偏导。上述是拉格朗日乘子法的来源。
2、约束条件的扩展
第一部分讲解了一个约束条件,而实际中通常会用到多个约束条件。当引入下列约束条件时:
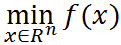
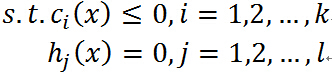
即要求f0(x)的极值,其约束条件为fi(x) hi(x).此时的拉格朗日函数为:
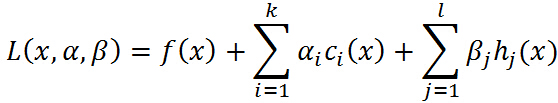
![]()
其中ª ß为拉格朗日乘子。并且ª>0,满足第一部分所阐述的λ的条件。
上述条件表述为KKT条件:
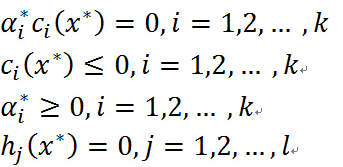
固定变量x,求L关于ª ß的最大值:
![]()
并且有:
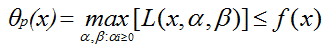
对θp求极小值可得:
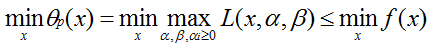
此时,求θp极小值与原始问题即求f(x)的极小值等价。
定义原始问题的最优:
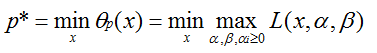
引入对偶问题:
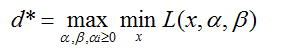
可以证明:
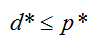
对偶问题证明:
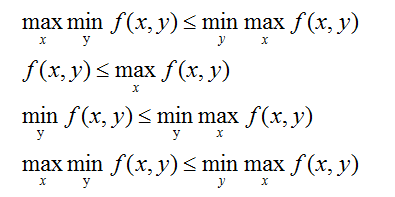
使用上述条件:
1、对L取关于变量x的偏导
2、通过偏导式子求出x关于ª ß的表达式
3、将ª ß的表达式代入L
4、得到max(L)关于ª ß的表达式
5、通过其他约束条件求出最终的极值点
举例:
SVM
对偶问题满足等号的条件:
KKT条件中的约束不等式为凸函数,等式为仿射函数,且可行域存在严格满足约束条件的点。