转载请注明出处:http://www.cnblogs.com/wangyingli/p/5928308.html
在上一篇博客《数据结构与算法(二),线性表》中介绍了线性表的创建、插入、删除等基本操作,这一篇将总结一下链表中最常考的面试题。
目录:
- 1、从尾到头打印单链表
- 2、在O(1)时间删除链表结点
- 3、链表中倒数第k个结点
- 4、反转链表
- 5、合并两个有序链表
- 6、复杂链表的复制
- 6、两个链表的第一个公共结点
- 7、判断链表是否有环
- 8、求链表环的长度
- 9、链表中环的入口结点
- 10、删除链表中重复的的结点
说明:为了测试方便,这里结点中存放数据的类型定义为int型。无特殊说明时,其结点结构为:
public class Node {
int element;
Node next;
Node(int element) {
this.element = element;
}
}
另外在这篇文章中方法的输入参数,head表示的是首元结点,不是头结点。如,reversePrint(Node head)表示传入的参数为首元结点。
1、从尾到头打印单链表
题目:输入一个链表的「头结点」,从尾到头反过来打印出每个结点的值。(剑指offer,第5题)
方法1:这里的头结点,其实指的是首元结点,和链表创建时的头结点不同,这点需要注意。从尾到头打印单链表,也就是第一个结点最后一个打印,最后一个结点第一个打印,这是典型的「后进先出」。首先想到的是使用一个辅助栈,先将所有结点依次放入栈中,然后遍历栈实现反转打印。代码如下:
//栈实现
public void reversePrint(Node head) {
if(head == null)
return;
Stack<Node> stack = new Stack<Node>();
Node current = head;
while(current != null) {
stack.push(current);
current = current.next;
}
while(!stack.isEmpty()) {
System.out.print(stack.pop().element + " ");
}
}
方法2:由于递归的本质就是一个栈结构,因此我们也可以使用递归来实现反转打印。每次访问一个结点时,先递归输出它后面的结点,在输出结点自身。代码如下:
//递归实现
public void reversePrint(Node head) {
if(head == null)
return;
Node current = head;
reversePrint(current.next);
System.out.print(current.element + " ");
}
注意:
- 虽然递归实现代码比较简洁,但当链表非常长时,会导致调用栈溢出。而显示使用栈来实现反转打印不会出现这种问题,其鲁棒性更好。
- reversePrint方法的输入参数为首元结点,不是头结点,调用这个方法时需注意。
2、在O(1)时间删除链表结点
题目:给定单向链表的头指针和一个结点指针,定义一个函数在 O(1)时间删除该结点。(剑指offer,第13题)
这是一道经典的google面试题,一般来说要想删除单向链表中的一个结点(current),必须要知道该结点前面一个结点(prior),然后使用prior.next = prior.next.next 方法来删除该结点。但是单向链表中不能反向获取前一个结点,只能通过顺序遍历链表来获取,这时时间复杂度为 O(n),明显不符合要求。
其实换个思路,一个结点删除自身很麻烦,删除它的下一个结点(next)却很简单,只需要 O(1)的时间。我们只需将结点next的值覆赋给current(此时current原来的值被覆盖),然后再删除next即可。另外若current是尾结点则必须遍历以获取前一个结点。
public void deleteCurrent(Node head, Node current) {
if(head == null || current == null)
return;
if(current.next != null) { //current不是尾结点
current.element = current.next.element;
current.next = current.next.next;
}else if(head == current) { //只有一个结点,必须在current.next != null之后
head = null;
current = null;
} else { //是尾节点
Node node = head;
while(node.next != current) {
node = node.next;
}
node.next = null;
}
}
时间复杂度分析:
对于前 n-1 个结点其时间复杂度为 O(1),尾结点其时间复杂度度为 O(n),因此其平均时间复杂度为
另外需要注意,上述代码基于一个假设:要删除的结点在链表中。判断一个结点是否在链表中需要 O(n) 的时间。受 O(1)的时间限制,我们把确保结点在链表中的责任推给了调用者。
3、链表中倒数第k个结点
题目:输入一个链表,输出该链表中倒数第 k 个结点。如:一个链表为 1 -> 2 ->3 -> 4 -> 5 -> 6,其倒数第3个结点为 4。(剑指offer,第15题)
若整个链表有n个结点,那么倒数第k个结点就是从头结点开始的第n-k+1个结点,只需遍历一次链表找到这个结点即可。幸运的是在上一篇《数据结构与算法(二),线性表》中创建的链表能够通过size( )方法在 O(1)时间获取链表的长度。但有时链表是以首元结点的形式给出的,这时我们就需要首先遍历一次链表以获取其长度,然后才能运用上面的方法。也就是说需要遍历两次链表,第一次统计结点个数,第二次查找第n-k+1个结点。
一种改进方法是定义两个指针,从链表首元结点开始第一个指针先向前走 k-1 步,然后两个指针一起向前遍历,直到第一个指针到达链表的尾结点,此时第二个指针所指的结点即为所求。这里注意以下情况需要进行特殊处理:
- 链表结点总数小于k
- k为0
- 链表为null
代码如下:
public Node findKthToTail(Node head, int k) {
if(head == null || k == 0)
return null;
Node aNode = head;
for (int i=0; i<k-1 ; i++ ) {
if(aNode.next == null) {
return null;
}
aNode = aNode.next;
}
Node bNode = head;
while(aNode.next != null) { //尾结点不为空
aNode = aNode.next;
bNode = bNode.next;
}
return bNode;
}
4、反转链表
题目:定义一个函数,输入一个链表的头结点,反转该链表并输出反转后链表的头结点。如:一个链表为 1 -> 2 ->3 -> 4 -> 5 -> 6,其反转链表为 6 -> 5 -> 4 -> 3 -> 2 -> 1。(剑指offer,第16题)
方法1:借助于栈的先进后出的特点反转链表,具体做法是先将链表的结点按顺序依次入栈,然后再依次出栈并链接在一起,最后返回首元结点的引用
// 链表反转,借助于栈实现
public Node reverseList(Node head) {
if(head == null || head.next == null) //链表为空或只有一个元素,无需反转
return head;
Stack<Node> stack = new Stack<Node>();
Node current = head;
while(current != null) {
stack.push(current);
current = current.next;
}
Node reverse = stack.pop();
current = reverse;
while(!stack.isEmpty()) {
current.next = stack.pop();
current = current.next;
}
current.next = null; //【防止形成循环链表】
return reverse;
}
方法2:递归实现,我们假设链表最后N-1个结点已经完成反转,则此时链表的状态如下图,现在只需将current插入到结果链表的末端。 注意:最后一定要加上current.next = null否则将出现环。
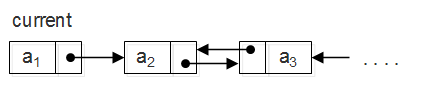
代码实现:
//链表反转,递归实现(注意递归的地方)
public Node reverseList(Node head) {
if(head == null || head.next == null)
return head;
Node current = head;
Node reverse = reverseList(current.next);
current.next.next = current;
current.next = null; // 防止出现环
return reverse;
}
方法3:迭代实现(最优)。需要三个引用,如下图所示,aNode指向反转后链表的首结点,bNode指向原链表中剩余结点的首结点,cNode指向原链表中剩余结点的第二个结点。在每轮迭代中,将bNode插入到逆链表的开头。
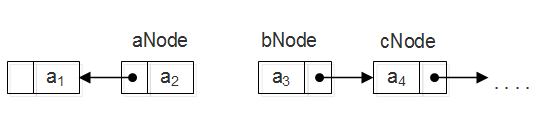
代码如下:
//链表反转,迭代实现
public Node reverseList(Node head) {
Node aNode = null;
Node bNode = head;
Node cNode = null;
while(bNode != null) {
cNode = bNode.next;
bNode.next = aNode;
aNode = bNode;
bNode = cNode;
}
return aNode;
}
5、合并两个有序链表
题目:输入两个递增排序的链表,合并这两个链表并使新链表中的结点仍按递增排序。(剑指offer,第17题)。如:
链表a: 1 -> 3 -> 5 ->7
链表b: 2 -> 4 -> 6 ->8
合并后: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8
方法1:递归实现,两个链表的初始状态如下图,首先比较两个链表的首结点,将较小的首结点链接到「已经合并的链表」之后,此时两个链表剩下的部分依然有序,可以递归调用函数合并链表。注意:两个链表为空的情况。
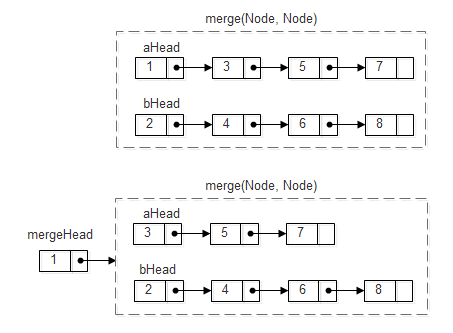
代码如下:
public Node merge(Node aHead, Node bHead) {
if(aHead == null)
return bHead;
if(bHead == null)
return aHead;
Node mergeHead = null;
if(aHead.element > bHead.element) {
mergeHead = bHead;
mergeHead.next = merge(aHead, bHead.next);
}else {
mergeHead = aHead;
mergeHead.next = merge(aHead.next, bHead);
}
return mergeHead;
}
方法2:递归的方法可能比较难理解,这里给出一种直接的解法。首先比较两个链表的首结点,获取合并后链表的首结点,然后依次比较剩下部分的首结点,直到一个链表为空,最后将不为空的链表链接到「已经合并的链表」之后。
public Node merge(Node aHead, Node bHead) {
if(aHead == null)
return bHead;
if(bHead == null)
return aHead;
//求合并后链表的首结点
Node mergeHead = null;
Node current = null;
if(aHead.element > bHead.element) {
mergeHead = bHead;
bHead = bHead.next;
}else {
mergeHead = aHead;
aHead = aHead.next;
}
current = mergeHead;
while(aHead != null && bHead != null) {
if(aHead.element > bHead.element) {
current.next = bHead;
bHead = bHead.next;
}else {
current.next = aHead;
aHead = aHead.next;
}
current = current.next;
}
//合并剩余部分
if(aHead == null) { //a链表为空,
current.next = bHead;
}else { //b为空
current.next = aHead;
}
return mergeHead;
}
6、复杂链表的复制
题目:复制一个复杂链表,在复杂链表中,每个结点除了有一个指针指向下一个结点外,还有一个指针指向链表中的任意结点或NULL。(剑指offer,第26题)
复杂链表中的结点结构:
public class ComplexNode() {
int element;
ComplexNode next;
ComplexNode random;
}
方法1:直接复制,首先复制原始链表中每个结点,并使用next指针链接起来;然后再遍历原始链表,设置每个结点的random指针。若当前结点C的random域指向结点S,由于S可能位于C的前面也可能位于C的后面,所以为了确定S的在链表中的位置,每次都需从头开始遍历链表。
public ComplexNode cloneComplexList(ComplexNode pHead){
//链表为空或只有一个元素
if(pHead == null)
return pHead;
if(pHead.next == null)
return new ComplexNode(pHead.element);
//复制原始链表
ComplexNode cloneHead = new ComplexNode(pHead.element);
ComplexNode cloneCurrent = cloneHead;
ComplexNode pCurrent = pHead;
while(pCurrent.next != null) {
cloneCurrent.next = new ComplexNode(pCurrent.next.element);
cloneCurrent = cloneCurrent.next;
pCurrent = pCurrent.next;
}
//复制random域
pCurrent = pHead;
cloneCurrent = cloneHead;
while(pCurrent != null) {
if(pCurrent.random != null) {
//定位random指向的位置
int index = 0;
ComplexNode temp = pHead;
while(temp != pCurrent.random) {
index++;
temp = temp.next;
}
temp = cloneHead;
while(index != 0) {
index--;
temp = temp.next;
}
cloneCurrent.random = temp;
}
pCurrent = pCurrent.next;
cloneCurrent = cloneCurrent.next;
}
return cloneHead;
}
由于定位每个结点的random都需从头开始遍历链表,因此此方法的时间复杂度为 O(n^2^)。
方法2:利用哈希表,由于方法1的主要时间花费在了定位结点的random上,我们可以利用哈希表建立原链表结点与复制后链表结点的对应关系,这样就可以在O(1)的时间找到random。
public ComplexNode cloneComplexList(ComplexNode pHead){
//链表为空或只有一个元素
if(pHead == null)
return pHead;
if(pHead.next == null)
return new ComplexNode(pHead.element);
//复制原始链表
Map<ComplexNode, ComplexNode> map = new HashMap<>();
ComplexNode cloneHead = new ComplexNode(pHead.element);
ComplexNode cloneCurrent = cloneHead;
ComplexNode pCurrent = pHead;
map.put(pCurrent, cloneCurrent);
while(pCurrent.next != null) {
cloneCurrent.next = new ComplexNode(pCurrent.next.element);
cloneCurrent = cloneCurrent.next;
pCurrent = pCurrent.next;
map.put(pCurrent, cloneCurrent);
}
//复制random域
pCurrent = pHead;
cloneCurrent = cloneHead;
while(pCurrent != null) {
if(pCurrent.random != null) {
cloneCurrent.random = map.get(pCurrent.random); // O(1)
}
pCurrent = pCurrent.next;
cloneCurrent = cloneCurrent.next;
}
return cloneHead;
}
此方法相当于用空间换时间,使用大小为O(n)的哈希表,将时间复杂度由O(n^2^)降为 O(n)。
方法3:不用辅助空间
- 第一步,复制原链表中的每个结点,若N的复制结点为N',并将N'插入到N的后面组成一个长链表;
- 第二步,若原链表中结点N的random指向结点S,则复制结点N'指向结点S'(S的复制结点),设置复制结点的random域;
- 第三步,将长链表拆分为两个链表,奇数位置的结点链接为原链表,偶数位置的结点链接为复制的链表。
其复制过程如下:
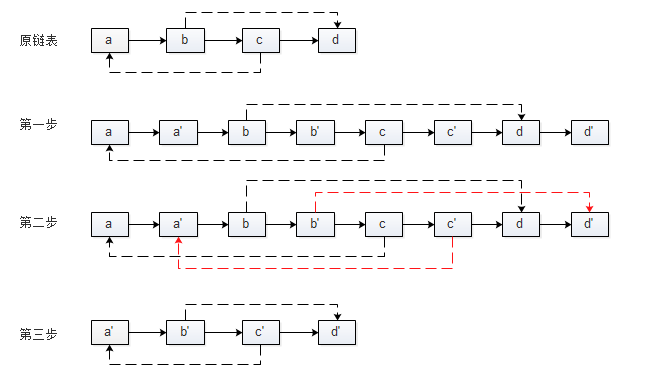
代码如下:
public ComplexNode cloneComplexList(ComplexNode pHead){
if(pHead == null)
return pHead;
if(pHead.next == null)
return new ComplexNode(pHead.element);
//第一步
ComplexNode pCurrent = pHead;
ComplexNode temp;
while(pCurrent != null) {
temp = new ComplexNode(pCurrent.element);
temp.next = pCurrent.next;
pCurrent.next = temp;
pCurrent = pCurrent.next.next;
}
//第二步,复制random域
pCurrent = pHead;
while(pCurrent != null) {
if(pCurrent.random != null) {
pCurrent.next.random = pCurrent.random.next;
}
pCurrent = pCurrent.next.next;
}
//第三步,拆分长链表
ComplexNode cloneHead = pHead.next;
ComplexNode cloneCurrent = cloneHead;
pCurrent = pHead;
pCurrent.next = cloneCurrent.next; //从长链表中删除复制的结点,
pCurrent = pCurrent.next;
while(pCurrent != null) {
cloneCurrent.next = pCurrent.next;
cloneCurrent = cloneCurrent.next;
pCurrent.next = cloneCurrent.next; //从长链表中删除复制的结点,【关键】
pCurrent = pCurrent.next;
}
return cloneHead;
}
注意:拆分链表时,不但要拆分出复制后的链表,还要将原链表还原。方法3是通过将长链表中的复制结点删除的方法来还原原链表的。
6、两个链表的第一个公共结点
题目:输入两个链表,找到它们的第一个公共结点。其可能的结构有:
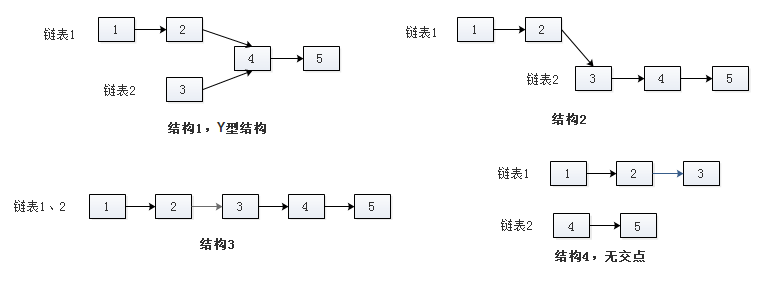
方法1:暴力方法,在第一条链表上顺序遍历每个结点,每遍历到一个结点就遍历第二条链表,看在第二条链表上是否有结点与其相同。
public Node findFirstCommonNode(Node head1, Node head2) {
Node current1 = head1;
while(current1 != null) {
Node current2 = head2;
while(current2 != null) {
if(current1 == current2)
return current1;
current2 = current2.next;
}
current1 = current1.next;
}
return null;
}
显然,若两链表长度分别为m、n,则此算法的时间复杂度为 O(m*n)。
方法2:利用栈,从前面的图可以看出,若两链表有公共结点,则从第一个公共结点开始,之后它们的所有结点都重合,。若从链表的尾部开始向前比较,则最后一个相同的结点即为第一个公共结点。「后进先出」
代码如下:
public Node findFirstCommonNode(Node head1, Node head2) {
Stack<Node> stack1 = addToStack(head1);
Stack<Node> stack2 = addToStack(head2);
Node lastNode = null;
while(!stack1.isEmpty() && !stack2.isEmpty()) {
lastNode = stack1.pop();
if(lastNode != stack2.pop()) {
return lastNode.next; //Y型结构,结构1,结构4
}
}
//结构2,3
if(stack1.isEmpty())
return head1;
if(stack2.isEmpty())
return head2;
//好像不会执行到?
return null;
}
private Stack<Node> addToStack(Node head) {
Node current = head;
Stack<Node> stack = new Stack<>();
while(current != null) {
stack.push(current);
current = current.next;
}
return stack;
}
此算法的时间复杂度与空间复杂度都为 O(m + n)。「用空间换时间」。
方法3:最常用的方法,首先遍历两个链表得到它们的长度L1、L2(不妨设L1 > L2),然后较长的链表先走(L1 - L2)步,接着再同时遍历两链表,找到的第一个相同的结点即为所求。
public Node findFirstCommonNode(Node head1, Node head2) {
int len1 = getLength(head1);
int len2 = getLength(head2);
Node current1 = head1;
Node current2 = head2;
if(len1 >= len2) {
for(int i=0; i<len1-len2; i++) {
current1 = current1.next;
}
}else {
for(int i=0; i<len2-len1; i++) {
current2 = current2.next;
}
}
while(current1 != null) {
if(current1 == current2)
return current1;
current1 = current1.next;
current2 = current2.next;
}
return null;
}
private int getLength(Node head) {
Node current = head;
int i = 0;
while(current != null) {
i++;
current = current.next;
}
return i;
}
此方法时间复杂度为O(m + n),并且不再需要辅助栈,因此提高了空间效率。
方法4:最简洁,也最难理解的方法。。废话不多说,先上代码。
public Node findFirstCommonNode(Node head1, Node head2) {
Node p1 = head1;
Node p2 = head2;
while(p1 != p2) {
p1 = (p1 == null ? head2 : p1.next);
p2 = (p2 == null ? head1 : p2.next);
}
return p1;
}
两个指针p1、p2每次走一步,若两链表长度相同,
- 若有公共结点,遍历到公共结点时p1 = p2返回;
- 若无公共结点,遍历到尾部NULL时p1 = p2,返回NULL
若两链表长度不同,指向短链表指针先走完,然后指向长链表,指向长链表指针后走完,然后指向短链表。此时等效为长度相同,如下图
- 过程同上面「两链表长度相同时」
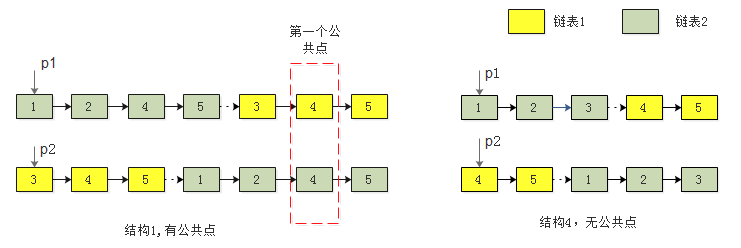
此算法的时间复杂度同样为 O(m + n)
7、判断链表是否有环
题目:一个链表,判断其是否又环。
如果一个链表有环,那么用一个指针遍历将永远也走不到尽头。使用两个指针遍历:first每次走一步,second每次走两步。若链表有环则它们一定会相遇。
代码如下:
//判断链表是否有环
public boolean hasLoop(Node head) {
Node first = head;
Node second = head;
//【判断条件second在前,second.next在后,否则可能会报空指针异常】
while(second != null && second.next != null ) {
first = first.next;
second = second.next.next;
if(first == second)
return true;
}
return false;
}
8、求链表环的长度
题目:一个链表,求其环的长度。
若链表无环,则其长度为0;若链表有环,则second和first指针相遇时,相遇点一定在环中。记录下相遇点,first再次走到该点时走到长度即为所求。
//得到相遇点
private Node getMeetNode(Node head) {
Node first = head;
Node second = head;
//【判断条件second在前,second.next在后,否则可能会报空指针异常】
while(second != null && second.next != null ) {
first = first.next;
second = second.next.next;
if(first == second)
return first;
}
return null;
}
public int getLoopLength(Node head) {
Node meetNode = getMeetNode(head);
if(meetNode == null) //无环
return 0;
Node first = meetNode.next;
int result = 1;
while(first != meetNode) {
result++;
first = first.next;
}
return result;
}
9、链表中环的入口结点
题目:一个链表中包含环,请找出该链表的环的入口结点。(剑指offer,第56题)
方法1:若知道环的长度 len (第8题已求),定义两个指针first、second,让first先走 len 步,然后first和second一起向前走,两者必然会相遇,相遇点即为环的入口结点。
//getLoopLength方法见第8题
public Node entryNodeOfLoop(Node head){
Node first = head;
Node second = head;
int len = getLoopLength(head);
if(len == 0)
return null;
for(int i=0; i<len; i++) {
first = first.next;
}
while(first != null) {
if(first == second) {
return first;
}
first = first.next;
second = second.next;
}
return null;
}
方法2:借助于HashMap或HashSet,遍历链表,遇到第一个已遍历过的结点即为环的入口结点。
//借助于set
public Node entryNodeOfLoop(Node head) {
Set<Node> set = new HashSet<>();
Node current = head;
while(current != null) {
if(!set.add(current)) {
return current;
}
current = current.next;
}
return null;
}
//或者借助于map
public Node entryNodeOfLoop(Node head){
Map<Node, Boolean> map = new HashMap<>();
Node current = head;
while(current != null) {
if(map.containsKey(current)) {
return current;
}
map.put(current, true);
current = current.next;
}
return null;
}
10、删除链表中重复的的结点
题目:在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。 例如,链表1->2->3->3->4->4->5 处理后为 1->2->5 。(剑指offer,第57题)
请注意,这里链表是排好序的。
代码如下:
public Node deleteDuplication(Node head){
if(head==null || head.next==null)
return head;
Node current = head;
if(current.val!=current.next.val){
current.next = deleteDuplication(current.next);
return current;
}else {
int val = current.val;
while(current.val==val){
current = current.next;
if(current==null)
return null;
}
return deleteDuplication(current);
}
}
好了,就先总结到这里吧。将来找工作刷题时,再来补充。