今天是2020年3月5日星期四。预计开学时间不会早于四月初,真是好消息,可以有大把的时间整理知识点(实际上发文章的时间都6月6号了,希望9月份能开学啊,不耽误找工作~)。每次导师找,整个人会变的特别烦躁,烦躁加不安,其它事情一点都做不下去,焦虑。改小论文这几天耽误了一些时间,查了些EM算法的例子,怎样理解这个算法呢?通过这周的学习,觉得数学公式有点唬人,但却是理解该算法最好的形式。
刚开始对这个算法一无所知,通过知乎、CSDN看资料,看白板视频,看讲解例子。越看例子越觉得负担重,因为要先把例子理解了,再去理解这个知识点。例子不能彻底理解,知识点也走不下去,倒不如一遍一遍的看数学公式。看完了公式,再去看例子,朦朦胧胧的就懂了。之后再去看白板视频,绝对是不一样的体验。
先看别人的视频,然后自己去推导公式,你会觉得困难摸不到头脑;先自己去推导公式,再去看别人视频,你会觉得心旷神怡一目了然。第一种做法,往往看视频的时候就是懵懵哒,抓不住别人讲述的重点;第二种做法,类似于先学会了九阳神功,再去和别人切磋武艺。初心是将《统计学习方法》这本书做详细的心得笔记,现在有点松动,希望能坚持下去。
GitHub:https://github.com/wangzycloud/statistical-learning-method
EM算法
引入
EM算法应该作为一种通用的求解方法,用于含有隐变量的概率模型参数的极大似然估计。拆开来看,这句话是应用在概率模型上的;用来估计概率模型的参数;类似于极大似然估计;求解的是含有隐变量的概率模型。那么问题来了,什么是该有隐变量的概率模型?概率模型是什么样子?极大似然估计?该方法是怎么进行计算的呢?
通常来讲,EM算法是一种迭代算法,每次迭代由两步组成:E步,求期望;M步:求极大,所以该算法被称为期望极大算法。说该算法可以作为一种通用的求解方法,原因在于:该算法不是NBM、LR、SVM这类解决相应场景的模型,而是可以用于求解含有隐变量概率模型的参数估计。
提到模型,脑子里第一印象有判别模型、生成模型。这里的概率模型自然和判别模型、生成模型不在同一个层次。在我的理解里,概率模型是类似于朴素贝叶斯算法这种,用概率来表示最后的分类标准;而不是感知机、SVM这种利用确信度来表达分类结果的模型。再考虑一下朴素贝叶斯算法,特征向量里的随机变量X,以及表示类别的随机变量Y,都是可以被观测到变量。在所有随机变量都可以观测到的情况下,我们可以利用极大似然估计来求解模型的参数。对于含有隐变量的概率模型,要如何求解呢?含有隐变量意味着不能观测到数据的全部状况,也就没有办法直接利用极大似然估计来求解。
现在看到的EM算法,就是一种求解含有隐变量的概率模型参数的极大似然估计方法。
EM算法
书本上三硬币模型,挺好的~代码已整理到github中,实际上就是把书本公式用代码实现出来...难度不大。


文中提到,该问题没有解析解,只有通过迭代的方法进行求解。仔细观察一下公式(9.4),log(x)作用在公式(9.3)上,很明显log连乘可以变成连加,但连加式子中的每个项仍然是连加式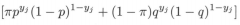 。好像是因为这个原因,就无法得到解析解了。个人对数学不感冒,只能硬性的记住“不容易求解析解”这点,至于原因,实在是搞不懂啊。虽然无法得到解析解,但我们可以通过EM算法求解,大致步骤如下:
。好像是因为这个原因,就无法得到解析解了。个人对数学不感冒,只能硬性的记住“不容易求解析解”这点,至于原因,实在是搞不懂啊。虽然无法得到解析解,但我们可以通过EM算法求解,大致步骤如下:



一般的,用Y表示观测随机变量的数据,Z表示隐随机变量的数据,Y和Z连在一起称为完全数据,观测数据Y又称为不完全数据。假设给定观测数据Y,其概率分布是P(Y|θ),其中θ是需要估计的模型参数,那么不完全数据Y的似然函数是P(Y|θ),对数似然函数L(θ)=logP(Y|θ),假设Y和Z的联合概率分布是P(Y,Z|θ),那么完全数据的对数似然函数是logP(Y,Z|θ)。
EM算法通过迭代求解L(θ)=logP(Y|θ)的极大似然估计,每次迭代由两个步骤:E步,M步组成。

文中对Q函数做了具体解释:

关于EM算法的几点说明,应该挺好理解的吧。步骤(1),迭代求解的方式需要一步步接近极值,是在某个解的基础上,进一步求解。在最开始的时候,初值是任意选择的,并且正是因为初值任意选择,容易陷入局部极值,也就是对初值的选择非常敏感(对比一下梯度下降的过程)。步骤(2),我们要清楚,求解的对象是变元参数θ。步骤(3),极大化的过程,详见下图~(θ,L(θ))图像。步骤(4),迭代停止条件。
EM算法的导出、收敛性,以及推广详见下图吧~搞了四五天,弄了个流程...

GMM高斯混合模型
书中公式一大堆,不太友好,手写代码的过程,就是把书本公式复现了一遍。难度不大,我认为需要先了解GMM模型是啥,再通过例子,熟悉一下计算过程,就可以掌握了。
还是从生成数据的角度看,由GMM模型生成一个数据,是要根据一个普通的多项式分布αk,来选择第k个高斯分布,分两步生成数据。但是,这里获得的数据,并不知道来自第几个αk,这就是隐变量了。

对于高斯混合模型的参数估计,可以通过EM算法求解。
1.明确隐变量,写出完全数据的对数似然函数。
2.EM算法的E步:确定Q函数。
3.确定EM算法的M步。
具体公式(9.26)-公式(9.32)就不一一摘录了,github已复现。算法描述如下:


本节整理的内容有些水...
代码效果