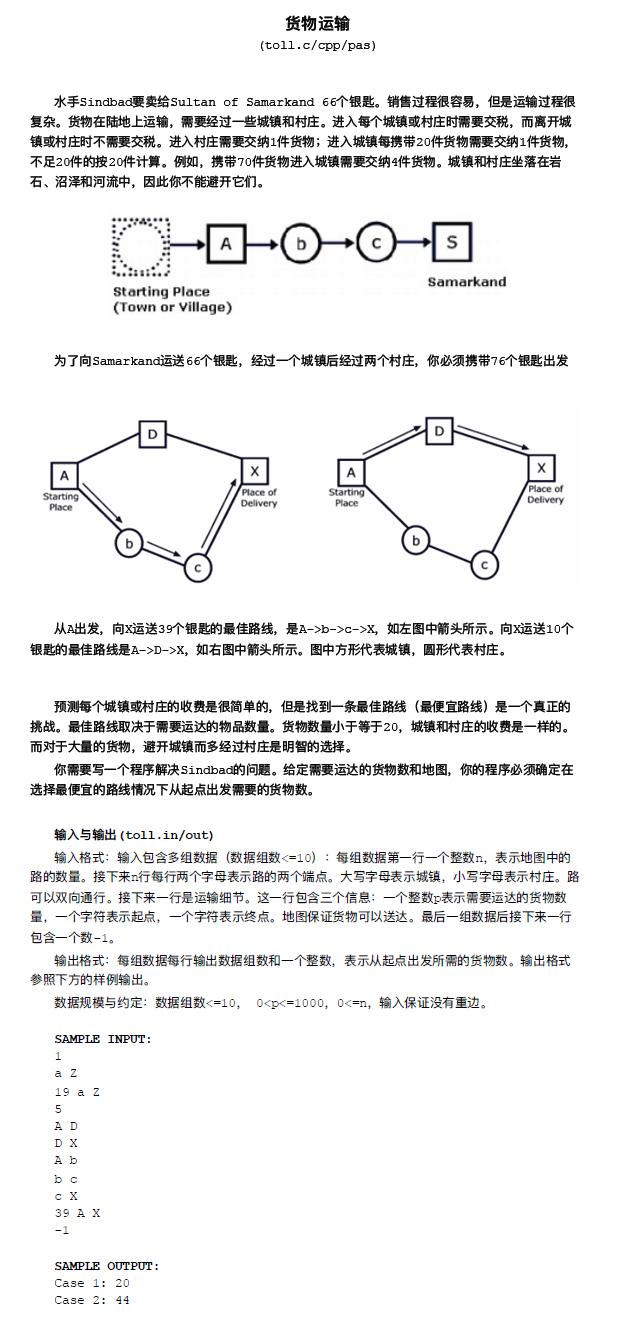
刘汝佳蓝书上的题,标程做法是从终点倒着$spfa$,我是二分答案正着$spfa$判断可不可行。效果是一样的。
【注意】多组数据建边一定要清零啊QAQ!!!
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; int S, T, p; struct Node { int v, nex; Node ( int v = 0, int nex = 0 ) : v ( v ), nex ( nex ) { } } Edge[20005]; int h[10005], stot; void add ( int u, int v ) { Edge[++stot] = Node ( v, h[u] ); h[u] = stot; } int vis[10005], dis[10005]; queue < int > q; bool Spfa ( int mid ) { memset ( vis, 0, sizeof ( vis ) ); memset ( dis, -0x3f3f3f3f, sizeof ( dis ) ); q.push ( S ); vis[S] = 1; dis[S] = mid; while ( !q.empty ( ) ) { int u = q.front ( ); q.pop ( ); vis[u] = 0; for ( int i = h[u]; i; i = Edge[i].nex ) { int v = Edge[i].v; if ( v > 25 && dis[v] < dis[u] - 1 ) { dis[v] = dis[u] - 1; if ( !vis[v] ) { vis[v] = 1; q.push ( v ); } } else if ( v <= 25 && ( dis[v] < dis[u] - ( dis[u] + 19 ) / 20 ) ) { dis[v] = dis[u] - ( dis[u] + 19 ) / 20; if ( !vis[v] ) { vis[v] = 1; q.push ( v ); } } } } return dis[T] >= p; } bool Check ( int mid ) { return Spfa ( mid ); } int erfen ( ) { int l = p, r = 10000000, ans; while ( l <= r ) { int mid = ( l + r ) >> 1; if ( Check ( mid ) ) r = mid - 1, ans = mid; else l = mid + 1; } return ans; } int main ( ) { freopen ( "toll.in", "r", stdin ); freopen ( "toll.out", "w", stdout ); int ti = 0, n; while ( scanf ( "%d", &n ) == 1 ) { if ( n == -1 ) break; memset ( h, 0, sizeof ( h ) ); for ( int i = 1; i <= n; i ++ ) { char u, v; scanf ( " %c %c", &u, &v ); add ( u - 'A', v - 'A' ); add ( v - 'A', u - 'A' ); } char s, t; scanf ( "%d %c %c", &p, &s, &t ); S = s - 'A'; T = t - 'A'; int ans = erfen ( ); printf ( "Case %d: %d ", ++ti, ans ); } }

第一眼看到“最大独立集”,想的完了完了,不会啊怎么办。五分钟后,woc这不就是最长上升子序列吗,好水啊...然后心想这道题班上可能会全a吧,t3要认真才行叻。
结果原来大家都没发现吗...
可以发现每个点到原序列它后面比它小的点都连有一条双向边,要使一个集合里面任意两点都没有连边,在原序列里面这个集合就一定是一个不下降序列。要求最大,那就是最大上升子序列叻...(因为$a[i]$保证不等所以上升就好了
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; int a[100005], dp[100005]; int main ( ) { freopen ( "sort.in", "r", stdin ); freopen ( "sort.out", "w", stdout ); int n; scanf ( "%d", &n ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &a[i] ); memset ( dp, 0x3f3f3f3f, sizeof ( dp ) ); for ( int i = 1; i <= n; i ++ ) { int pos = lower_bound ( dp + 1, dp + 1 + n, a[i] ) - dp; dp[pos] = a[i]; } for ( int i = n; i >= 1; i -- ) if ( dp[i] < 0x3f3f3f3f ) { printf ( "%d", i ); break; } return 0; }

数据明显是状压,可是发现一个状态要存好多东西存不下怎么办!那就多开几个数组呗...
分别储存每个状态红、绿、白钥匙有多少个,每次更新首先保证所有钥匙的和是最大的,其次保证白钥匙数量最多。
然而是很不严谨的...QAQ(但是数据水我们就不在意这些细节叻~
这样会把一些情况给筛掉,导致后面的情况不能进入。
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> using namespace std; int n; int Red[(1<<14)+1], Green[(1<<14)+1], White[(1<<14)+1]; int R[15], G[15], KR[15], KG[15], W[15]; int main ( ) { freopen ( "room.in", "r", stdin ); freopen ( "room.out", "w", stdout ); scanf ( "%d", &n ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &R[i] ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &G[i] ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &KR[i] ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &KG[i] ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &W[i] ); int k0, k1, k2; scanf ( "%d%d%d", &k0, &k1, &k2 ); memset ( Red, -1, sizeof ( Red ) ); memset ( Green, -1, sizeof ( Green ) ); memset ( White, -1, sizeof ( White ) ); Red[0] = k0, Green[0] = k1, White[0] = k2; for ( int i = 0; i < ( 1 << n ); i ++ ) { for ( int j = 1; j <= n; j ++ ) { if ( ! ( ( i >> ( j - 1 ) ) & 1 ) ) { int s = i | ( 1 << ( j - 1 ) ); int wu = max ( G[j] - Green[i], 0 ); if ( wu > White[i] ) continue; if ( Red[i] + ( White[i] - wu ) >= R[j] ) { int pre = Red[i] + Green[i] + White[i] - R[j] - G[j] + KR[j] + KG[j] + W[j]; int now = Red[s] + Green[s] + White[s]; if ( now <= pre ) { int rn = max ( 0, R[j] - Red[i] ), gn = max ( 0, G[j] - Green[i] ); int wn = rn + gn; if ( now == pre && White[s] > White[i] - wn + W[j] ) continue; Red[s] = max ( 0, Red[i] - R[j] ) + KR[j], Green[s] = max ( 0, Green[i] - G[j] ) + KG[j] ; White[s] = White[i] - wn + W[j]; } } } } } int ans = 0; for ( int i = 0; i < ( 1 << n ); i ++ ) ans = max ( ans, Red[i] + Green[i] + White[i] ); printf ( "%d", ans ); return 0; }
正解如下:
#include<cstring> #include<cstdio> #include<iostream> #define fo(i,n) for(int i=0;i<n;i++) using namespace std; const int N=15; int dR[N],dG[N],rR[N],rG[N],rW[N],ky[N],n,f[20000][200],z; int main(){ freopen("room.in","r",stdin); freopen("room.out","w",stdout); cin>>n; fo(i,n) cin>>dR[i]; fo(i,n) cin>>dG[i]; fo(i,n) cin>>rR[i]; fo(i,n) cin>>rG[i]; fo(i,n) cin>>rW[i]; cin>>ky[0]>>ky[1]>>ky[2]; int sum=ky[0]+ky[1]+ky[2]; memset(f,-1,sizeof f); f[0][ky[0]]=ky[2]; fo(i,1<<n){ int k0=ky[0],k1=ky[1],r=sum; fo(j,n) if(i>>j&1){ k0+=rR[j]; r+=rR[j]+rG[j]+rW[j]-dR[j]-dG[j]; } for(int j=0;j<=k0;j++){ if(f[i][j]==-1) continue; int fr=f[i][j]; int k=r-fr-j; fo(l,n){ if(i>>l&1) continue; int r=max(0,dR[l]-j),g=max(0,dG[l]-k); int &q=f[i|(1<<l)][max(0,j-dR[l])+rR[l]]; if(fr>=r+g) q=max(q,fr-r-g+rW[l]); } z=max(z,j+k+fr); } } cout<<z<<endl; }
离$AK$只有清零一步之遥5555555,我还是tclQAQ
抱恨离场QAQ