Catalan数

Catalan数

虽然早就听说了catalan数，但是并不真正理解，昨天做了一个出栈次序的题，学了一下，关于卡特兰数，有很多应用，目前我掌握（说是掌握，也是未必）是出栈次序问题,有n个数，h(n)=C_2nⁿ-C_2n^n-1, 到目前为止，出栈数一定要小于等于入栈数，不然没有进来怎么出去，也就是不合法的方案，现在我们要求合法的方案总数。

折线法证明catalan数

 

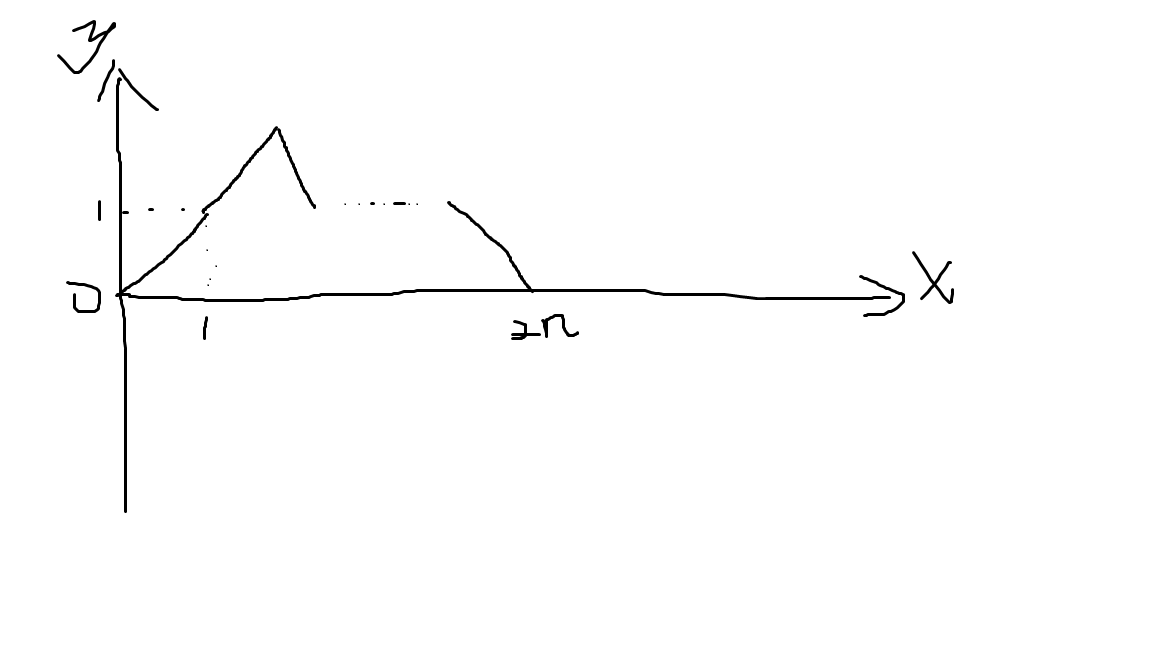
我们假设进栈是向右上方走√2，出栈是向右下方走√2，，经过2n次操作，n个右上，n个右下，一定会走到（2n，0）这个点，整个路径不会跨越x轴就是合法的，否则不合法。

 

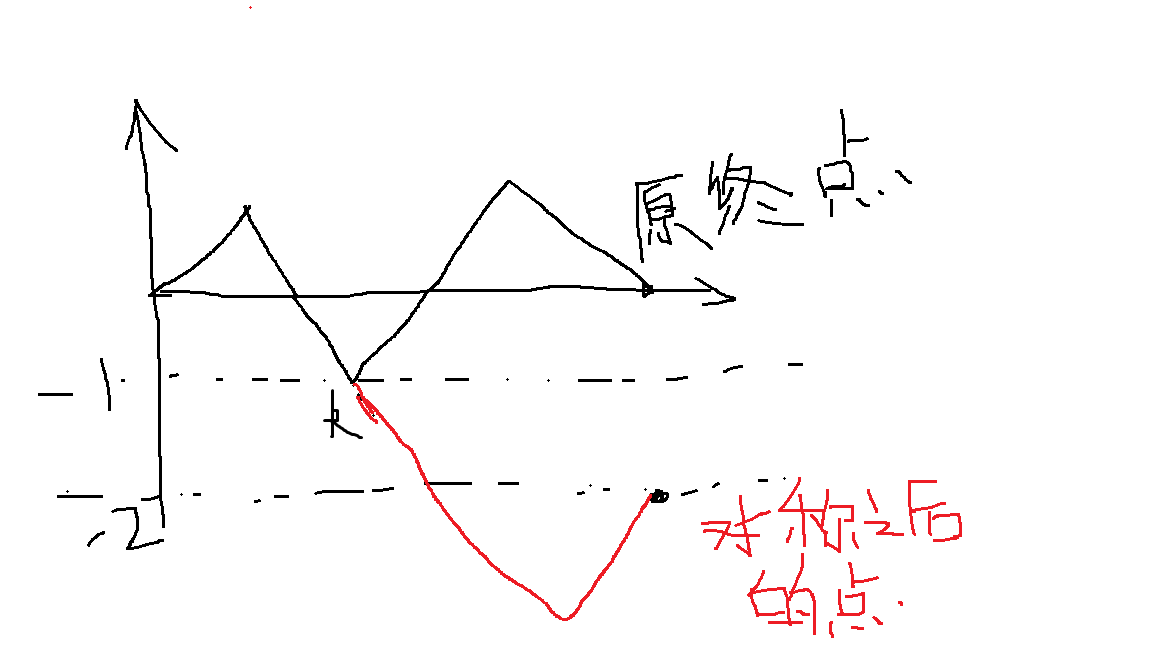
跨越x轴后一定会接触y=-1这条直线，对原路线而言，它一定会再走回去，我对k之后的点关于y=-1进行对称操作，所以一定会跨越y=-1这条直线，终点变成了（2n，-2），所以对于一条不合法的路径而言，就是从（0,0）开始到（2n，-2）结束的路径，在这条路径中，向右下走比向右上走多2步，故往上走了n-1步，下n+1步，不满足的就是C_2n^n-1。

故答案为C_2nⁿ-C_2n^n-1。