回溯法的解空间表示方法

回溯法解题时通常包含3个步骤：

1. 针对所给问题，定义问题的解空间；

2. 确定易于搜索的解空间结构；

3. 以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

对于问题的解空间结构通常以树或图的形式表示，常用的两类典型的解空间树是子集树和排列树。当所给的问题是从n个元素的集合S中找到S满足某种性质的子集时，相应的解空间树称为子集树。例如，n个物品的0-1背包问题所对应的解空间树是一棵子集树，这类子集树通常有2**n个叶结点，遍历子集树的算法需要O(2**n)计算时间。当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。排列树通常有n！个叶结点。因此，排列树需要O(n!)计算时间。当问题的解空间确定后，便可用不同的剪枝函数和最优解表示方法来获得最终结果。下面，介绍用子集树或排列树构造解空间的常见问题。

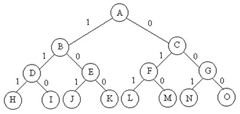
1. 子集树

上图是一棵n=3的子集树。它是一棵完全二叉树（有时可能是n叉树，如图着色问题，每一个结点可能有n种选择），从根到每一个叶结点的路径表示一个可行解。从根结点出发，以深度优先的方式搜索整棵树。用回溯法搜索子集树的一般算法可描述为：

void backtrack(int t)
{
    if(t > n) output(x);
    else
        for(int i = 0; i <= 1; i++) 
        {
            x[t] = i;
            if(constraint(t) && bound(t)) backtrack(t+1);
        }
}

其中，t表示递归深度，表示树的第t层。当t > n时，算法已搜索到叶结点，由output( x ) 输出可行解。否则，记录当前选择的x的值（即0或1），并递归遍历所有子树（这里只有左右子树）。(constraint(t) && bound(t)) 表示剪枝函数，只有满足剪枝函数的子树才继续递归。一棵子集树一共有2**n个可搜索的解，对于所有可用子集树表示解空间的问题都是在这

2**n个解中找到满足条件的解，不同的是剪枝函数不同，最终解的表示形式不同。

1.1 求解组合

给定正整数n和k，求所有k个数的组合，例如，n=4，k=2，解为：

[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

此时，集合S={1,2,3,4}，从第一个元素开始搜索，对于每一个元素可以选择或者不选择，当当前选择到的元素个数等于k时记录这个结果。因此，我们定义result来保存记录的结果，

answer记录了当前选择元素，即当前的解。

class Solution {
public:
    void help(int n , int k , int start, vector<int> &answer, vector<vector<int>> & result) {
        if(k == answer.size()) {
            result.push_back(answer);  //记录结果
            return ;
        }
        if(start > n) return; //搜索至叶结点
        answer.push_back(start);              // 选择当前元素的情况
        help(n, k, start + 1, answer, result);// 
        answer.pop_back();
        help(n, k, start + 1, answer, result);  // 不选择的情况
    }
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> result;
        vector<int> answer;
        help(n, k, 1, answer, result);
        return result;
    }
};

1.2 求解组合和

上面一个问题其实就是在所有S的子集中寻找大小为k的子集，所以最终的解是大小等于k的子集的集合。

现在，我们给定一个整数的集合C，和一个整数T，找到集合C中元素和为T的所有集合的集合。其中，对应每有个C中的元素可以重复多次。

那么，这个问题与上面问题的区别是：1.找到一个解的条件不同（和为T）；2.元素可重复。

class Solution {
private:
    void help(vector<int>& candidates, int start, int target, int sum, vector<int>& answer, vector<vector<int>>& result) {
        if(sum == target) {
            result.push_back(answer);
            return;
        } 
        if(start == candidates.size() || sum + candidates[start] > target) return; // 添加一个剪枝函数，当加入当前元素使和大于T时那么这是一棵不符合条件的子树  
        answer.push_back(candidates[start]);
        help(candidates, start, target, sum + candidates[start], answer, result);//依然从start开始，因为元素可重复
        answer.pop_back();
        help(candidates, start + 1, target, sum, answer, result);
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int> answer;
        vector<vector<int>> result;
        sort(candidates.begin(), candidates.end());
        help(candidates, 0, target, 0, answer, result);
        return result;
    }
};

1.3 求解组合和II

上面一题再变一下，一个元素只能用一次。上面一题为了解决元素可重复的问题，我们遍历的时候，当加入当前元素时，递归遍历继续从当前元素开始。而现在要让元素只被选择一次，那么我们改变搜索策略，当选择当前元素时，我们从下一个元素递归遍历，当没有选择当前元素时，我们需要从下一个与当前不重复的元素开始。

void help(vector<int> & candidates, int start, int sum, int target, vector<int>& answer, vector<vector<int>>& result) {
        if(sum == target) {
            result.push_back(answer);
            return ;
        }
        if(start == candidates.size() || sum + candidates[start] > target) return;
        answer.push_back(candidates[start]);
        help(candidates, start + 1, sum + candidates[start], target, answer, result);
        answer.pop_back();
        while(start + 1 < candidates.size() && candidates[start + 1] == candidates[start]) start++;  //去掉重复的元素
        help(candidates, start + 1, sum, target, answer, result);
    }

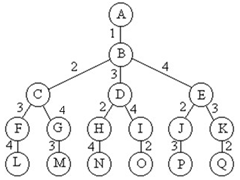
2. 排列树

上图是一棵表示旅行售货员问题的排列树，从根到叶结点表示一条可选路径。与子集树不同的是，每一个当前结点的搜索策略是选择剩下的元素中的一个，而子集树是选择或不选择当前元素。用回溯法搜索排列树的一般算法为：

void backtrack(int t)
{
    if(t > n) output(x);
    else
        for(int i = t; i <= n; i++)  //与子集树不同，搜索剩下的结点
        {
            swap(x[t], x[i]);
            if(constraint(t)&&bound(t)) backtrack(t+1);
            swap(x[t], x[i]);
        }
}

2.1 求排列

For example,
[1,2,3] have the following permutations:
[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], and [3,2,1].

这是一个最简单的排列树搜索问题，因为问题的解就是叶结点个数，即n！个。因此，它没有剪枝函数，只要搜索到叶结点就保存一个解。

class Solution {
private:
    void help(vector<int>& nums, vector<int>& pos, int now, vector<vector<int>>& result) {
        int n = nums.size();
        if(now == n) { //
            vector<int> answer(n, 0);
            for(int i = 0; i < n; i++) {
                answer[i] = nums[pos[i]];  //pos保存元素的下标，这里构造需要的解
            }
            result.push_back(answer);
            return;
        }
        for(int i = now; i < n; i++) {
            swap(pos[now], pos[i]);
            help(nums, pos, now + 1, result);
            swap(pos[now], pos[i]);
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> result;
        int n = nums.size();
        if(n == 0) return result;
        vector<int> pos(n, 0);
        for(int i = 0; i < n; i++) {
            pos[i] = i;
        }
        help(nums, pos, 0, result);
        return result;
    }
};

2.2 n-Queens 问题

n-Queens问题是把n个皇后放在nxn的棋盘上，让她们不能互相攻击。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或者同一斜线上的棋子。一个4皇后问题的解为：

[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

我们可以把问题转换成n个元素的集合的排列问题，而这个排列需要满足上面这个规则。我们按行优先的顺序，从上往下给每一行填一个皇后。这就相当于，解是一个n元向量，向量的元素下标对应于一行行坐标，而元素对应于列坐标。这里为了方便得到最终形式的解，我们把每一个解表示成nxn的char型矩阵。并设置了3个mask用于剪枝函数，即colFlag、

diagFlag1、diagFlag2分别表示列和两对角线的mask，在剪枝函数中只需判断当前位置处这3个mask对应的位是否被置位。

class Solution {
private:
    int colFlag;
    int diagFlag1;
    int diagFlag2;
    bool isValid(int rowIdx, int colIdx, int n) {
        if((1 << colIdx) & colFlag) return false;
        if((1 << (colIdx + rowIdx)) & diagFlag1) return false;
        if((1 << (n + rowIdx - colIdx - 1)) & diagFlag2) return false;
        return true;
    }
    void setFlag(int rowIdx, int colIdx, int n) { //设置mask flag
        colFlag |= (1 << colIdx);
        diagFlag1 |= (1 << (colIdx + rowIdx));
        diagFlag2 |= (1 << (n + rowIdx - colIdx -1));
    }
    void unsetFlag(int rowIdx, int colIdx, int n) { //取消mask flag
        colFlag &= ~(1 << colIdx);
        diagFlag1 &= ~(1 << (colIdx + rowIdx));
        diagFlag2 &= ~(1 << (n + rowIdx - colIdx -1));
    }
    void help(int n, vector<string>& answer, vector<vector<string>>& result) {
        int rowIdx = answer.size();
        if(rowIdx == n) { //搜索完成，记录结果
            result.push_back(answer);
            return;
        }
        answer.push_back(string(n,'.'));
        for(int i = 0; i < n; ++i) {
            if(isValid(rowIdx, i, n)) { //如果当前位置可用
                setFlag(rowIdx, i, n); //设置flag表示选择了
                answer.back()[i] = 'Q';
                help(n, answer, result);
                answer.back()[i] = '.';
                unsetFlag(rowIdx, i, n);//取消flag，回溯
            }
        }
        answer.pop_back();
    }
public:
    vector<vector<string> > solveNQueens(int n) {
        colFlag = diagFlag1 = diagFlag2 = 0;
        vector<string> answer;
        vector<vector<string>> result;
        help(n, answer, result);
        return result;
    }
};

总结：

子集树和排列树的不同是每一步的选择策略不同。子集树每一步对应的是对应的元素的选择或不选择，排列树每一步对应的是剩下的元素选择其中一个。一个的可搜索的解为2**n，一个为n！，因此，一个高效的回溯法算法必须依赖于剪枝函数来避免无效搜索。

参考资料

1.《算法设计与分析（第二版）》 清华大学出版社

2. leetcode.com

作者：waring  出处：http://www.cnblogs.com/waring  欢迎转载或分享，但请务必声明文章出处。