P3979 遥远的国度(树剖换根)

树剖的换根分析

(先以1为根建树)在求换根后的(x)的子树的相关信息(最小值为例)时，我们可以这样考虑：

​ 如果现在的根为(r)，当我输入查询(x)的子树分为以下几种情况：

1 .(x==r)，此时我们要查询的子树的最小值(以(r)为根)就是以1为根时的全局最小值

2 .当(xquad r)的(LCA)是(x)时，此时我们可以从图上直观的看出，我们要求的(x)的子树上的最小值其实就是去掉((x)和(r)这条路上的(x)的儿子 的子树)相关区域，剩下的即为求。

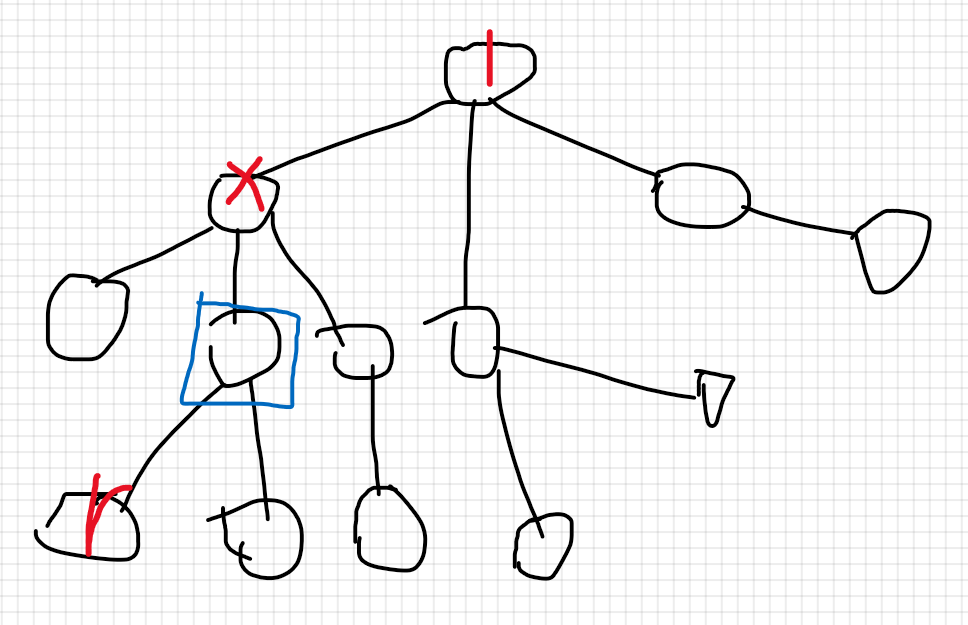
if(LCA(x, r) == x && dep[r] > dep[x]) {
    int y = LCA_son(x, r);
    if(id[y] + sz[y] <= n) {
        printf("%lld
", min(s_t.query(1, 1, n, 1, id[y] - 1), s_t.query(1, 1, n, id[y] + sz[y], n)));
    } else
        printf("%lld
", s_t.query(1, 1, n, 1, id[y] - 1));
} else {
    printf("%lld
", query_son(x));
}

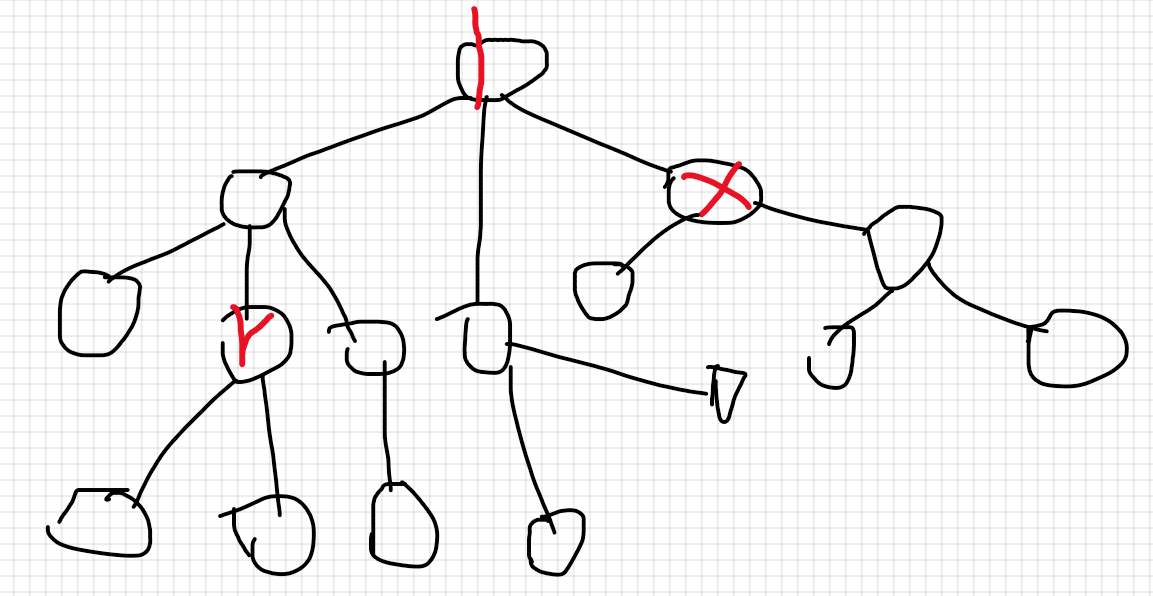
3 .当(r，x)的(LCA)不是(x)时，观察图我们可以看出，还是本来(x)自己的子树，直接查询即可。

P3979 遥远的国度

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define DOF 0x7f7f7f7f
#define endl '
'
#define mem(a, b) memset(a, b, sizeof(a))
#define debug(case, x) cout << case << "  : " << x << endl
#define open freopen("ii.txt", "r", stdin)
#define close freopen("oo.txt", "w", stdout)
#define IO                       
    ios::sync_with_stdio(false); 
    cin.tie(0);                  
    cout.tie(0)
#define pb push_back
using namespace std;
#define int long long
#define lson rt << 1
#define rson rt << 1 | 1
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<long long, long long> PII;
const int maxn = 1e5 + 10;

int n, m, r;

int head[maxn], tot;
struct edge {
    int to, next;
} edge[maxn << 1];

int w[maxn], wt[maxn];
//w输入时的权值，wt编号后的权值

int son[maxn], id[maxn], fa[maxn], dep[maxn], sz[maxn], top[maxn], cnt = 0;
//son重儿子、id新编号、fa父亲节点、dep深度、sz子树大小、top顶端、cnt标号。

void add(int u, int v) {
    edge[++tot].to = v;
    edge[tot].next = head[u];
    head[u] = tot;
}

struct SegTree {
    int tree[maxn << 2], lazy[maxn << 2];

    void push_down(int rt, int len) {
        if(lazy[rt]) {
            lazy[lson] = lazy[rt];
            lazy[rson] = lazy[rt];
            tree[lson] = lazy[rt];
            tree[rson] = lazy[rt];
//            tree[lson] %= mod;
//            tree[rson] %= mod;
            lazy[rt] = 0;
        }

    }

    void push_up(int rt) {
        tree[rt] = min(tree[lson], tree[rson]);
    }

    void build(int rt, int l, int r) {
        if(l == r) {
            tree[rt] = wt[l];
//            tree[rt] %=  mod;
            return ;
        }
        int mid = (l + r) >> 1;
        build(lson, l, mid);
        build(rson, mid + 1, r);

        push_up(rt);
//        tree[rt]=min(tree[lson],tree[rson]);
//        tree[rt] = (tree[lson] + tree[rson]) % mod;
    }

    int query(int rt, int l, int r, int L, int R) {
        if(L <= l && r <= R) {
            return tree[rt];
        }
        push_down(rt, r - l + 1);
        int mid = (l + r) >> 1, res = 1e18;
        if(L <= mid)
            res = min(res, query(lson, l, mid, L, R));
        if(R > mid)
            res = min(res, query(rson, mid + 1, r, L, R));
        return res;
    }

    void update(int rt, int l, int r, int L, int R, int k) {
        if(L <= l && r <= R) {
            lazy[rt] = k;
            tree[rt] = k;
            return ;
        }
        push_down(rt, r - l + 1);
        int mid = (l + r) >> 1;

        if(L <= mid)
            update(lson, l, mid, L, R, k);
        if(R > mid)
            update(rson, mid + 1, r, L, R, k);
        push_up(rt);
    }
} s_t;


void dfs1(int u, int father) {
    dep[u] = dep[father] + 1;
    sz[u] = 1;
    fa[u] = father;
    int maxson = -1;
    for(int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].to;
        if(v == father)continue;
        dfs1(v, u);
        sz[u] += sz[v];
        if(sz[v] > maxson)
            son[u] = v, maxson = sz[v];
    }

}

void dfs2(int u, int topf) {
    id[u] = ++cnt;
    wt[cnt] = w[u];
    top[u] = topf;
    if(!son[u]) return ;
    dfs2(son[u], topf);
    for(int i = head[u]; i; i = edge[i].next) {
        int v = edge[i].to;
        if(v == fa[u] || v == son[u]) continue;
        dfs2(v, v);
    }

}


int query(int x, int y) {
    int res = 1e9;
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]])swap(x, y);
        res = min(res, s_t.query(1, 1, n, id[top[x]], id[x]));
//        res %= mod;
        x = fa[top[x]];
    }
    if(dep[x] > dep[y])swap(x, y);
    res = min(res, s_t.query(1, 1, n, id[x], id[y]));
//    res %= mod;
    return res;
}

void update(int x, int y, int k) {
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]])swap(x, y);
        s_t.update(1, 1, n, id[top[x]], id[x], k);
        x = fa[top[x]];
    }
    if(dep[x] > dep[y])swap(x, y);
    s_t.update(1, 1, n, id[x], id[y], k);

}

int query_son(int x) {
    return s_t.query(1, 1, n, id[x], id[x] + sz[x] - 1);
}

void update_son(int x, int k) {
    s_t.update(1, 1, n, id[x], id[x] + sz[x] - 1, k);

}



int LCA(int x, int y) {
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]])swap(x, y);
        x = fa[top[x]];
    }
    return dep[x] < dep[y] ? x : y;

}

int LCA_son(int x, int y) {//取得高处的那个节点在root方向上的儿子
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]])swap(x, y);
        if(fa[top[x]] == y)return top[x];
        x = fa[top[x]];
    }
    if(dep[x] > dep[y])swap(x, y);
    return son[x];

}


signed main() {
    scanf("%lld%lld", &n, &m);
    for(int i = 1; i < n; ++i) {
        int x, y;
        scanf("%lld%lld", &x, &y);
        add(x, y);
        add(y, x);
    }
    for(int i = 1; i <= n; ++i)scanf("%lld", &w[i]);
    scanf("%lld", &r);
    dfs1(1, 0);
    dfs2(1, 1);
    s_t.build(1, 1, n);

    while(m--) {
        int opt, idx, x, y, v;
        scanf("%lld", &opt);
        if(opt == 1) {
            scanf("%lld", &idx);
            r = idx;
        } else if(opt == 2) {
            scanf("%lld%lld%lld", &x, &y, &v);
            update(x, y, v);
        } else {
            scanf("%lld", &x);
            if(x == r)
                printf("%lld
", s_t.tree[1]);
            else if(LCA(x, r) == x && dep[r] > dep[x]) {
                int y = LCA_son(x, r);
                if(id[y] + sz[y] <= n) {
                    printf("%lld
", min(s_t.query(1, 1, n, 1, id[y] - 1), s_t.query(1, 1, n, id[y] + sz[y], n)));
                } else
                    printf("%lld
", s_t.query(1, 1, n, 1, id[y] - 1));
            } else {
                printf("%lld
", query_son(x));
            }
        }
    }
}