通过源码分析朴素贝叶斯
手写朴素贝叶斯源码
1 from numpy import * 2 from functools import reduce 3 4 # 广告、垃圾标识 5 adClass = 1 6 7 8 def loadDataSet(): 9 """加载数据集合及其对应的分类""" 10 wordsList = [['周六', '公司', '一起', '聚餐', '时间'], 11 ['优惠', '返利', '打折', '优惠', '金融', '理财'], 12 ['喜欢', '机器学习', '一起', '研究', '欢迎', '贝叶斯', '算法', '公式'], 13 ['公司', '发票', '税点', '优惠', '增值税', '打折'], 14 ['北京', '今天', '雾霾', '不宜', '外出', '时间', '在家', '讨论', '学习'], 15 ['招聘', '兼职', '日薪', '保险', '返利']] 16 # 1 是, 0 否 17 classVec = [0, 1, 0, 1, 0, 1] 18 return wordsList, classVec 19 20 21 # python中的& | 是位运算符 and or是逻辑运算符 当and的运算结果为true时候返回的并不是true而是运算结果最后一位变量的值 22 # 当and返回的结果是false时候,如果A AND B 返回的是第一个false的值,如果a为false 则返回a,如果a不是false,那么返回b 23 # 如果a or b 为true时候,返回的是第一个真的变量的值,如果a,b都为真时候那么返回a 如果a为假b为真那么返回b 24 # a & b a和b为两个set,返回结果取a和b的交集 a|b a和b为两个set,返回结果为两个集合的不重复并集 25 def doc2VecList(docList): 26 # 从第一个和第二个集合开始进行并集操作,最后返回一个不重复的并集 27 a = list(reduce(lambda x, y: set(x) | set(y), docList)) 28 return a 29 30 31 def words2Vec(vecList, inputWords): 32 """把单子转化为词向量""" 33 # 转化成以一维数组 34 resultVec = [0] * len(vecList) 35 for word in inputWords: 36 if word in vecList: 37 # 在单词出现的位置上的计数加1 38 resultVec[vecList.index(word)] += 1 39 else: 40 print('没有发现此单词') 41 42 return array(resultVec) 43 44 45 def trainNB(trainMatrix, trainClass): 46 """计算,生成每个词对于类别上的概率""" 47 # 类别行数 48 numTrainClass = len(trainClass) 49 # 列数 50 numWords = len(trainMatrix[0]) 51 52 # 全部都初始化为1, 防止出现概率为0的情况出现 53 # 见于韩家炜的数据挖掘概念与技术上的讲解,避免出现概率为0的状况,影响计算,因为在数量很大的情况下,在分子和分母同时+1的情况不会 54 # 影响主要的数据 55 p0Num = ones(numWords) 56 p1Num = ones(numWords) 57 # 相应的单词初始化为2 58 # 为了分子分母同时都加上某个数λ 59 p0Words = 2.0 60 p1Words = 2.0 61 # 统计每个分类的词的总数 62 # 训练数据集的行数作为遍历的条件,从1开始 63 # 如果当前类别为1,那么p1Num会加上当前单词矩阵行数据,依次遍历 64 # 如果当前类别为0,那么p0Num会加上当前单词矩阵行数据,依次遍历 65 # 同时统计当前类别下单词的个数和p1Words和p0Words 66 for i in range(numTrainClass): 67 if trainClass[i] == 1: 68 # 数组在对应的位置上相加 69 p1Num += trainMatrix[i] 70 p1Words += sum(trainMatrix[i]) 71 else: 72 p0Num += trainMatrix[i] 73 p0Words += sum(trainMatrix[i]) 74 # 计算每种类型里面, 每个单词出现的概率 75 # 朴素贝叶斯分类中,y=x是单调递增函数,y=ln(x)也是单调的递增的 76 # 如果x1>x2 那么ln(x1)>ln(x2) 77 # 在计算过程中,由于概率的值较小,所以我们就取对数进行比较,根据对数的特性 78 # ln(MN) = ln(M)+ln(N) 79 # ln(M/N) = ln(M)-ln(N) 80 # ln(M**n)= nln(M) 81 # 注:其中ln可替换为log的任意对数底 82 p0Vec = log(p0Num / p0Words) 83 p1Vec = log(p1Num / p1Words) 84 # 计算在类别中1出现的概率,0出现的概率可通过1-p得到 85 pClass1 = sum(trainClass) / float(numTrainClass) 86 return p0Vec, p1Vec, pClass1 87 88 89 def classifyNB(testVec, p0Vec, p1Vec, pClass1): 90 # 朴素贝叶斯分类, max(p0, p1)作为推断的分类 91 # y=x 是单调递增的, y=ln(x)也是单调递增的。 , 如果x1 > x2, 那么ln(x1) > ln(x2) 92 # 因为概率的值太小了,所以我们可以取ln, 根据对数特性ln(ab) = lna + lnb, 可以简化计算 93 # sum是numpy的函数,testVec是一个数组向量,p1Vec是一个1的概率向量,通过矩阵之间的乘机 94 # 获得p(X1|Yj)*p(X2|Yj)*...*p(Xn|Yj)*p(Yj) 95 # 其中pClass1即为p(Yj) 96 # 此处计算出的p1是用对数表示,按照上面所说的,对数也是单调的,而贝叶斯分类主要是通过比较概率 97 # 出现的大小,不需要确切的概率数据,因此下述表述完全正确 98 p1 = sum(testVec * p1Vec) + log(pClass1) 99 p0 = sum(testVec * p0Vec) + log(1 - pClass1) 100 if p0 > p1: 101 return 0 102 return 1 103 104 105 def printClass(words, testClass): 106 if testClass == adClass: 107 print(words, '推测为:广告邮件') 108 else: 109 print(words, '推测为:正常邮件') 110 111 112 def tNB(): 113 # 从训练数据集中提取出属性矩阵和分类数据 114 docList, classVec = loadDataSet() 115 # 生成包含所有单词的list 116 # 此处生成的单词向量是不重复的 117 allWordsVec = doc2VecList(docList) 118 # 构建词向量矩阵 119 # 计算docList数据集中每一行每个单词出现的次数,其中返回的trainMat是一个数组的数组 120 trainMat = list(map(lambda x: words2Vec(allWordsVec, x), docList)) 121 # 训练计算每个词在分类上的概率, p0V:每个单词在非分类出现的概率, p1V:每个单词在是分类出现的概率 122 # 其中概率是以ln进行计算的 123 # pClass1为类别中是1的概率 124 p0V, p1V, pClass1 = trainNB(trainMat, classVec) 125 # 测试数据集 126 testWords = ['公司', '聚餐', '讨论', '贝叶斯'] 127 # 转换成单词向量,32个单词构成的数组,如果此单词在数组中,数组的项值置1 128 testVec = words2Vec(allWordsVec, testWords) 129 # 通过将单词向量testVec代入,根据贝叶斯公式,比较各个类别的后验概率,判断当前数据的分类情况 130 testClass = classifyNB(testVec, p0V, p1V, pClass1) 131 # 打印出测试结果 132 printClass(testWords, testClass) 133 134 testWords = ['公司', '保险', '金融'] 135 # 转换成单词向量,32个单词构成的数组,如果此单词在数组中,数组的项值置1 136 testVec = words2Vec(allWordsVec, testWords) 137 # 通过将单词向量testVec代入,根据贝叶斯公式,比较各个类别的后验概率,判断当前数据的分类情况 138 testClass = classifyNB(testVec, p0V, p1V, pClass1) 139 # 打印出测试结果 140 printClass(testWords, testClass) 141 142 143 if __name__ == '__main__': 144 tNB()
源码拆解分析
1、训练数据集的加载
数据包括特征列和标签
1 def loadDataSet(): 2 """加载数据集合及其对应的分类""" 3 wordsList = [['周六', '公司', '一起', '聚餐', '时间'], 4 ['优惠', '返利', '打折', '优惠', '金融', '理财'], 5 ['喜欢', '机器学习', '一起', '研究', '欢迎', '贝叶斯', '算法', '公式'], 6 ['公司', '发票', '税点', '优惠', '增值税', '打折'], 7 ['北京', '今天', '雾霾', '不宜', '外出', '时间', '在家', '讨论', '学习'], 8 ['招聘', '兼职', '日薪', '保险', '返利']] 9 # 1 是, 0 否 10 classVec = [0, 1, 0, 1, 0, 1] 11 return wordsList, classVec
2、制作所有词的一个列表
注意:这里有一个小技巧:合并俩个list中的所有不重复元素的方法可以使用位运算符--|
list(reduce(lambda x, y: set(x) | set(y), docList))
1 def doc2VecList(docList): 2 # 从第一个和第二个集合开始进行并集操作,最后返回一个不重复的并集 3 a = list(reduce(lambda x, y: set(x) | set(y), docList)) 4 return a
3、制作类似one-hot的矩阵,在单词出现位置的是出现的次数
1 def words2Vec(vecList, inputWords): 2 """把单子转化为词向量""" 3 # 转化成以一维数组 4 resultVec = [0] * len(vecList) 5 for word in inputWords: 6 if word in vecList: 7 # 在单词出现的位置上的计数加1 8 resultVec[vecList.index(word)] += 1 9 else: 10 print('没有发现此单词') 11 12 return array(resultVec)
4、核心代码:训练朴素贝叶斯
1 def trainNB(trainMatrix, trainClass): 2 """计算,生成每个词对于类别上的概率""" 3 # 类别行数 4 numTrainClass = len(trainClass) 5 # 列数 6 numWords = len(trainMatrix[0]) 7 8 # 全部都初始化为1, 防止出现概率为0的情况出现 9 # 见于韩家炜的数据挖掘概念与技术上的讲解,避免出现概率为0的状况,影响计算,因为在数量很大的情况下,在分子和分母同时+1的情况不会 10 # 影响主要的数据 11 p0Num = ones(numWords) 12 p1Num = ones(numWords) 13 # 相应的单词初始化为2 14 # 为了分子分母同时都加上某个数λ 15 p0Words = 2.0 16 p1Words = 2.0 17 # 统计每个分类的词的总数 18 # 训练数据集的行数作为遍历的条件,从1开始 19 # 如果当前类别为1,那么p1Num会加上当前单词矩阵行数据,依次遍历 20 # 如果当前类别为0,那么p0Num会加上当前单词矩阵行数据,依次遍历 21 # 同时统计当前类别下单词的个数和p1Words和p0Words 22 for i in range(numTrainClass): 23 if trainClass[i] == 1: 24 # 数组在对应的位置上相加 25 p1Num += trainMatrix[i] 26 p1Words += sum(trainMatrix[i]) 27 else: 28 p0Num += trainMatrix[i] 29 p0Words += sum(trainMatrix[i]) 30 # 计算每种类型里面, 每个单词出现的概率 31 # 朴素贝叶斯分类中,y=x是单调递增函数,y=ln(x)也是单调的递增的 32 # 如果x1>x2 那么ln(x1)>ln(x2) 33 # 在计算过程中,由于概率的值较小,所以我们就取对数进行比较,根据对数的特性 34 # ln(MN) = ln(M)+ln(N) 35 # ln(M/N) = ln(M)-ln(N) 36 # ln(M**n)= nln(M) 37 # 注:其中ln可替换为log的任意对数底 38 p0Vec = log(p0Num / p0Words) 39 p1Vec = log(p1Num / p1Words) 40 # 计算在类别中1出现的概率,0出现的概率可通过1-p得到 41 pClass1 = sum(trainClass) / float(numTrainClass) 42 return p0Vec, p1Vec, pClass1
其实上面做的就是统计计数工作,最终计算我们需要的概率
- 统计类别数--计算p(嫁) or p(不嫁)
- numTrainClass = len(trainClass)
- 统计所有的特征的总数
- numWords = len(trainMatrix[0])
- 避免出现概率为0的状况,影响计算,因为在数量很大的情况下,在分子和分母同时+1的情况不会影响主要的数据
- p0Num = ones(numWords)
- p1Num = ones(numWords)
- 单词初始化为2,为了分子分母同时都加上某个数λ
- p0Words = 2.0
- p1Words = 2.0
- 同时统计当前类别下单词的个数和p1Words和p0Words (这个部分实际上就是在统计每个类别在的单词的数量,用于计算)
-
1 for i in range(numTrainClass): 2 if trainClass[i] == 1: 3 # 数组在对应的位置上相加 4 p1Num += trainMatrix[i] 5 p1Words += sum(trainMatrix[i]) 6 else: 7 p0Num += trainMatrix[i] 8 p0Words += sum(trainMatrix[i])
- 计算每一个词在该类别下的概率,实际上这个位置是矩阵的运算(对应元素之间的计算),p0Words是类别零中的所有单词的数量,p0Num 是一个计数矩阵,例子:[开心,哈哈,嘻嘻,蹦蹦,跳跳],p0Num [1,2,1,3,2] ,p0Words = 1+2+1+3+2=9,p0Vec = log([1/9,2/9,1/9,3/9,2/9]) log运算是为了下面的计算
- p0Vec = log(p0Num / p0Words)
- p1Vec = log(p1Num / p1Words)
- 计算一个类别的概率:P(嫁) 则P(不嫁)=1-P(嫁)
- pClass1 = sum(trainClass) / float(numTrainClass)
- 最终的返回值实际上就是上一篇blog中可求的三个量
- p0Vec, p1Vec, pClass1
5.预测过程:分类
1 def classifyNB(testVec, p0Vec, p1Vec, pClass1): 2 # 朴素贝叶斯分类, max(p0, p1)作为推断的分类 3 # y=x 是单调递增的, y=ln(x)也是单调递增的。 , 如果x1 > x2, 那么ln(x1) > ln(x2) 4 # 因为概率的值太小了,所以我们可以取ln, 根据对数特性ln(ab) = lna + lnb, 可以简化计算 5 # sum是numpy的函数,testVec是一个数组向量,p1Vec是一个1的概率向量,通过矩阵之间的乘机 6 # 获得p(X1|Yj)*p(X2|Yj)*...*p(Xn|Yj)*p(Yj) 7 # 其中pClass1即为p(Yj) 8 # 此处计算出的p1是用对数表示,按照上面所说的,对数也是单调的,而贝叶斯分类主要是通过比较概率 9 # 出现的大小,不需要确切的概率数据,因此下述表述完全正确 10 p1 = sum(testVec * p1Vec) + log(pClass1) 11 p0 = sum(testVec * p0Vec) + log(1 - pClass1) 12 if p0 > p1: 13 return 0 14 return 1
核心的代码就是计算概率,最终根据概率的大小决定分类:
- 对于原始公式的一个说明:
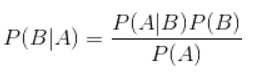
- 在这里对于类别1和类别0的P(A)是相同的,所以不计算也不影响结果
- P(B|A) 等价于P(A|B)*P(B) 取log运算 log(P(B|A))~ log(P(A|B)) + log(B) ~ i 从1到allwords sum(log(P(Ai|B))) + log(B)
- 代码 p1 = sum(testVec * p1Vec) + log(pClass1) 前面的sum(testVec * p1Vec) 向量计算就是在计算P(A|B) ,后面的log(pClass1)就是计算log(B)
- 最终计算得到p0和p1的概率,比较就可以做出分类
- 对上面的预测的计算过程进行简单理解
- 我们在训练过程中,就会得到一个关于allwords中各个词对于不同类别之间的一个贡献向量,表明各个词对类别的贡献程度
- 测试过程中我们统计了一个样本的allwords的词语个数的一个向量,和我们之前准备好的贡献向量相乘,再加上一个类别的概率,就会将测试文本属于各个类别的概率计算出来
- 比较各个类别概率的大小,就完成了分类的过程
6.最终的结果展示:
1 ['公司', '聚餐', '讨论', '贝叶斯'] 推测为:正常邮件 2 ['公司', '保险', '金融'] 推测为:广告邮件