我的策略
我想法是利用循环数组打印杨辉三角,事先通过PPT资料了解到要想打印n行的杨辉三角那么数组的长度就应该定义为(n+2)。老师给的资料中有一个演示了杨辉三角的打印过程,但不完全。其中涉及到一个问题“初始定义”
打印5行数,数组的长度应该定义为7.那么初始的值应该设置为:index[0]=0,index[1]=1,index[2]=0;
利用双循环来打印,第一层循环是层数,第二层循环是每层的元素。这里出现了一个问题:第二层循环的第一次应该循环几次?按照一般思路来说,n层那么第二层打印元素的循环就应该按照1.2.3.4...递增。但是却出现如下问题:
 于是我单步跟踪了一下:
于是我单步跟踪了一下: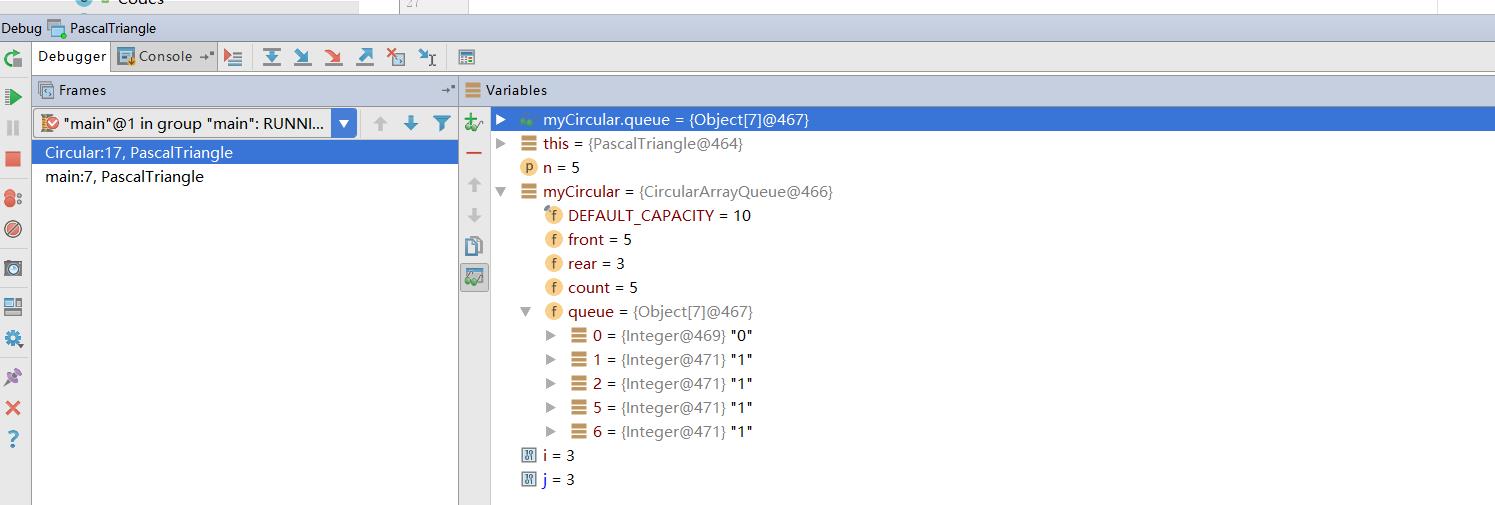
动手画出的图表明在外层循环到第三次也就是打印第三层“1 2 1”时出现了差错,分析表明,其实一开始就已经出错了,能打印出一二层是因为巧合的原因。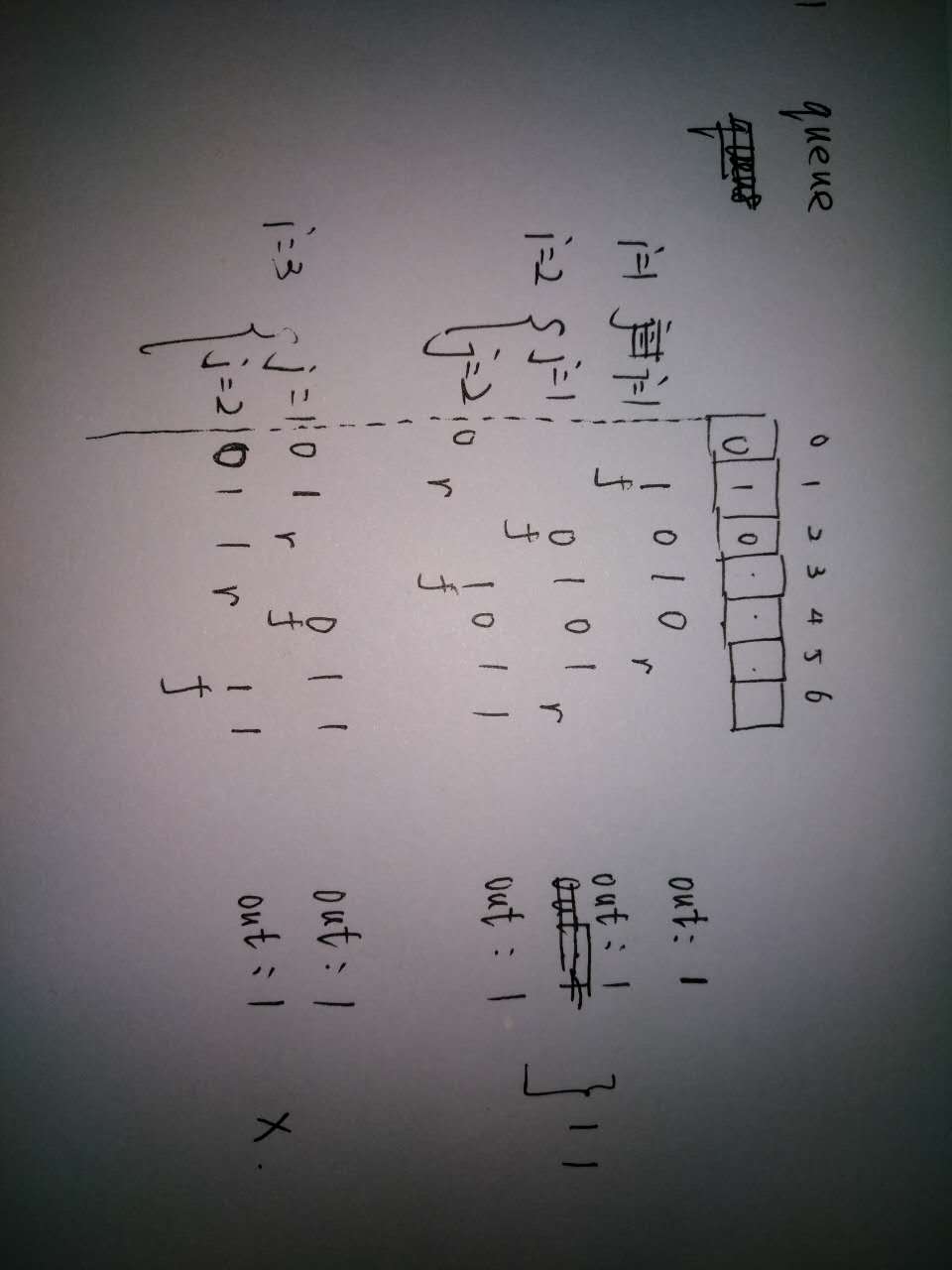
根据自己的思路内层循环每次都会先有出列再入列的操作,所以每层的打印后正确的队列变化应该是: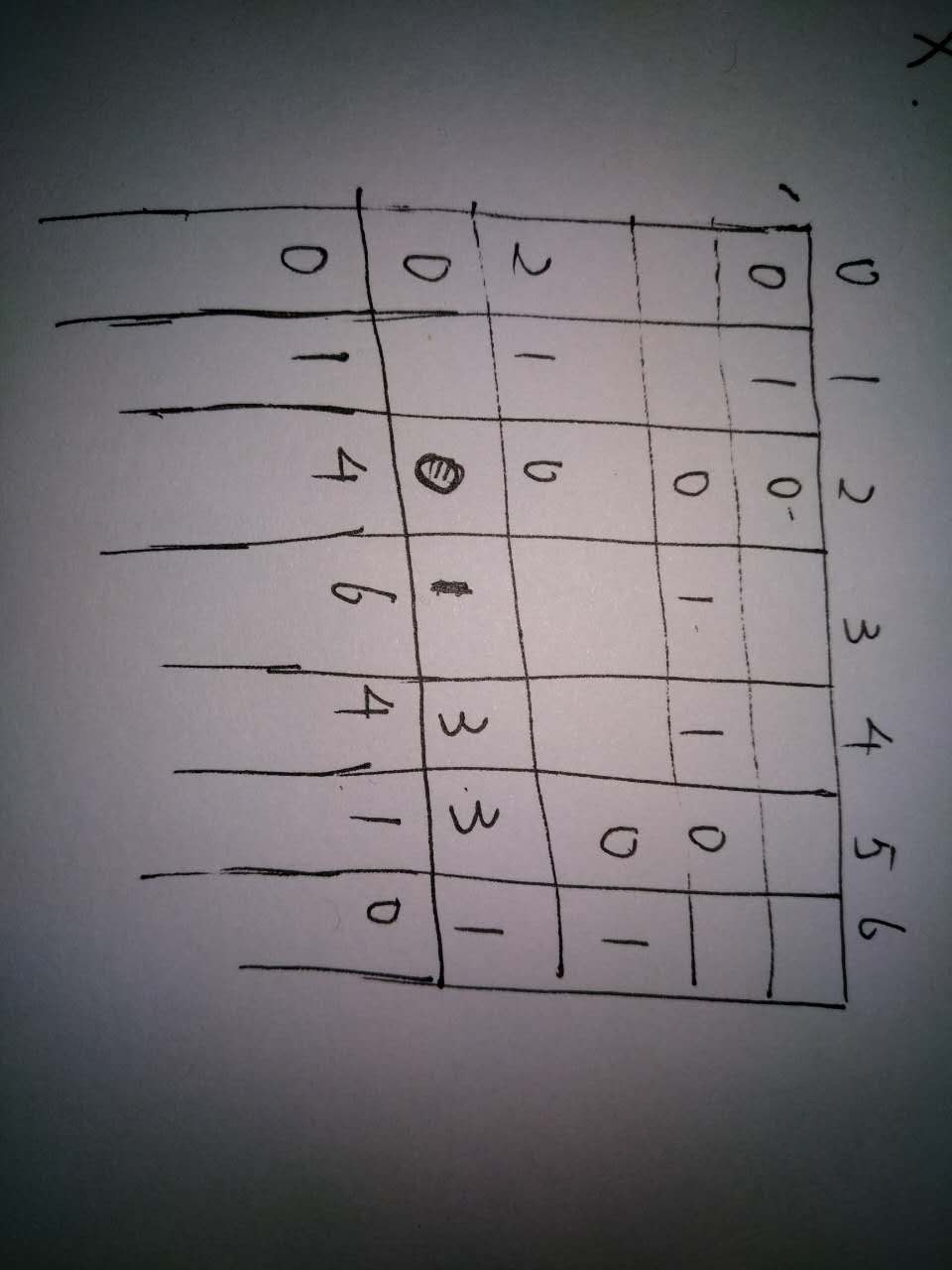
所以我修改了内层打印的次数,在一开始便直接打印出首层的“1”: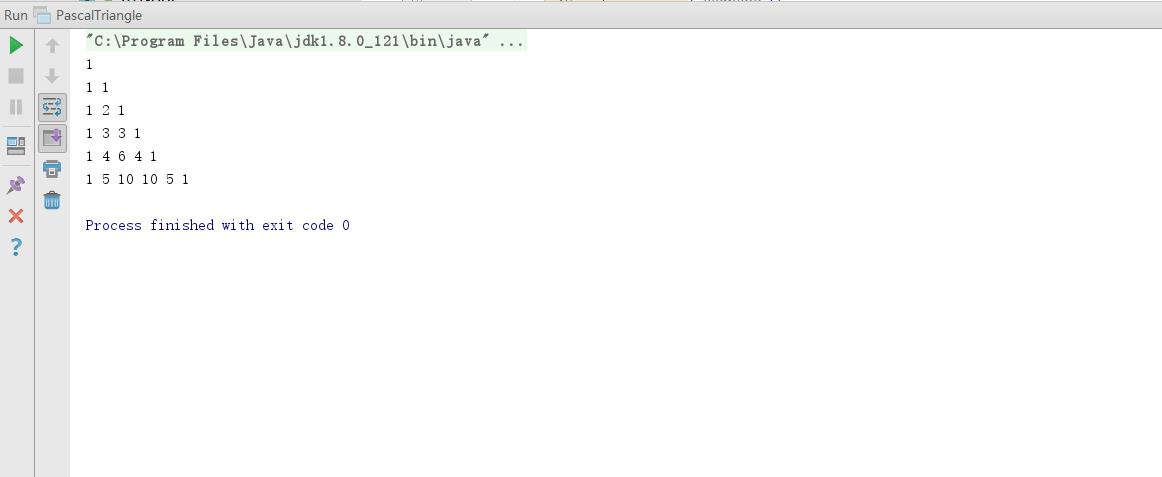
我的代码
public class PascalTriangle {
public static void main(String[] args) {
PascalTriangle myPascal = new PascalTriangle();
myPascal.Circular(5);
}
public void Circular(int n){
CircularArrayQueue myCircular = new CircularArrayQueue(n+2);
myCircular.enqueue(0);
myCircular.enqueue(1);
myCircular.enqueue(0);
System.out.print(1+" "+"
");
for (int i=1;i<=n;i++){
for (int j=1;j<=i+1;j++){
int first = (int)myCircular.dequeue();
int second = (int)myCircular.first();
int num = first+second;
myCircular.enqueue(num);
System.out.print(num+" ");
}
myCircular.enqueue(0);
System.out.print("
");
}
}
}
感想:这个程序看似代码很少,但其中也走了不少弯路,例如在开始时单纯的根据视频资料上面来处理,并没有考虑到先出列的操作,并且在后面补0的操作,于是想的是在每次打印出一层的元素后,重新定义一个数组以0为第一个元素再插入上一行打印的元素再在最后插入0,显得十分的复杂,中途就放弃了这种数据结构。总之这次实验也是学到了不少,再写这边博客时,关于用计算链在数组中表示二叉树出现了点状况,顿时感觉“革命尚未成功,同志人需努力”