王彪-20162321《程序设计与数据结构2nd》-第十一周学习总结与实验报告

邻接矩阵实现

例图

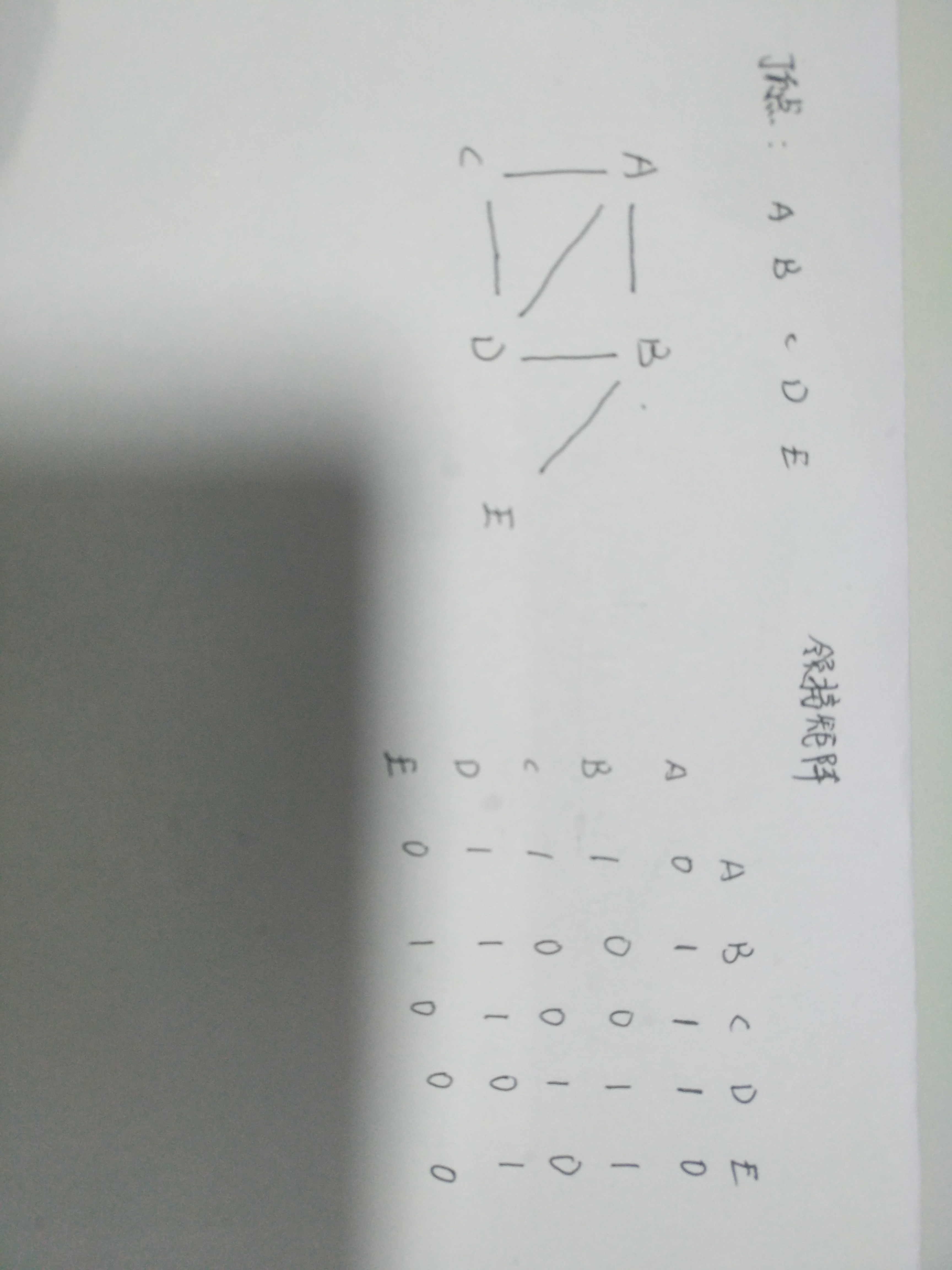
分析

变量

• 需要一个链表来保存数据-即保存结点
• 需要一个二维数组来保存每个变得权值，有则填入具体数值，没有则用0
• 定义一个保存边个数的值

函数方法

• 得到图中边的个数
• 得到结点的数据
• 得到具体边的权值
• 插入结点，删除节点
• 插入边，删除边
• isEmpty，size
• 广度优先遍历，深度优先遍历

具体实践

• 插入,删除结点与边
  我认为邻接矩阵的变换是根据结点来变化的。所以我先定义了构造函数它传入参数n,作为初始值，用来帮助实例化结点链表和二维数组。

    public AMgroup (int n){
        edges = new int [n][n];
        myList = new ArrayList<>(n);
        NumEdges = 0;
        room = n;
    }

插入结点并不改变二维数组本身，除非插入的结点个数大于初始参数n;但删除结点时就不得不考虑由于结点remove导致二维数组中该节点参与的横和列都不能填入值，0也不可以，应该移除此横和列，重新定义新的数组。

    public void helpRemoveEdges(T item){
        int position = myList.indexOf(item);
        int[][] Newedge = new int[room-1][room-1];
        for (int i=0;i<room;i++){
            if (i==position){
                continue;
            }
            if (i<position){
                for (int j=0;j<room;j++){
                    if (j==position)
                        continue;
                    if (j<position)
                        Newedge[i][j]=edges[i][j];
                    if (j>position)
                        Newedge[i][j-1]=edges[i][j];
                }
            }
            if (i>position){
                for (int j=0;j<room;j++){
                    if (j==position)
                        continue;
                    if (j<position)
                        Newedge[i-1][j]=edges[i][j];
                    if (j>position)
                        Newedge[i-1][j-1]=edges[i][j];
                }
            }
        }
        edges = Newedge;
    }

• 插入删除的具体代码

    public void insertEdge(int x,int y,int weight){
        edges[x][y]=weight;
        NumEdges++;
    }
    public void removeEdge(int x,int y){
        edges[x][y]=0;
        NumEdges--;
    }
    public void insertNode(T item){
        myList.add(item);
    }
    public void removeNode(T item){
        helpRemoveEdges(item);
        myList.remove(item);
    }

• 深度优先遍历

1.访问初始结点v，并标记结点v为已访问。
2.查找结点v的第一个邻接结点w。
3.若w存在，则继续执行4，否则算法结束。
4.若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
5.查找结点v的w邻接结点的下一个邻接结点，转到步骤3