摘自:https://www.captainbed.net/2018/11/18/whatisnn/
神经网络
人工神经网络是受到人类大脑结构的启发而创造出来的,在我们的大脑中,有数十亿个称为神经元的细胞,它们连接成了一个神经网络。
人工神经网络正是模仿了上面的网络结构。下面是一个人工神经网络的构造图。每一个圆代表着一个神经元,他们连接起来构成了一个网络。

人类大脑神经元细胞的树突接收来自外部的多个强度不同的刺激,并在神经元细胞体内进行处理,然后将其转化为一个输出结果。如下图所示。

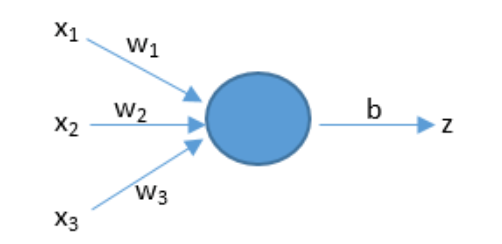
人工神经元也有相似的工作原理。如下图所示。

上面的x是神经元的输入,相当于树突接收的多个外部刺激。w是每个输入对应的权重,它影响着每个输入x的刺激强度。
大脑的结构越简单,那么智商就越低。单细胞生物是智商最低的了。人工神经网络也是一样的,网络越复杂它就越强大,所以我们需要深度神经网络。这里的深度是指层数多,层数越多那么构造的神经网络就越复杂。
训练深度神经网络的过程就叫做深度学习。
网络构建好了后,我们只需要负责不停地将训练数据输入到神经网络中,它内部就会自己不停地发生变化不停地学习。
打比方说我们想要训练一个深度神经网络来识别猫。我们只需要不停地将猫的图片输入到神经网络中去。训练成功后,我们任意拿来一张新的图片,它都能判断出里面是否有猫。但我们并不知道他的分析过程是怎样的,它是如何判断里面是否有猫的。就像当我们教小孩子认识猫时,我们拿来一些白猫,告诉他这是猫,拿来一些黑猫,告诉他这也是猫,他脑子里会自己不停地学习猫的特征。最后我们拿来一些花猫,问他,他会告诉你这也是猫。但他是怎么知道的?他脑子里的分析过程是怎么样的?我们无从知道~~
如何输入数据
例如:如果要输入一张图像,计算机存储图像,要存储三个独立的矩阵,分别于红色、绿色和蓝色对应,矩阵里的数值就对应于图像的红绿蓝强度值。一般来说,为了方便处理,会将三个矩阵转换成一个向量x。
在人工智能领域,每一个输入到神经网络的数据都被叫做一个特征,这个用来表示的向量也被叫做特征向量。
神经网络接收这个特征向量x作为输入,并进行预测,然后给出相应的结果。
对于不同的应用,需要识别的对象不同,但是它们在计算机中都有对应的数字表示形式,通常我们会把它们转化成一个特征向量,然后将其输入到神经网络中。
如何预测
基本神经网络的预测基于一个简单的公式:z = dot(w, x) + b
x 代表输入的特征向量(如果有三个特征,那么x就可以用 (x1, x2, x3) 表示)
w 代表权重,它对应于每个输入特征,代表了每个特征的重要程度。
b 代表阈值,用来影响预测结果
z 就是预测结果
dot 表示将w和x进行向量相乘
激活函数
在神经网络中,我们不能直接用逻辑回归。必须要在逻辑回归外面再套上一个函数。这个函数称为激活函数。
最简单常用的一种叫做 sigmoid 的激活函数:
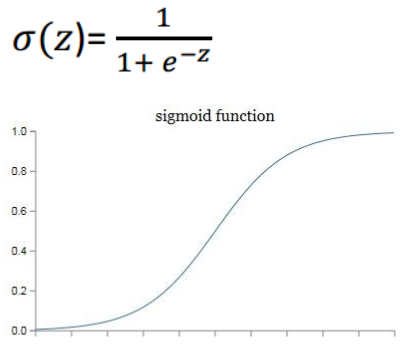
它的用途:把 z 映射到 [0,1] 之间,从而便于神经网络去进行计算
学习
神经网络是如何验证自己预测的结果是否准确呢?
只有知道自己预测的结果是否准确,才能够对自身进行调整,让结果越来越准确,这就是学习的过程。
验证学习成果,判断预测结果是否准确,一种方法就是 损失函数(loss function)
比如这个例子:我们使用预测结果与实际结果的差的平方乘以二分之一。
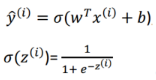

但是实际上我们使用的损失函数是: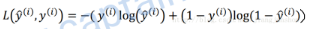
损失函数的计算结果越大,说明成本越大,即预测越不准确

梯度下降
预测结果是否准确是由 w 和 b 决定的,所以神经网络学习的目的就是要找到合适的 w 和 b。
通过一个叫做梯度下降的算法可以达到这个目的。梯度下降算法会一步步地改变w和b的值,新的w和b的值会使损失函数的输出结果更小,即一步步让预测更加准确。
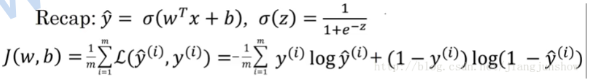
在上面提到的逻辑回归算法里,输入x和实际结果y都是固定的,损失函数其实是一个关于w和b的函数(w和b是变量)
学习 或者说 训练神经网络,其实就是找到一组 w和b ,使这个损失函数最小,即使结果更精准

损失函数 J 的形状是一个漏斗状。我们训练的目的就是找到在漏斗底部的一组 w和b
这种漏斗状的函数被称为 凸函数 ,选择 J 就是因为它是一个凸函数

如上图,梯度下降算法会一步步地更新 w和b,使损失函数一步步地变小,最终找到最小值或者接近最小值的地方
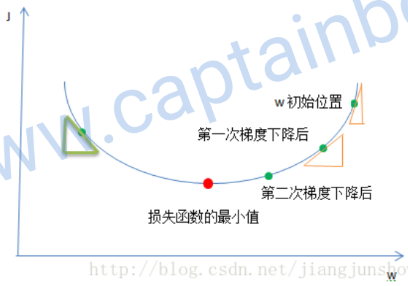
梯度下降更新参数的原理:
假设损失函数J只有一个参数w,并且假设w只是一个实数,则可以通过公式 w' = w - r * dw 来改变w的值。
梯度下降算法就是重复执行上面的公式来不停地更新w的值。新的w的值等于旧的w减去学习率r与偏导数dw的乘积。
r:学习步进、学习率(learning rate),r是我们用来控制w的变化步进的参数
dw:参数w关于损失函数J的偏导数
神经网络就是通过梯度下降算法来一步步改变w和b的值,使损失函数越来越小,使预测越来越精准