最长游程问题

关于这段的代码

 

     static void T12()
        {
            var dic = new String[] { "H", "T" };
            var total =1000000;
            var count=0;
            var k = 5;
            var n = 30;
            var rnd=new Random(Environment.TickCount);
            var parser = new PoissonParser();
            for (int i = 0; i < total; i++)
            {
                var sb = new StringBuilder();
                for (int index = 0; index < n; index++)
                {
                    sb.Append(dic[rnd.Next(2)]);
                }
                sb.Append("T");
                var str = sb.ToString();
                //Console.WriteLine(str);
                var info=parser.Do(str, i, k);
                count += info.Count;
                //Console.WriteLine(info);
                
            }
            Console.WriteLine("Total:{0},Count:{1},Rate:{2}", total, count,(double) count / (double)total);
        }

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace ConsoleApplication2
{
   public class Poisson
    {
      
    }
   public class ParserInfo
   {
       public int TrialId { get; set; }
       public List<int> Ei;
       public int n;
       public int Count
       {
           get
           {
               return Ei.Count;
              //下面对应这题目中实验出现k个连续正面的概率，注意多个Ei再一次实验中同事出现
              //也算1次出现
              // return Ei.Count>0? 1: 0; 
           }
       }
       public ParserInfo()
       {
           Ei = new List<int>();
       }
       public override string ToString()
       {
           var sb = new StringBuilder();
           sb.Append("TrialId:" + TrialId +"----");
           foreach (var i in Ei)
           {
               sb.Append("E" + i+",");
           }
          return sb.ToString().Trim(",".ToCharArray());
       }
   }
   public class PoissonParser
   {


       public PoissonParser()
       {
           
       }
       public ParserInfo Do(string serial, int trialId, int k)
       {
           var info = new ParserInfo();

           info.TrialId = trialId;
           info.n=serial.Length-1;     
           var queue=new Queue<int>();
           for (int i = 0; i < serial.Length; i++)
           {
               var c = serial[i];
               if (c == 'H')
               {
                   if (queue.Count == k)
                   {
                       queue.Dequeue();
                   }
                   queue.Enqueue(i);
                  
               }
               else if (c == 'T')
               {
                   if (queue.Count == k)
                   {
                       info.Ei.Add(queue.Dequeue()+1);
                   }
                   queue.Clear();
               }

               
           }
           return info;
       }
   }
}

题目只要求出现HH这样的字符序列那么这次实验（n个投掷算一个实验）就算出现了，至于HHHHT,HHHHT,HHTHH，都是并且记1次，

然后跟总的实验次数相除得到概率，比如记了x次，总的有y*n 那么就是x/y

所有题目的实际概率是求P(Ln>=k)出现的概率

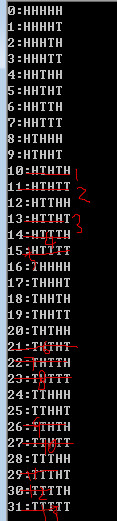
拿n=5,k=2来说，下面图片列出32种可能，而出现HH片段有19次，HHTHH我们统计时按一次来，所有E1 交 E4是不为空的。HHTHH出现

表示E1,E4同时发生了。

根据第9版p20也定义，无不相容事件，如果 EF=空 那么E与F互不相容 ，另外P(空）=0

明显当k,n选择适当参数时我们会发现Ei Ej 有不为空的情况

考虑k=2,n=5的情况，Ei定义参考课文

那么一次实验中HHTHH 的序列就是E1与E4同时出现了

clc
syms r
format long
n=5;
k=2;
p=1/2;
s=0;
for r=1: n-k+1
    c1=0;
    if n-r*k >= r
       c1=nchoosek((n-r*k),r);
    end
    c2=0;
    if(n-r*k >= r-1)
       c2=nchoosek(n-r*k,r-1); 
    end
    s=s + (-1)^(r+1) *( c1  +  (1/p)*c2 )  * p^(k*r)*(1-p)^r;
end

 

书上的实验指的是flips， 一次实验（n次投掷）的结果，由于Ei 嗯 Ej 可能同时出现，所有他们不是互不相容的

4b可以这样描述，E表示第一枚正面朝上，F表示第二枚正面操作， 现在求A有一枚正面朝上的概率。这样描述就跟上面的游程

一样。即P(A)=P(E 并 F)。 并且一次实验中E,F可能同时出现。

有4种情况 HH,HT,TH,TT,   P(A)=3/4,  P(E)=1/2  P(F)=1/2  ,  P(EF)=1/4 ,按公式（2.4节命题4.4)  ,1/2 +1/2 -1/4=3/4;