机器学习知识体系

这是机器学习知识体系中的逻辑回归内容，完整的知识体系可以查看这里。

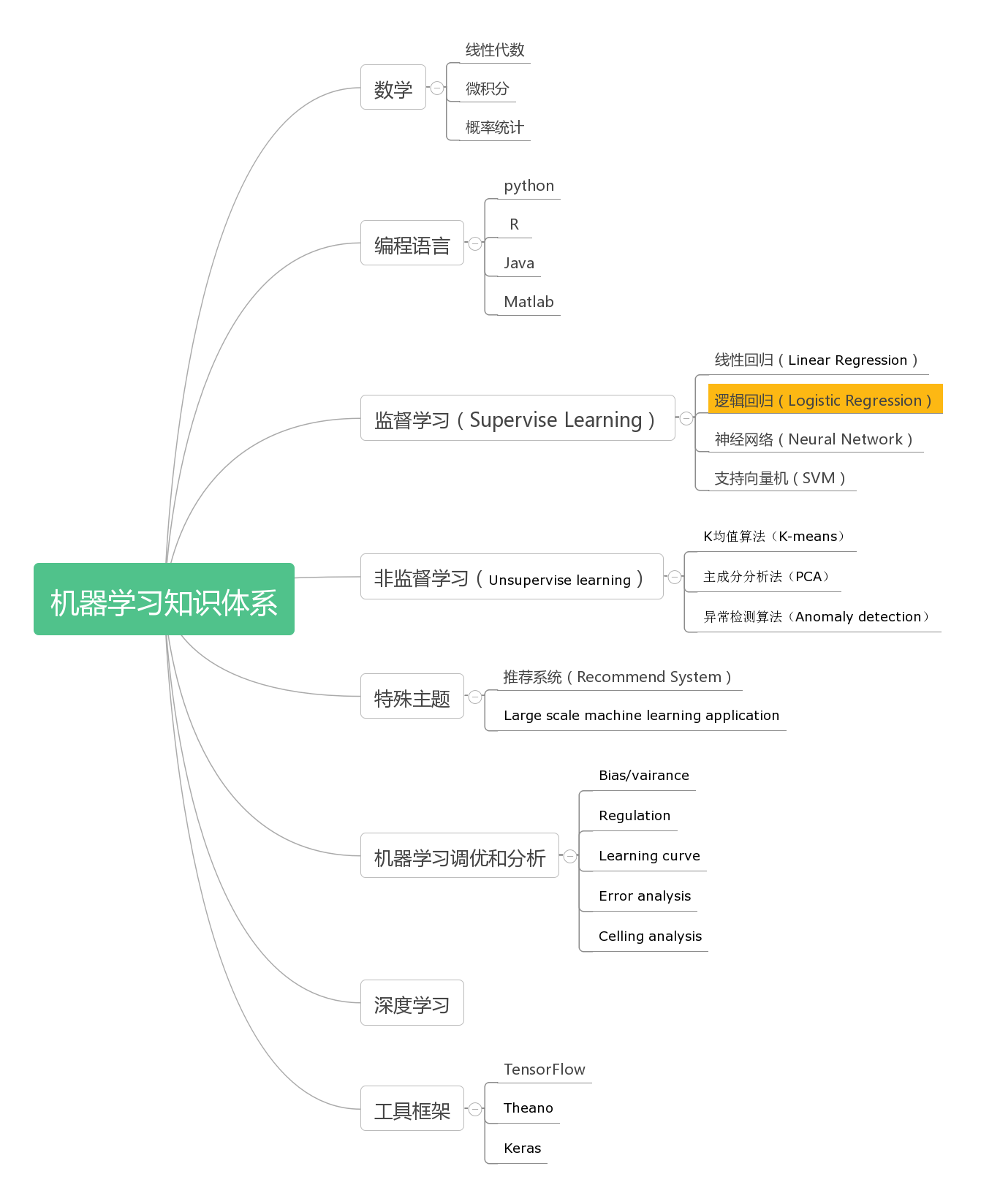
分类问题和逻辑回归

不同于线性回归，逻辑回归是用于解决离散型的输出结果的问题（分类问题）。典型的分类问题例如：

- 判断是否垃圾邮件

- 判断肿瘤良恶性

- 判断是否存在恶意的在线交易 

对于分类问题，y的输出等于 0 或者 1。逻辑回归函数式输出，它的输出范围是: 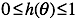，以0.5作为临界值（Threshhold），y的取值如下：

如果 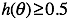，y = 1

如果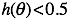， y = 0

函数式表达

逻辑回归的函数表达如下：

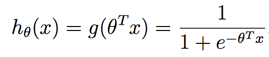
其中

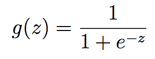
被称为logistic function 或者 sigmoid function。这个函数图形如下：

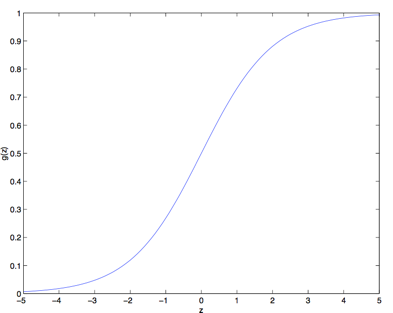
在这里我们不去研究如何得出这个函数，但可以仔细观察这个函数的几点特性：

1. g(z)是一个输出值在[0,1]的函数，并且当z >= 0, g(z) >= 0.5，z < 0, g(z) < 0.5，所以从这点来说非常符合我们对逻辑回归函数的期望。

2. 这个函数在z=0附近曲率非常陡峭，所以输出值很有很大的区分度。举个例子，一旦z > 0，那么g(z)往往会比0.5大较多。

代价函数

逻辑回归的代价函数如下：

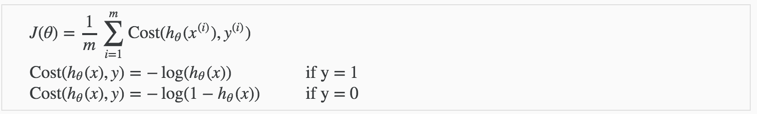
代价函数的图形如下：

  

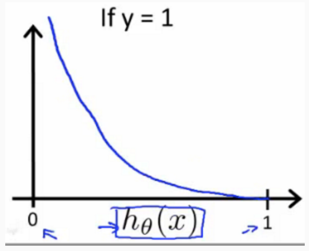
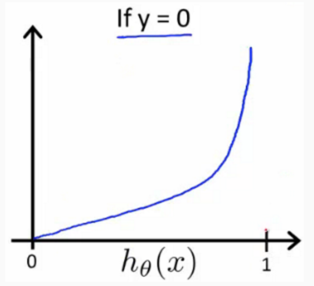
可以看出:

当y=1时： h(x) -> 1, cost(h(x), y) -> 0， h(x) -> 0, cost(h(x),y) ->  

当y=0时： h(x) -> 0, cost(h(x), y) -> 0， h(x) -> 1, cost(h(x),y) ->  

所以这个函数很好的表达了我们的意愿，h(x)和y越是接近，代价函数越小，反之则越大，并且这个函数是个凹函数始终存在最优解。

将y=1和y=0的代价函数合并，可以得到如下函数

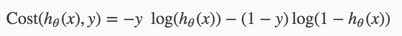
整个代价函数表示如下：

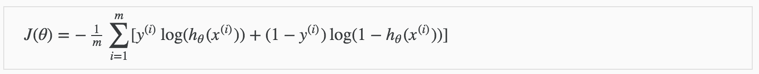
梯度下降算法

梯度下降算法基本方式如下：

所以关键是推导出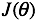对于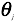的偏导数如下：

"Conjugate gradient", "BFGS", 和 "L-BFGS" 算法可以比梯度下降算法更好的计算出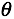，所以建议可以直接使用Octave或者matlab里面自带的方法。

1. 首先需要计算出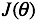 和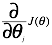

function [jVal, gradient] = costFunction(theta)
jVal = [...code to compute J(theta)...];
gradient = [...code to compute derivative of J(theta)...];
end

2. 使用“fminunc()”方法计算出

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

 

多分类问题

多分类问题指的是分类存在多种情况：

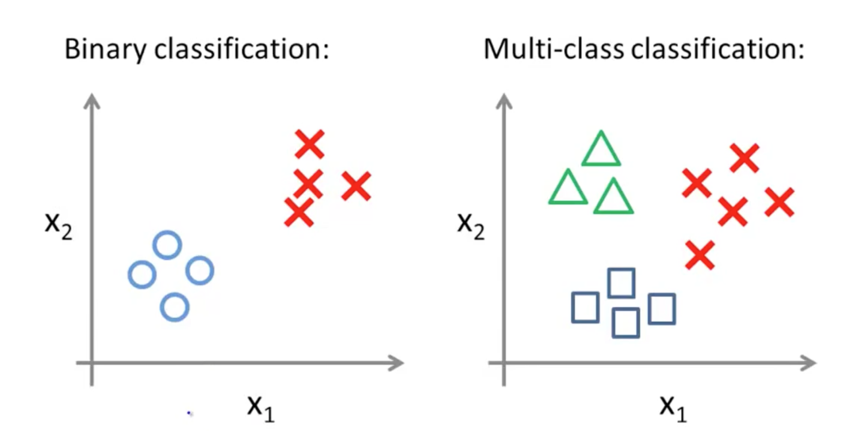
对于多分类问题，我们通常将其转化成Binary Classification问题，例如：

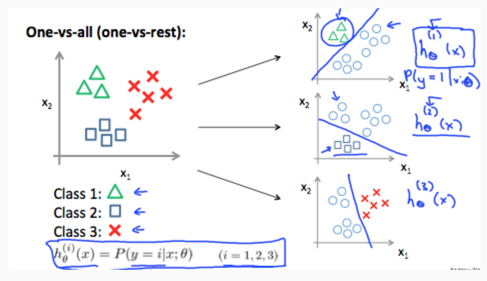
我们把Class 1（三角形）标记为一种类型，然后把其他几种类型都当成另一种类型，然后训练出 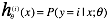，h(x) 代表 y = i的概率情况。于是每个分类，我们都可以得出对应的h(x)。

所以将来对于一个测试数据x，我们需要找到那个 i （某个分类）可以最大化 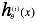, 于是那个 i 就是测试数据x对应的分类值。