回归_最小二乘法（python脚本实现）

zoukankan html css js c++ java

回归_最小二乘法（python脚本实现）
python机器学习-乳腺癌细胞挖掘（博主亲自录制视频）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

机器学习，统计项目联系：QQ：231469242
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pylab as plt from scipy import stats x = [3.5, 2.5, 4.0, 3.8, 2.8, 1.9, 3.2, 3.7, 2.7, 3.3] #高中平均成绩 y = [3.3, 2.2, 3.5, 2.7, 3.5, 2.0, 3.1, 3.4, 1.9, 3.7] #大学平均成绩 #linregress(x,y)线性回归函数 slope, intercept, r_value, p_value, std_err = stats.linregress(x,y) ''' Out[37]: LinregressResult(slope=0.70389344262295073, intercept=0.71977459016393475, rvalue=0.68345387256609358, pvalue=0.029341978126562161, stderr=0.26581031503816904) ''' slope = round(slope,3) intercept = round(intercept,3) print slope, intercept #绘图用 def f(x, a, b): return a + b*x xdata = np.linspace(1, 5, 20) plt.grid(True) plt.xlabel('x axis') plt.ylabel('y axis') plt.text(2.5, 4.0, r'$y = ' + str(intercept) + ' + ' + str(slope) +'*x$', fontsize=18) plt.plot(xdata, f(xdata, intercept,slope), 'b', linewidth=1) plt.plot(x,y,'ro') plt.show()
作者Toby qq:231469242
http://www.cnblogs.com/NanShan2016/p/5493429.html

最小二乘法本身实现起来也是不难的，就如我们上面所说的不断调整参数，然后令误差函数Err不断减小就行了。

With the advent of cheap computing power, statistical modeling has been a booming
field. This has also affected classical statistical analysis, as most problems can be
viewed from two perspectives: one can either make a statistical hypothesis, and
verify or falsify that hypothesis; or one can make a statistical model, and analyze
the significance of the model parameters.
Let me use a classical t-test as an example.

StatisticalModeling
Expressed as a statistical model, we assume that the difference between the first
and the second race is simply a constant value. (The null hypothesis would be that
this value is equal to zero.) This model has one parameter: the constant value. We
can find this parameter, as well as its confidence interval and a lot of additional
information, with the following Python code
# -*- coding: utf-8 -*- ''' The command random.seed(123) initializes the random number generator with the number 123, which ensures that two consecutive runs of this code produce the same result, corresponding to the numbers given above. ''' import numpy as np from scipy import stats # Generate the data np.random.seed(123) race_1 = np.round(np.random.randn(20)*10+90) race_2 = np.round(np.random.randn(20)*10+85) # t-test (t, pVal) = stats.ttest_rel (race_1, race_2) # Show the result print('The probability that the two distributions ' 'are equal is {0:5.3f} .'.format(pVal)) import pandas as pd import statsmodels.formula.api as sm np.random.seed(123) df = pd.DataFrame({'Race1': race_1, 'Race2':race_2}) result = sm.ols(formula='I(Race2-Race1) ~ 1', data=df).fit() print(result.summary())
statsmodels是一个包含统计模型、统计测试和统计数据挖掘python模块。对每一个模型都会生成一个对应的统计结果。统计结果会和现有的统计包进行对比来保证其正确性。

1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。

高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中。

法国科学家勒让德于1806年独立发明“最小二乘法”，但因不为世人所知而默默无闻。

二乘法(2张)

勒让德曾与高斯为谁最早创立最小二乘法原理发生争执。

1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明，因此被称为高斯-马尔可夫定理。（来自于wikipedia）
参考：https://www.zhihu.com/question/37031188/answer/111336809

最小二乘法(Least Squares Method,简记为LSE)是一个比较古老的方法，源于天文学和测地学上的应用需要。在早期数理统计方法的发展中，这两门科学起了很大的作用。丹麦统计学家霍尔把它们称为“数理统计学的母亲”。此后近三百年来，它广泛应用于科学实验与工程技术中。美国统计史学家斯蒂格勒( S. M. Stigler)指出, 最小二乘方法是19世纪数理统计学的压倒一切的主题。1815年时,这方法已成为法国、意大利和普鲁士在天文和测地学中的标准工具,到1825年时已在英国普遍使用。

追溯到1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯根据高斯计算出来的轨道重新发现了谷神星。高斯于其1809年的著作《关于绕日行星运动的理论》中。在此书中声称他自1799年以来就使用最小二乘方法,由此爆发了一场与勒让德的优先权之争。

近代学者经过对原始文献的研究,认为两人可能是独立发明了这个方法,但首先见于书面形式的，以勒让德为早。然而,现今教科书和著作中,多把这个发明权归功于高斯。其原因,除了高斯有更大的名气外,主要可能是因为其正态误差理论对这个方法的重要意义。勒让德在其著作中,对最小二乘方法的优点有所阐述。然而,缺少误差分析。我们不知道,使用这个方法引起的误差如何,就需建立一种误差分析理论。高斯于1823年在误差e1 ,… , en独立同分布的假定下,证明了最小二乘方法的一个最优性质: 在所有无偏的线性估计类中,最小二乘方法是其中方差最小的！在德国10马克的钞票上有高斯像，并配了一条正态曲线。在高斯众多伟大的数学成就中挑选了这一条,亦可见这一成就对世界文明的影响。

现行的最小二乘法是勒让德( A. M. Legendre)于1805年在其著作《计算慧星轨道的新方法》中提出的。它的主要思想就是选择未知参数，使得理论值与观测值之差的平方和达到最小：
$H=sum_{0}^{m}{(y-y_{i})}$

我们现在看来会觉得这个方法似乎平淡无奇,甚至是理所当然的。这正说明了创造性思维之可贵和不易。从一些数学大家未能在这个问题上有所突破,可以看出当时这个问题之困难。欧拉、拉普拉斯在许多很困难的数学问题上有伟大的建树,但在这个问题上未能成功。

在高斯发表其1809年著作之前，约在1780年左右,拉普拉斯已发现了概率论中的“中心极限定理”。根据这个定理，大量独立的随机变量之和,若每个变量在和中起的作用都比较小，则和的分布必接近于正态。测量误差正具有这种性质。一般地说,随机(而非系统)的测量误差，是出自大量不显著的来源的叠加。因此，中心极限定理给误差的正态性提供了一种合理的理论解释。这一点对高斯理论的圆满化很有意义,因为高斯原来的假定(平均数天然合理)总难免给人一种不自然的感觉。

耐人寻味的是,无论是中心极限定理的发明者拉普拉斯,还是早就了解这一结果的高斯,都没有从这个结果的启示中去考察误差分布问题。对前者而言,可能是出于思维定势的束缚,这对拉普拉斯来说可算不幸,他因此失掉了把这个重要分布冠以自己名字的机会(正态分布这个形式最早是狄莫弗( De Moiv re) 1730年在研究二项概率的近似计算时得出的。以后也有其他学者使用过,但都没有被冠以他们的名字。高斯之所以获得这一殊荣,无疑是因为他把正态分布与误差理论联系了起来) 。

可以说,没有高斯的正态误差理论配合, 最小二乘方法的意义和重要性可能还不到其现今所具有的十分之一。最小二乘方法方法与高斯误差理论的结合,是数理统计史上最重大的成就之一,其影响直到今日也尚未过时！由于本文是主要介绍最小二乘法与矩阵投影之间的关系，对于最小二乘和概率之间的关系，请参看靳志辉的《正态分布的前世今生》。

那么，投影矩阵与最小二乘二者有什么必然的联系么，当我开始写这篇文章的时候我也这样问自己。先说说投影吧，这个想必大家都知道，高中的知识了。一个向量在另一个向量上的投影，实际上就是寻找在上离最近的点。

现在我们假设投影点是向量上的一点p，可以规定p=xa（x是某个数）。定义e=b-p，称e 为误差。因为e 与p 也就是a 垂直，所以有 $a^{T}(b-ax)=0$ ，展开化简得到：

$x=frac{a^{T}}{a^{T}a} cdot b$ ， $p=ax=frac{aa^{T}}{a^{T}a} cdot b$

我们发现：如果改变b，那么p相对应改变，然而改变a，p无变化。接下来，我们可以考虑更高维度的投影，三维空间的投影是怎么样的呢，我们可以想象一个三维空间内的向量在该空间内的一个平面上的投影：

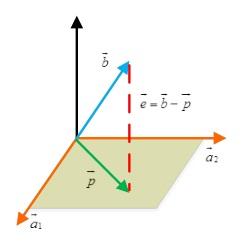
我们假设这个平面的基(basis)是a1, a2。那么矩阵A 的列空间就是该平面。假设一个不在该平面上的向量b 在该平面上的投影是p 。我们的任务就是找到合适的x，使得p=Ax 。这里有一个关键的地方：e 与该平面垂直，所以 $A^{T}(b-Ax)=0$ 。我们把上边式子展开，得到

$x=(A^{T}A)^{-1}A^{T}cdot b$ , $p=Ax=A(A^{T}A)^{-1}A^{T}cdot b$

有了上面的背景知识，我们可以正式进入主题了，投影矩阵(projection matrix)：
$P=A(A^{T}A)^{-1}A^{T}$

这里我们最需要关注的是投影矩阵的两个性质：

1） $P^{T}= P$ ;

2） $P^{2}= P$ ;

对于第一个，很容易理解，因为P本身就是个对称阵。第二个，直观的理解就是投影到a上后再投影一次，显然投影并没有改变，也就是二次投影还是其本身。

这个投影到底有什么用呢？从上面的分析中我们可以看出：投影矩阵P可以吧向量b投影成向量p！从线性代数的角度来说，Ax=b并不一定总有解，这在实际情况中会经常遇到（m > n）。所以我们就把b投影到向量p上，因为p在a1，a2的平面内，所以Ax =p是可以求解的。

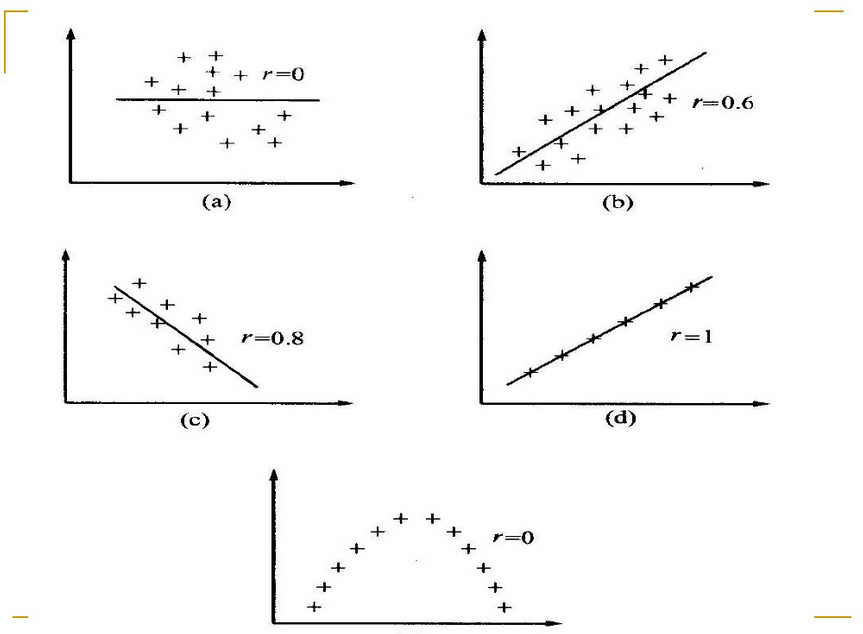
好了，在此我们先暂别“投影”。下面，开始说一下最小二乘的故事吧：在实际应用中，线性回归是经常用到的，我们可以在一张散列点图中作一条直线（暂时用直线）来近似表述这些散列点的关系。比如：

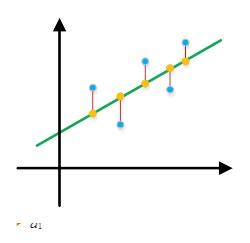
设变量y 与t 成线性关系,即.现在已知m 个实验点ai和bi ,求两个未知参数C,D 。将代入得矛盾方程组

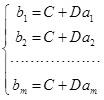
令

,

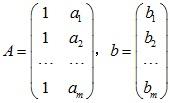则可写成Ax=b形式。从线性代数的角度来看，就是A的列向量的线性组合无法充满整个列空间，也就是说Ax=b这个方程根本没有解。从图形上也很好理解：根本没有一条直线同时经过所有蓝色的点！所以为了选取最合适的x，让该等式"尽量成立"，引入残差平方和函数H：
$min(H)=min(||e||^{2})=min(||b-Ax||^{2})$

这也就是最小二乘法的思想。我们知道，当x取最优值的时候，Ax恰好对应图中线上橙色的点，而b则对应图中蓝色的点，e的值则应红色的线长。

看到这里你有没有和之前投影的那部分知识联系在一起呢？最小二乘的思想是想如何选取参数x使得H最小。而从向量投影的角度来看这个问题，H就是向量e长度的平方，如何才能使e的长度最小呢？b和a1，a2都是固定的，当然是e垂直a1，a2平面的时候长度最小！换句话说：最小二乘法的解与矩阵投影时对变量求解的目标是一致的！

为了定量地给出与实验数据之间线性关系的符合程度,可以用相关系数来衡量.它定义为

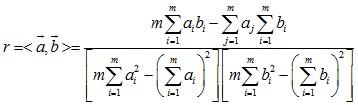
r也就是我们之前介绍的向量夹角。r 值越接近1, y与t 的线性关系越好.为正时,直线斜率为正,称为正相关；r 为负时,直线斜率为负,称为负相关.接近于0时,测量数据点分散或之间为非线性.不论测量数据好坏都能求出和,所以我们必须有一种判断测量数据好坏的方法,用来判断什么样的测量数据不宜拟合,判断的方法是时,测量数据是非线性的. r0称为相关系数的起码值,与测量次数n 有关。

最小二乘讲到这里似乎已经说完了，但是有一个问题，那就是我们所利用的投影矩阵P这里我们假定 $A^{T}A$ 是可逆的，这种假定合理吗？Strang在最后给我们作了解答：

If A has independent columns, then A'A is invertible

写到这里，我想有必要总结一下，为什么最小二乘和投影矩阵要扯到一起，它们有什么联系：最小二乘是用于数据拟合的一个很霸气的方法，这个拟合的过程我们称之为线性回归。如果数据点不存在离群点（outliers），那么该方法总是会显示其简单粗暴的一面。我们可以把最小二乘的过程用矩阵的形式描述出来，然而，精妙之处就在于，这与我们的投影矩阵的故事不谋而合，所以，我们又可以借助于投影矩阵的公式，也就是 $A^{T}Ax = A^{T}b$ 来加以解决。

最小二乘法是从误差拟合角度对回归模型进行参数估计或系统辨识,并在参数估计、系统辨识以及预测、预报等众多领域中得到极为广泛的应用。在数据拟合领域，最小二乘法及其各种变形的拟合方法包括:一元线性最小二乘法拟合、多元线性拟合、多项式拟合、非线性拟合。最小二乘法能将从实验中得出的一大堆看上去杂乱无章的数据中找出一定规律,拟合成一条曲线来反映所给数据点总趋势,以消除其局部波动。它为科研工作者提供了一种非常方便实效的数据处理方法。随着现代电子计算机的普及与发展，这个占老的方法更加显示出其强大的生命力。

想了解更多有关矩阵的内容，可以搜索《神奇的矩阵》。

http://www.cnblogs.com/NanShan2016/p/5493429.html参考

自从开始做毕设以来，发现自己无时无刻不在接触最小二乘法。从求解线性透视图中的消失点，m元n次函数的拟合，包括后来学到的神经网络，其思想归根结底全都是最小二乘法。

1-1 “多线→一点”视角与“多点→一线”视角

最小二乘法非常简单，我把它分成两种视角描述：

（1）已知多条近似交汇于同一个点的直线，想求解出一个近似交点：寻找到一个距离所有直线距离平方和最小的点，该点即最小二乘解；

（2）已知多个近似分布于同一直线上的点，想拟合出一个直线方程：设该直线方程为y=kx+b，调整参数k和b，使得所有点到该直线的距离平方之和最小，设此时满足要求的k=k0，b=b0，则直线方程为y=k0x+b0。

1-2 思维拓展

这只是举了两个简单的例子，其实在现实生活中我们可以利用最小二乘法解决更为复杂的问题。比方说有一个未知系数的二元二次函数f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5，这里w0~w5为未知的参数，为了确定下来这些参数，将会给定一些样本点(xi,yi,f(xi,yi))，然后通过调整这些参数，找到这样一组w0~w5，使得这些所有的样本点距离函数 f(x,y)的距离平方之和最小。至于具体用何种方法来调整这些参数呢？有一种非常普遍的方法叫“梯度下降法”，它可以保证每一步调整参数，都使得 f(x,y)朝比当前值更小的方向走，只要步长α选取合适，我们就可以达成这种目的。

而这里不得不提的就是神经网络了。神经网络其实就是不断调整权值w和偏置b，来使得cost函数最小，从这个意义上来讲它还是属于最小二乘法。更为可爱的一点是，神经网络的调参用到的仍是梯度下降法，其中最常用的当属随机梯度下降法。而后面伟大的bp算法，其实就是为了给梯度下降法做个铺垫而已，bp算法的结果是cost函数对全部权值和全部偏置的偏导，而得知了这些偏导，对于各个权值w和偏置b该走向何方就指明了方向。

因此，最小二乘法在某种程度上无异于机器学习中基础中的基础，且具有相当重要的地位。至于上面所说的“梯度下降法”以及“利用最小二乘法求解二元二次函数的w0~w5”，我将会在后面的博客中进行更加详细的探讨。

2 scipy库中的leastsq函数

当然，最小二乘法本身实现起来也是不难的，就如我们上面所说的不断调整参数，然后令误差函数Err不断减小就行了。我们将在下一次博客中详细说明如何利用梯度下降法来完成这个目标。

而在本篇博客中，我们介绍一个scipy 库中的函数，叫leastsq，它可以省去中间那些具体的求解步骤，只需要输入一系列样本点，给出待求函数的基本形状（如我刚才所说，二元二次函数就是一种形状——f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5，在形状给定后，我们只需要求解相应的系数w0~w6），即可得到相应的参数。至于中间到底是怎么求的，这一部分内容就像一个黑箱一样。

2-1 函数形为y=kx+b

这一次我们给出函数形y=kx+b。这种情况下，待确定的参数只有两个：k和b。

此时给出7个样本点如下：

1 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 2 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])

则使用leastsq函数求解其拟合直线的代码如下：

1 ###最小二乘法试验### 2 import numpy as np 3 from scipy.optimize import leastsq 4 5 ###采样点(Xi,Yi)### 6 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 7 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05]) 8 9 ###需要拟合的函数func及误差error### 10 def func(p,x): 11 k,b=p 12 return k*x+b 13 14 def error(p,x,y,s): 15 print s 16 return func(p,x)-y #x、y都是列表，故返回值也是个列表 17 18 #TEST 19 p0=[100,2] 20 #print( error(p0,Xi,Yi) ) 21 22 ###主函数从此开始### 23 s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的k、b 24 Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中 25 k,b=Para[0] 26 print"k=",k,' ',"b=",b 27 28 ###绘图，看拟合效果### 29 import matplotlib.pyplot as plt 30 31 plt.figure(figsize=(8,6)) 32 plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点 33 x=np.linspace(0,10,1000) 34 y=k*x+b 35 plt.plot(x,y,color="orange",label="Fitting Line",linewidth=2) #画拟合直线 36 plt.legend() 37 plt.show()

我把里面需要注意的点提点如下：

1、p0里放的是k、b的初始值，这个值可以随意指定。往后随着迭代次数增加，k、b将会不断变化，使得error函数的值越来越小。

2、func函数里指出了待拟合函数的函数形状。

3、error函数为误差函数，我们的目标就是不断调整k和b使得error不断减小。这里的error函数和神经网络中常说的cost函数实际上是一回事，只不过这里更简单些而已。

4、必须注意一点，传入leastsq函数的参数可以有多个，但必须把参数的初始值p0和其它参数分开放。其它参数应打包到args中。

5、leastsq的返回值是一个tuple，它里面有两个元素，第一个元素是k、b的求解结果，第二个元素我暂时也不知道是什么意思，先留下来。

其拟合效果图如下：

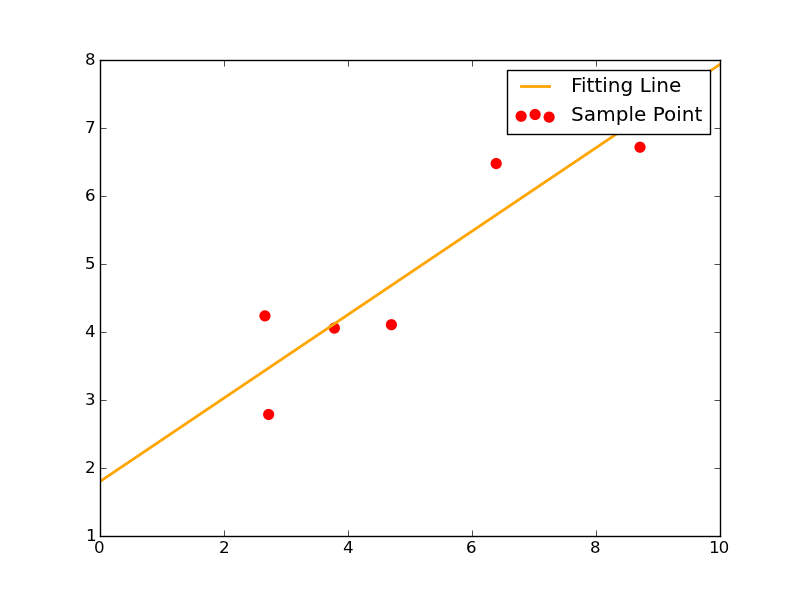
2-2 函数形为y=ax^2+bx+c

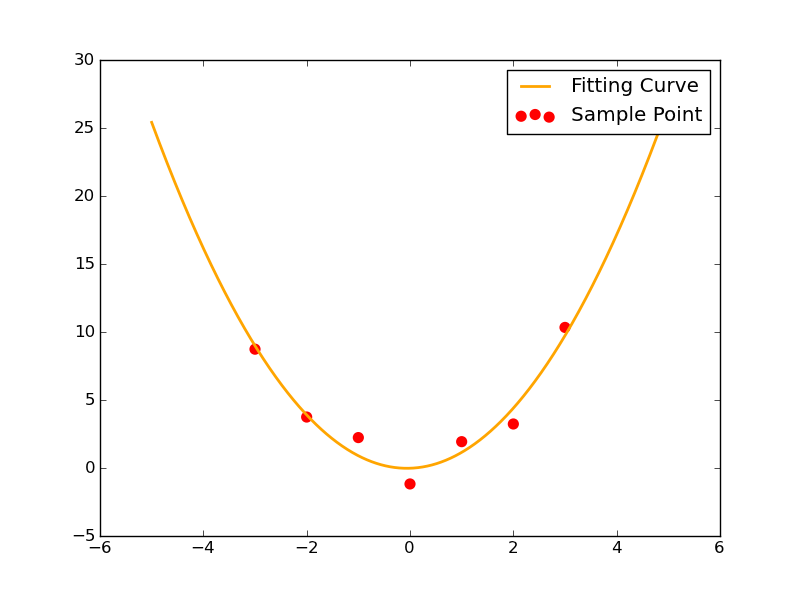
这一次我们给出函数形y=ax^2+bx+c。这种情况下，待确定的参数有3个：a，b和c。

此时给出7个样本点如下：

1 Xi=np.array([0,1,2,3,-1,-2,-3]) 2 Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7])

这一次的代码与2-1差不多，除了把待求参数再增加一个，换了一下训练样本，换了一下func中给出的函数形，几乎没有任何变化。

1 ###最小二乘法试验### 2 import numpy as np 3 from scipy.optimize import leastsq 4 5 ###采样点(Xi,Yi)### 6 Xi=np.array([0,1,2,3,-1,-2,-3]) 7 Yi=np.array([-1.21,1.9,3.2,10.3,2.2,3.71,8.7]) 8 9 ###需要拟合的函数func及误差error### 10 def func(p,x): 11 a,b,c=p 12 return a*x**2+b*x+c 13 14 def error(p,x,y,s): 15 print s 16 return func(p,x)-y #x、y都是列表，故返回值也是个列表 17 18 #TEST 19 p0=[5,2,10] 20 #print( error(p0,Xi,Yi) ) 21 22 ###主函数从此开始### 23 s="Test the number of iteration" #试验最小二乘法函数leastsq得调用几次error函数才能找到使得均方误差之和最小的a~c 24 Para=leastsq(error,p0,args=(Xi,Yi,s)) #把error函数中除了p以外的参数打包到args中 25 a,b,c=Para[0] 26 print"a=",a,' ',"b=",b,"c=",c 27 28 ###绘图，看拟合效果### 29 import matplotlib.pyplot as plt 30 31 plt.figure(figsize=(8,6)) 32 plt.scatter(Xi,Yi,color="red",label="Sample Point",linewidth=3) #画样本点 33 x=np.linspace(-5,5,1000) 34 y=a*x**2+b*x+c 35 plt.plot(x,y,color="orange",label="Fitting Curve",linewidth=2) #画拟合曲线 36 plt.legend() 37 plt.show()

不过我们发现，它依旧能够非常顺利地解出待求的三个参数。其拟合情况如图所示：

2-3 leastsq拟合y=kx+b可视化

本部分内容是建立在2-1代码的基础上，用Mayavi绘3D图，以简单地说明最小二乘法到底是怎么一回事。该部分知识用到了mgrid函数，具体是如何实施的请移步《Python闲谈（一）mgrid慢放》。

step 1：创建一个k矩阵和b矩阵。在mgrid扩展后，有：

（1）k=[k1,k2,k3,...,kn]

mgrid(k)（朝右扩展）= [k1,k1,k1,...,k1] [k2,k2,k2,...,k2] [k3,k3,k3,...,k3] ... [kn,kn,kn,...,kn]

（2）b=[b1,b2,b3,...,bn]

mgrid(b)（朝下扩展）= [b1,b2,b3,...,bn] [b1,b2,b3,...,bn] [b1,b2,b3,...,bn] ... [b1,b2,b3,...,bn]

其中k矩阵和b矩阵等大（皆为n维向量,或者说1*n的矩阵），且这两个矩阵里面的元素都非常密集。举个例子以说明什么叫矩阵中的元素很密集：a是个矩阵，假设a_ij 为a矩阵中第i行第j列元素，则a_ij 和 a_{i+1}j 的差值很小，a_ij 和 a_i{j+1} 的差值也很小。也就是同一行或者同一列中相邻的两个元素的值非常接近。为什么要让矩阵元素如此密集呢？因为我们的根本目的是用“密集的离散”来逼近“连续”，这里的思想就像微积分一样。

而放在这里，就是ku和k{u+1}很接近，bv和b{v+1}也很接近。

step 2：令k矩阵和b矩阵中的元素按照其位置一一对应。对应后的结果为：

Combine_kb= [(k1,b1),(k1,b2),(k1,b3)...,(k1,bn)] [(k2,b1),(k2,b2),(k2,b3)...,(k2,bn)] [(k3,b1),(k3,b2),(k3,b3)...,(k3,bn)] ... [(kn,b1),(kn,b2),(kn,b3)...,(kn,bn)]

step 3：对矩阵中每一个(ku,bv)，我们分别求出该种情况下每一个训练样本点的误差平方之和，即有：

Err{(ku,bv)}=∑{i=1~m}（(yi-（ku*xi+bv）)**2）

其中m为给定的训练样本点的个数。例如在这里：

1 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 2 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])

则有m=7。

什么意思呢？举个例子，当i=1的时候，这个时候把(x1,y1)（= （8.19,7.01））代入（(yi-（ku*xi+bv）)**2）式子里面，由于此时已经锁定(ku,bv)，因此式中所有的数都是常数，我们可以解出一个常数（(y1-（ku*x1+bv）)**2）。然后依次令i=2,3,4,...,7,可以分别求解出一个（(yi- （ku*xi+bv）)**2）值来，这7个（(yi-（ku*xi+bv）)**2）值加起来即Err{(ku,bv)}。

注意了，最终我们算出的那个Err{(ku,bv)}将会存放到ku、bv对应的那个位置，比方说u=3,v=2：

mgrid(k)=

[k1,k1,k1,...,k1]

[k2,k2,k2,...,k2]

[k3,k3,k3,...,k3]

...

[kn,kn,kn,...,kn]

mgrid(b)=

[b1,b2,b3,...,bn]

[b1,b2,b3,...,bn]

[b1,b2,b3,...,bn]

...

[b1,b2,b3,...,bn]

则刚才算出来的Err{(k3,b2)}应该放在这个位置：

Err=

[Err11,Err12,Err13,...,Err1n]

[Err21,Err22,Err23,...,Err2n]

[Err31,Err32,Err33,...,Err3n]

...

[Errn1,Errn2,Errn3,...,Errnn]

如此这般对于每一对(ku,bv)都这样算，则上方的Err矩阵中每一个元素的值都可以算出来；将计算出的结果正确地放在Err矩阵中对应位置，即得到Err矩阵。

step 4：绘制曲面。

截至目前我们已经得到了两个重要矩阵Combine_kb和Err，其中Combine_kb提供点的x、y轴坐标，Err矩阵提供点的z轴坐标。

Combine_kb= [(k1,b1),(k1,b2),(k1,b3)...,(k1,bn)] [(k2,b1),(k2,b2),(k2,b3)...,(k2,bn)] [(k3,b1),(k3,b2),(k3,b3)...,(k3,bn)] ... [(kn,b1),(kn,b2),(kn,b3)...,(kn,bn)]

Err= [Err11,Err12,Err13,...,Err1n] [Err21,Err22,Err23,...,Err2n] [Err31,Err32,Err33,...,Err3n] ... [Errn1,Errn2,Errn3,...,Errnn]

我们再将这两个矩阵合并一下得到Combine_kbErr矩阵：

Combine_kbErr= [(k1,b1,Err11),(k1,b2,Err12),(k1,b3,Err13)...,(k1,bn,Err1n)] [(k2,b1,Err21),(k2,b2,Err22),(k2,b3,Err23)...,(k2,bn,Err2n)] [(k3,b1,Err31),(k3,b2,Err32),(k3,b3,Err33)...,(k3,bn,Err3n)] ... [(kn,b1,Errn1),(kn,b2,Errn2),(kn,b3,Errn3)...,(kn,bn,Errnn)]

在三维空间直角坐标系下绘制出Combine_kbErr中的每一个点，然后将这些点与其各自相邻的点连起来，则得到我们想要的Err(k,b)函数曲面。

step 5：本部分代码如下：

1 """part 2""" 2 ###定义一个函数，用于计算在k、b已知时∑((yi-(k*xi+b))**2)### 3 def S(k,b): 4 ErrorArray=np.zeros(k.shape) #k的shape事实上同时也是b的shape 5 for x,y in zip(Xi,Yi): #zip(Xi,Yi)=[(8.19,7.01),(2.72,2.78),...,(3.78,4.05)] 6 ErrorArray+=(y-(k*x+b))**2 7 return ErrorArray 8 9 ###绘制ErrorArray+最低点### 10 from enthought.mayavi import mlab 11 12 #画整个Error曲面 13 k,b=np.mgrid[k0-1:k0+1:10j,b0-1:b0+1:10j] 14 Err=S(k,b) 15 face=mlab.surf(k,b,Err/500.0,warp_scale=1) 16 mlab.axes(xlabel='k',ylabel='b',zlabel='Error') 17 mlab.outline(face) 18 19 #画最低点（即k，b所在处） 20 MinErr=S(k0,b0) 21 mlab.points3d(k0,b0,MinErr/500.0,scale_factor=0.1,color=(0.5,0.5,0.5)) #scale_factor用来指定点的大小 22 mlab.show()

对要点说明如下：

1、为了让最小二乘法求解的结果出现在绘制曲面的范围内，我们以最终leastsq求得的k0、b0为中心创建k向量和b向量。

2、传入S函数的是k向量和b向量mgrid后的结果。

3、S函数中的ErrorArray+=(y-(k*x+b))**2 操作里，k、b皆为矩阵（是k、b向量mgrid后的结果），而x、y皆为常数，故这里的操作实际上是对矩阵的操作。这个ErrorArray就是上面我说的Err矩阵。

4、在绘图时之所以对Err除以500，是因为Err和k、b的差距不是一般的大，直接绘图会导致什么都看不出来。举一个最简单的例子就是比如我们要画个二维直角坐标系下的图，x的取值范围是0~1，y的取值范围是0~1000，而两个坐标轴却都按一个单位△x=△y=0.1来画，想想看结果会成什么样子？

这里也是同样的道理，于是得给Err除以一个大数才能让图像正常显示。

其实matplotlib画三维坐标系下的图会帮你调整到合适，只有Mayavi才会出现这种情况，反正注意一下比例问题就好了。

5、该程序除过绘制Err曲面外，还把(k0,b0)也画出来了，见灰色小球。

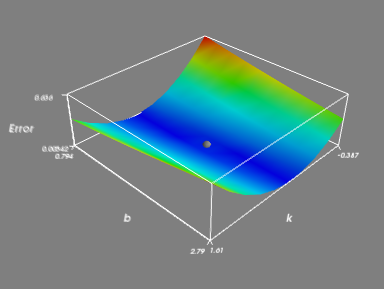
step 6：整个程序的全部代码如下，其中part1与2-1的代码是完全一样的。

1 ###【最小二乘法试验】### 2 import numpy as np 3 from scipy.optimize import leastsq 4 5 ###采样点(Xi,Yi)### 6 Xi=np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78]) 7 Yi=np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05]) 8 9 """part 1""" 10 ###需要拟合的函数func及误差error### 11 def func(p,x): 12 k,b=p 13 return k*x+b 14 15 def error(p,x,y): 16 return func(p,x)-y #x、y都是列表，故返回值也是个列表 17 18 p0=[1,2] 19 20 ###最小二乘法求k0、b0### 21 Para=leastsq(error,p0,args=(Xi,Yi)) #把error函数中除了p以外的参数打包到args中 22 k0,b0=Para[0] 23 print"k0=",k0,' ',"b0=",b0 24 25 """part 2""" 26 ###定义一个函数，用于计算在k、b已知时，∑((yi-(k*xi+b))**2)### 27 def S(k,b): 28 ErrorArray=np.zeros(k.shape) #k的shape事实上同时也是b的shape 29 for x,y in zip(Xi,Yi): #zip(Xi,Yi)=[(8.19,7.01),(2.72,2.78),...,(3.78,4.05)] 30 ErrorArray+=(y-(k*x+b))**2 31 return ErrorArray 32 33 ###绘制ErrorArray+最低点### 34 from enthought.mayavi import mlab 35 36 #画整个Error曲面 37 k,b=np.mgrid[k0-1:k0+1:10j,b0-1:b0+1:10j] 38 Err=S(k,b) 39 face=mlab.surf(k,b,Err/500.0,warp_scale=1) 40 mlab.axes(xlabel='k',ylabel='b',zlabel='Error') 41 mlab.outline(face) 42 43 #画最低点（即k，b所在处） 44 MinErr=S(k0,b0) 45 mlab.points3d(k0,b0,MinErr/500.0,scale_factor=0.1,color=(0.5,0.5,0.5)) #scale_factor用来指定点的大小 46 mlab.show()

3 结语

本次博客给出了最小二乘法的Python实现方法，它用到了scipy库中的leastsq函数。在上面我们给出了两个实例，分别实现了对一元一次函数的拟合和一元二次函数的拟合，而事实上，对于函数并不一定得是一元函数，对于更多元的函数也同样能够利用最小二乘法完成拟合工作，不过随着元和次的增加，待求参数也就越来越多了，比方说二元二次函数就有6个待求参数w0~w6。

然为了更好地理解神经网络的训练算法，并不建议直接使用leastsq函数完成对未知参数的求解，因此在以后的博客中我会详细说明如何利用梯度下降法来求解误差函数的最小值。

4 下面要写的博客

1、梯度下降法（什么是梯度下降法，如何使用梯度下降法求一元二次函数最小值，如何使用梯度下降法求二元二次函数的最小值）

2、最小二乘法拟合二元二次函数（即求解w0~w5，相当于对梯度下降法的一个应用）

以上两个内容我会放在同一个博客中。

https://study.163.com/provider/400000000398149/index.htm?share=2&shareId=400000000398149（欢迎关注博主主页，学习python视频资源，还有大量免费python经典文章）
查看全文