Suppose a sorted array is rotated at some pivot unknown to you beforehand.
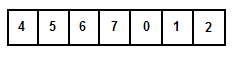
(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
思路:
Point 1
这道题很常见,有三个点需要考虑
1 handle edge case. Thinking about only 2 elements in array.
2 The solution will degrade into O(n) only when there is duplicate elements in array
Searching an Element in a Rotated Sorted Array
For example, for input “1 2 1 1 1 1″, the binary search method below would not work, as there is no way to know if an element exists in the array without going through each element one by one.
3 Merge the 2 steps: find the rotation pivot O( log N) + binary searchO( log N)
举个栗子看看
Look at the middle element (7). Compare it with the left most (4) and right most element (2). The left most element (4) is less than (7). This gives us valuable information — All elements in the bottom half must be in strictly increasing order. Therefore, if the key we are looking for is between 4 and 7, we eliminate the upper half; if not, we eliminate the bottom half.
When left index is greater than right index, we have to stop searching as the key we are finding is not in the array.
Point 2
如果需要进行多次查找,完全可以记下来pivot的地址,那么以后就都可以O(lgn)啦
Point 3
翻了翻题解,发现挺有意思的是brute force在Leetcode OJ上也能Accept,这就要从cache hit rate讲起了:
It is difficult to differentiate between O(n) and O(log n) algorithm in general, as @loick already answered nicely here.
Since the O(n) algorithm traverses the array in sequence, it is extremely fast as the cache hit rate is going to be high.
On the other hand, the O(log n) binary search algorithm has more unpredictable array index access, which means it will result in more cache misses.
Unless n is extremely large (up to billions, which is unpractical in this case), there could be a chance that the Brute Force O(n) algorithm is actually faster.