Good Bye 2017 C. New Year and Curling

Carol is currently curling.

She has n disks each with radius r on the 2D plane.

Initially she has all these disks above the line y = 10¹⁰⁰.

She then will slide the disks towards the line y = 0 one by one in order from 1 to n.

When she slides the i-th disk, she will place its center at the point (x_i, 10¹⁰⁰). She will then push it so the disk’s y coordinate continuously decreases, and x coordinate stays constant. The disk stops once it touches the line y = 0 or it touches any previous disk. Note that once a disk stops moving, it will not move again, even if hit by another disk.

Compute the y-coordinates of centers of all the disks after all disks have been pushed.

Input

The first line will contain two integers n and r (1 ≤ n, r ≤ 1 000), the number of disks, and the radius of the disks, respectively.

The next line will contain n integers x₁, x₂, ..., x_n (1 ≤ x_i ≤ 1 000) — the x-coordinates of the disks.

Output

Print a single line with n numbers. The i-th number denotes the y-coordinate of the center of the i-th disk. The output will be accepted if it has absolute or relative error at most 10^- 6.

Namely, let's assume that your answer for a particular value of a coordinate is a and the answer of the jury is b. The checker program will consider your answer correct if for all coordinates.

Example

Input

6 2
5 5 6 8 3 12

Output

2 6.0 9.87298334621 13.3370849613 12.5187346573 13.3370849613

Note

The final positions of the disks will look as follows:

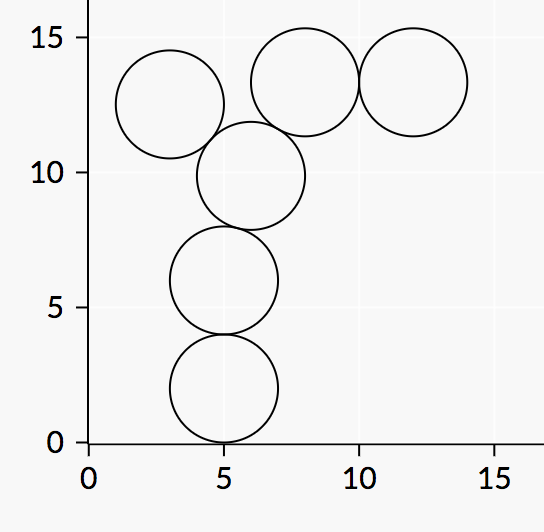
In particular, note the position of the last disk.

题意：

给定半径相等的各个圆圆心横坐标，求每个圆的纵坐标(任意两两之间顶多相邻），注意“The checker program will consider your answer correct if for all coordinates.”

解题思路：

emmmm，为啥当场没写出来，可能是看到几何就畏惧了吧TwT,不过被hack精度的那些是什么鬼....

用res[]记录符合题意的纵坐标

每输入一个横坐标，判断和之前所有横坐标相比，只要有一个能达到相离的条件，令其纵坐标为r..

否则，就是

　　　　xx=fabs(x[pre]-x[next]);

　　　　yy=2*r;

　　　　ret=sqrt(yy*yy-xx*xx)+res[pre];

然后每次取最大值就可以了

具体看代码：

#include <iostream>
#include<cstdio>
#include<cmath>
using namespace std;
double res[1005];
int n,r,x[1005];
double dis(int i,int j)
{
    if(fabs(x[i]-x[j])<=2*r)
    {
        double xx=fabs(x[i]-x[j]);
        double yy=2*r;
        return sqrt(yy*yy-xx*xx)+res[i];
    }
    return r;
}
double solve(int i)
{
    double ret=r;
    for(int j=0;j<i;j++)
        ret=max(ret,dis(j,i));
    return ret;
}
int main()
{
    while(cin>>n>>r)
    {
        for(int i=0;i<n;i++)
        {
            scanf("%d",&x[i]);
            res[i]=solve(i);
        }
        for(int i=0;i<n;i++)
            printf("%.10f%c",res[i],i==n-1?'
':' ');
    }
    return 0;
}