5、给定如表4-9所示的概率模型,求出序列a1a1a3a2a3a1 的实值标签。

解:对序列a1a1a3a2a3a1进行编码:
从概率模型可知:
Fx (0)=0 , Fx (1)=0.2 , Fx (2)= 0.5 , Fx (3)=1
对序列a1a1a3a2a3a1进行编码可以看做是对序列113231进行编码
根据公式
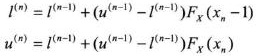
可以确定标签所在区间的上下限。
①将U(0) 初始化为1 ,L(0)初始化为0,该序列的第一个元素为1,得到以下更新:
U(1) =0+(1-0) ×0.2=0.2
L(1) =0+(1-0) ×0=0
故该标签包含在区间[0,0.2)中。
②该序列的第二个元素为1,得到以下更新:
U(2) =0+(0.2-0)× Fx (1)=0.2×1=0.2
L(2) =0+(0.2-0)× Fx (0)=0.2 ×0=0
故该标签包含在区间[0,0.2)中。
③该序列的第三个元素为3,得到以下更新:
U(3) =0+(0.2-0)× Fx (3)=0.2×1=0.2
L(3) =0+(0.2-0)× Fx (2)=0.2 ×0.5=0.1
故该标签包含在区间[0.1,0.2)中。
④该序列的第四个元素为2,得到以下更新:
U(4) =0.1+(0.2-0.1)× Fx (2)= 0.1+0.1×0.5=0.15
L(4) =0.1+(0.2-0.1)× Fx (1)= 0.1+0.1×0.2=0.12
故该标签包含在区间[0.12,0.15)中。
⑤该序列的第四个元素为3,得到以下更新:
U(5) =0.12+(0.15-0.12)× Fx (3)=0.12+0.03×1=0.15
L(5) =0.12+(0.15-0.12)× Fx (2)= 0.12+0.03 ×0.5=0.135
故该标签包含在区间[0.135,0.15)中。
⑥该序列的第五个元素为1,得到以下更新:
U(6) =0.135+(0.15-0.135)× Fx (1)=0.135+0.015×0.2=0.138
L(6) =0.135+(0.15-0.135)× Fx (0)= 0.135+0.015 ×0=0.135
故该标签包含在区间[0.135,0.138)中。
如果以区间中点作为标签,则根据公式
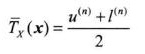
得

因此,序列a1a1a3a2a3a1的实值标签为0.1365。
6、对于表4-9所示的概率模型,对于一个标签为0.63215699的长度为10的序列进行解码。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
// 1.cpp : Defines the entry point for the console application.//#include "stdafx.h"#include<iostream>using namespace std;#define length 11int main(){ double u[11],l[11],F[4]; u[0]=1;l[0]=0; F[0]=0;F[1]=0.2;F[2]=0.5;F[3]=1; double tag=0.63215699; cout<<"标签为0.63215699的长度为10的序列的解码为:"<<'
'; for(int x=1;x<length;x++) { for(int n=1;n<4;n++) { l[x]=l[x-1]+(u[x-1]-l[x-1])*F[n-1]; u[x]=l[x-1]+(u[x-1]-l[x-1])*F[n]; if(tag>=l[x]&&tag<u[x]) { cout<<'a'<<'['<<n<<']'; break; } } } cout<<'
'; return 0;} |
