一、树的定义
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。
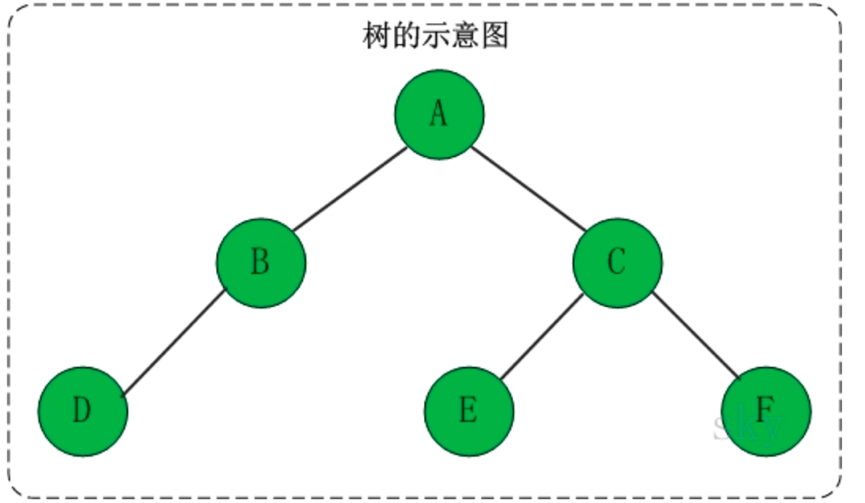
树具有的特点有:
(1)每个结点有零个或多个子结点
(2)没有父节点的结点称为根节点
(3)每一个非根结点有且只有一个父节点
(4)除了根结点外,每个子结点可以分为多个不相交的子树。
树的基本术语有:
若一个结点有子树,那么该结点称为子树根的“双亲”,子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
结点的度:结点拥有的子树的数目
叶子结点:度为0的结点
分支结点:度不为0的结点
树的度:树中结点的最大的度
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1
树的高度:树中结点的最大层次
森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
二、二叉树
1、二叉树的定义
二叉树是每个结点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
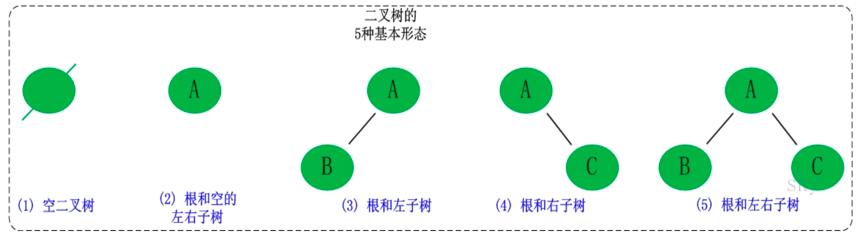
2、二叉树的性质
性质1:二叉树第i层上的结点数目最多为2i-1(i>=1)
性质2:深度为k的二叉树至多有2k-1个结点(k>=1)
性质3:包含n个结点的二叉树的高度至少为(log2n)+1
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
3、性质4的证明
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:因为二叉树中所有结点的度数均不大于2,不妨设n0表示度为0的结点个数,n1表示度为1的结点个数,n2表示度为2的结点个数。三类结点加起来为总结点个数,于是便可得到:n=n0+n1+n2 (1)
由度之间的关系可得第二个等式:n=n0*0+n1*1+n2*2+1即n=n1+2n2+1 (2)
(关于2等式的理解,由于每一个节点都有一个指向它的树干除了根节点,节点数n=树干数+1=n0*0+n1*1+n2*2+1)
将(1)(2)组合在一起可得到n0=n2+1
三、满二叉树、完全二叉树和二叉查找树
1、满二叉树
定义:高度为h,并且由2h-1个结点组成的二叉树,称为满二叉树
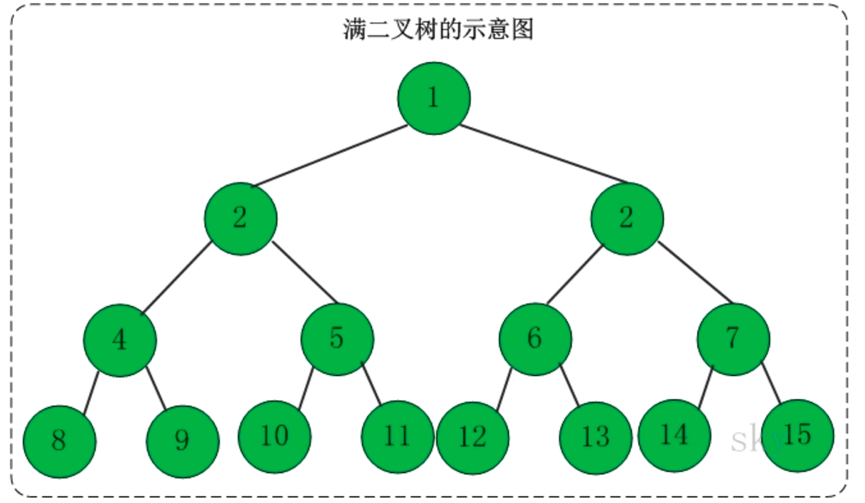
2、完全二叉树
定义:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下层的叶结点集中在靠左的若干位置上,这样的二叉树称为完全二叉树。
特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
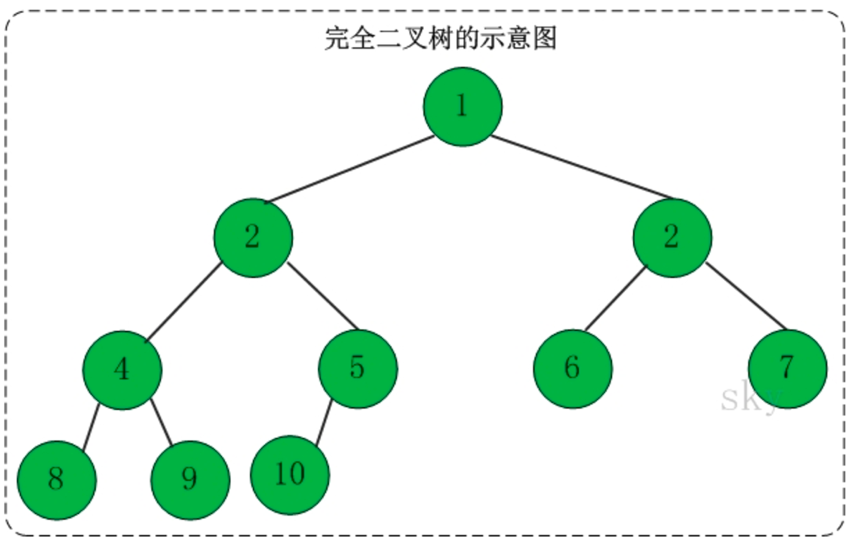
面试题:如果一个完全二叉树的结点总数为768个,求叶子结点的个数。
由二叉树的性质知:n0=n2+1,将之带入768=n0+n1+n2中得:768=n1+2n2+1,因为完全二叉树度为1的结点个数要么为0,要么为1,那么就把n1=0或者1都代入公式中,很容易发现n1=1才符合条件。所以算出来n2=383,所以叶子结点个数n0=n2+1=384。
总结规律:如果一棵完全二叉树的结点总数为n,那么叶子结点等于n/2(当n为偶数时)或者(n+1)/2(当n为奇数时)
3、二叉查找树
定义:二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点,x结点包含关键字key,结点x的key值计为key[x]。如果y是x的左子树中的一个结点,则key[y]<=key[x];如果y是x的右子树的一个结点,则key[y]>=key[x]
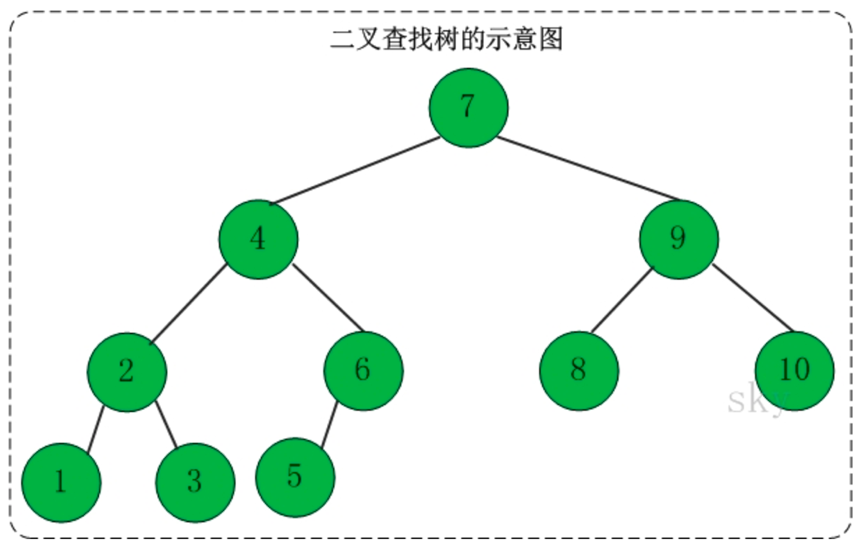
在二叉查找树种:
(1)若任意结点的左子树不空,则左子树上所有结点的值均小于它的根结点的值。
(2)任意结点的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
(3)任意结点的左、右子树也分别为二叉查找树。
(4)没有键值相等的结点。
————————————————
版权声明:本文为CSDN博主「小拳头」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/xiaoquantouer/article/details/65631708