回文的含义是:正着看和倒着看相同,如abba和yyxyy
Manacher算法基本要点:用一个非常巧妙的方式,将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度:在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。 为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,比如$#a#b#a#。
P[id]:以字符str[id]为中心的最长回文串,当以str[id]为第一个字符时,这个最长回文串向右延伸了P[id]个字符。示例:
id: 0 1 2 3 4 5 6 7 8 9 10
str[id]: # a # b # a # c # b #
P[id]: 1 2 1 4 1 2 1 2 1 2 1
这里有一个很好的性质,P[id]-1就是该回文子串在原串中的长度。现在的关键问题就在于怎么在O(n)时间复杂度内求出P数组了。只要把这个P数组求出来,最长回文子串就可以直接扫一遍得出来了。
由于这个算法是线性从前往后扫的。那么当我们准备求P[i]的时候,i以前的P[j]我们是已经得到了的。我们用mx记在i之前的回文串中,延伸至最右端的位置。同时用id这个变量记下取得这个最优mx时的id值。(注:为了防止字符比较的时候越界,我在这个加了‘#’的字符串之前还加了另一个特殊字符‘$’,故我的新串下标是从1开始的)
好,到这里,我们可以先贴一份代码了。
void getMaxPlalinStr(char[] s){
int id = 0; // 记录当前最大回文串的中心位置
int max = 0; // 记录当前最大回文串的最右边界
int len = s.length;
int[] p = new int[len]; // 记录以每个字符为中心的回文串长度
// 线性遍历,求解p[i]
for(int i=0;i<len;i++){
p[i] = max > i ? (p[2*id-i]<(max-i) ? p[2*id-i]:(max-i)) : 1;
while(i-p[i]>=0 && i+p[i]<len && s[i+p[i]]==s[i-p[i]])
p[i]++;
if(p[i]+i > max){
max = p[i]+i;
id = i;
}
}
max = 0;
for(int i=0;i<len;i++){
if(max < p[i]){
max = p[i];
id =i;
}
}
System.out.println("id="+id+",max="+max);
}p[i] = max > i ? (p[2*id-i]<(max-i) ? p[2*id-i]:(max-i)) : 1;
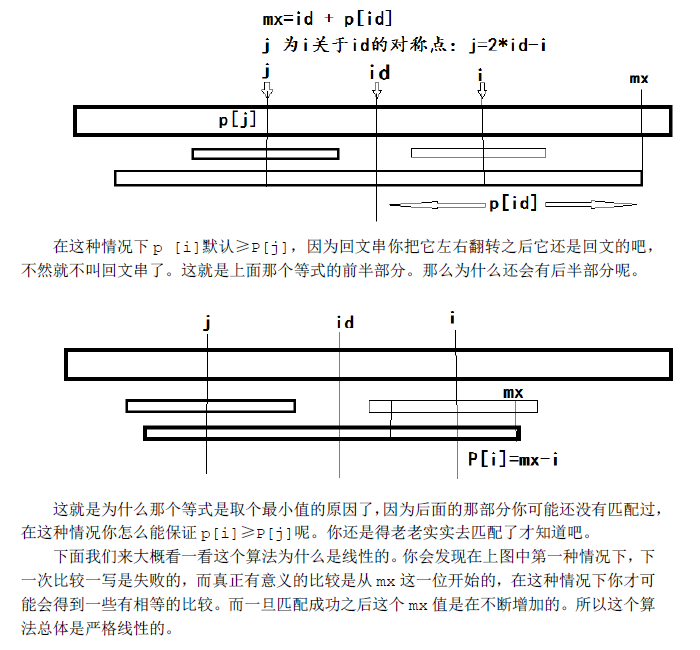
参考:http://blog.csdn.net/ggggiqnypgjg/article/details/6645824