1631. Path With Minimum Effort

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

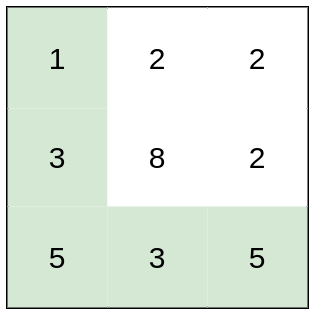
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

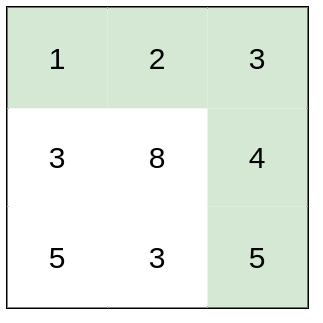
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

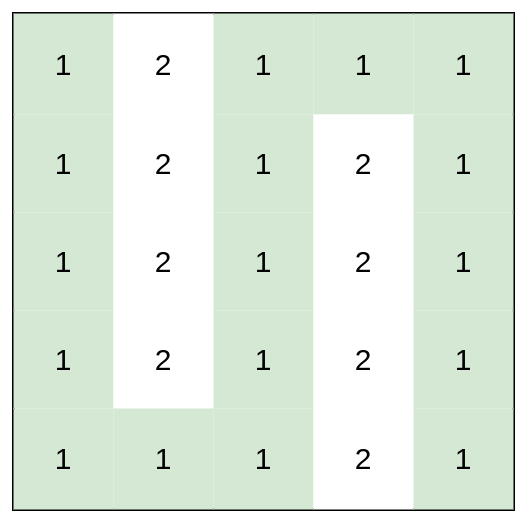
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

class Solution {
    int[] DIR = new int[]{0, 1, 0, -1, 0};
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length, n = heights[0].length;
        int[][] dist = new int[m][n];
        for (int i = 0; i < m; i++) Arrays.fill(dist[i], Integer.MAX_VALUE);
        
        PriorityQueue<int[]> minHeap = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        minHeap.offer(new int[]{0, 0, 0}); // distance, row, col
        while (!minHeap.isEmpty()) {
            int[] top = minHeap.poll();
            int d = top[0], r = top[1], c = top[2];
            if (d > dist[r][c]) continue;
            if (r == m - 1 && c == n - 1) return d; // Reach to bottom right
            for (int i = 0; i < 4; i++) {
                int nr = r + DIR[i], nc = c + DIR[i + 1];
                if (nr >= 0 && nr < m && nc >= 0 && nc < n) {
                    int newDist = Math.max(d, Math.abs(heights[nr][nc] - heights[r][c]));
                    if (dist[nr][nc] > newDist) {
                        dist[nr][nc] = newDist;
                        minHeap.offer(new int[]{dist[nr][nc], nr, nc});
                    }
                }
            }
        }
        return 0; // Unreachable code, Java require to return interger value.
    }
}

https://leetcode.com/problems/path-with-minimum-effort/discuss/909017/JavaPython-Dijikstra-Clean-and-Concise-O(MNlogMN)