摘要
本文主要介绍了数论中的欧拉定理,进而介绍欧拉定理的拓展及应用,结合例题展示如何使用拓展欧拉定理实现降幂取模。
在数论中,欧拉定理,(也称费马-欧拉定理)是一个关于同余的性质定理。了解欧拉定理之前先来看一下费马小定理:
a是不能被质数p整除的正整数,则有a^(p-1) ≡ 1 (mod p)
欧拉给出了推广形式
若n,a为正整数且互质,则 ,其中φ(n)表示小于等于m的数中与n互质的数的数目。可以看出费马小定理是欧拉定理的一种特殊情况。
,其中φ(n)表示小于等于m的数中与n互质的数的数目。可以看出费马小定理是欧拉定理的一种特殊情况。
首先看一个基本的例子。令a = 3,n = 5,这两个数是互素的。比5小的正整数中与5互素的数有1、2、3和4,所以φ(5)=4。计算:a^{φ(n)} = 3^4 =81,而81= 80 + 1 Ξ 1 (mod 5)。与定理结果相符。
然后使用欧拉定理实现简化幂的模运算。比如计算7^{222}的个位数,实际是求7^{222}被10除的余数。7和10[互素],且φ(10)=4。由欧拉定理知7^4Ξ1(mod 10)。所以7^{222}=(7^4)^55*(7^2)Ξ1^{55}*7^2Ξ49Ξ9 (mod 10)。于是该7^{222}的个位数就是9。
最后将欧拉定理拓展到a和m不互质的情况
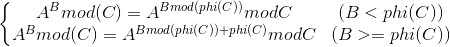
下面给出求解一个φ(n)值的求法:
1 ll euler_phi(ll n) { 2 ll k = (ll)sqrt(n + 0.5); 3 ll ans = n; 4 for(int i = 2; i <= k; i++) { 5 if(n % i == 0) { 6 ans = ans / i * (i - 1); 7 while(n % i == 0) n /= i; 8 } 9 } 10 if(n > 1) ans = ans / n * (n - 1); 11 return ans; 12 }
使用类似筛法的方法计算phi(1),phi(2),phi(3),...phi(n)
1 const int maxn = 100001; 2 ll phi[maxn]; 3 void phi_table(ll n) {//计算1到n的欧拉函数值 4 for(ll i = 2; i <= n; i++) 5 phi[i] = 0; 6 phi[1] = 1; 7 for(ll i = 2; i <= n; i++) { 8 if(!phi[i]) { 9 for(ll j = i; j <= n; j+=i) { 10 if(!phi[j]) phi[j] = j; 11 phi[j] = phi[j] / i * (i - 1); 12 } 13 } 14 } 15 }
可以使用如下代码打印出1 到 10 的phi函数值:

1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 using namespace std; 5 6 typedef long long ll; 7 8 ll euler_phi(ll n) { 9 ll k = (ll)sqrt(n + 0.5); 10 ll ans = n; 11 for(int i = 2; i <= k; i++) { 12 if(n % i == 0) { 13 ans = ans / i * (i - 1); 14 while(n % i == 0) n /= i; 15 } 16 } 17 if(n > 1) ans = ans / n * (n - 1); 18 return ans; 19 } 20 21 const int maxn = 100001; 22 ll phi[maxn]; 23 void phi_table(ll n) {//计算1到n的欧拉函数值 24 for(ll i = 2; i <= n; i++) 25 phi[i] = 0; 26 phi[1] = 1; 27 for(ll i = 2; i <= n; i++) { 28 if(!phi[i]) { 29 for(ll j = i; j <= n; j+=i) { 30 if(!phi[j]) phi[j] = j; 31 phi[j] = phi[j] / i * (i - 1); 32 } 33 } 34 } 35 } 36 37 int main() 38 { 39 40 for(ll i = 1; i <= 10; i++) 41 printf("%I64d ", euler_phi(i)); 42 puts(""); 43 44 phi_table(10); 45 for(ll i = 1; i <= 10; i++) 46 printf("%I64d ", phi[i]); 47 puts(""); 48 return 0; 49 }
看一道例题:FZU 1759 Super A^B mod C
题意
计算A^B mod C,其中1<=A,C<=1000000000,1<=B<=10^1000000。
解题思路
使用数组读入,循环取余,不用分情况。
1 #include <bits/stdc++.h> 2 #define ll __int64 3 using namespace std; 4 5 char a[1000006]; 6 ll x, z; 7 ll quickpow(ll x, ll y, ll z) 8 { 9 ll ans = 1; 10 while(y) 11 { 12 if(y&1) 13 ans = ans * x % z; 14 x = x * x % z; 15 y >>= 1; 16 } 17 return ans; 18 } 19 ll phi(ll n) 20 { 21 ll i, rea = n; 22 for(i = 2; i * i <= n; i++) 23 { 24 if(n % i == 0) 25 { 26 rea = rea - rea / i; 27 while(n % i == 0) 28 n /= i; 29 } 30 } 31 if(n > 1) 32 rea = rea-rea/n; 33 return rea; 34 } 35 int main() 36 { 37 while(scanf("%lld %s %lld",&x,a,&z) != EOF) 38 { 39 ll len = strlen(a); 40 ll p = phi(z); 41 ll ans = 0; 42 for(ll i = 0;i < len; i++) 43 ans = (ans*10 + a[i]-'0')%p; 44 ans += p; 45 printf("%lld ", quickpow(x, ans, z)); 46 } 47 return 0; 48 }
