Rigid Frameworks (画图二分图规律 + DP + 数学组合容斥)

题意：方格n*m，然后对于每一个格子有3种画法1左对角线2右对角线3不画，求让图形稳定的画法有多少种？

思路：通过手画二分图可以发现当二分图联通时改图满足条件，然后我们对于一个dp[n][m]可以利用容器原理先得到所有情况，然后减去不满足情况，那么以一点为中心，假设该点所在的连通块为dp[i][j]那么这时候我们把这些点先用组合数学求出所在连通块对应的组合方式有多少种，然后再是剩下的其余个点随便连都无所谓只要不连接进我原所在连通块就好了。那么我们可以推出式子

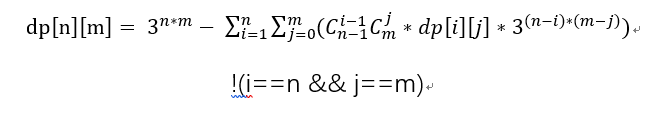
#include<bits/stdc++.h>
using namespace std;

const int mod = 1e9 + 7;
long long dp[12][12];
long long Th[107];
long long in[18];

long long C(int n,int m){
    if(m > n) return 0;
    if(m == 0 || n == 0) return 1;
    return in[n] / in[m] / in[n - m];
}

void init(){
    in[1] = in[0] = Th[0] = 1;
    for(int i = 1; i < 107; i ++) Th[i] = Th[i - 1] * 3 % mod;
    for(int i = 2; i < 17; i ++) in[i] = in[i - 1] * i;

    for(int I = 1; I < 11; I ++)
    for(int J = 0; J < 11; J ++){
        dp[I][J] = Th[I * J];
        for(int i = 1; i <= I; i ++)
        for(int j = 0; j <= J; j ++){
            if(I == i && J == j) continue;
            dp[I][J] -= C(I - 1, i - 1) * C(J, j) *  dp[i][j] % mod * Th[(I - i)*(J - j)] % mod;
            ((dp[I][J] %= mod) += mod) %= mod;
        }
    }dp[1][0] = 0;
}

int main(){
    init();
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        printf("%lld
",dp[n][m]);
    }
    return 0;
}