1.8均摊复杂度和防止复杂度的震荡

关于上一节中我们对添加操作的时间复杂度归结为O(n)是考虑了扩容操作(resize)在内的。就addLast(e)操作而言，时间复杂度为O(1)，在考虑最坏情况下，每次添加均会触发扩容操作，需要移动n个元素，因此此时addLast操作的时间复杂度为O(n)。

（1）addLast(e)均摊时间复杂度分析

resize(n)   O(n)

 假设当前capacity=8，并且每一次添加操作都使用addLast方法

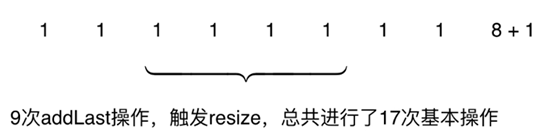
17次基本操作包括：9次添加操作，8次转移操作。均摊每次addLast操作进行大约两次基本操作:

平均值为：17/9≈ 2。

  假设capacity=n，n+1次addLast操作，触发resize，总共进行了2n+1=（n+1）+ n次基本操作；

  均摊每次addLast操作进行大约两次基本操作：

平均值为： 2n+1 / n+1 ≈ 2

结论：因此addLast均摊时间复杂度为O(1)，均摊时间复杂度会比最坏情况有意义，因为一般情况下resize不会每一次都会触发，因此可以分摊到其他上面。
同理，removeLast操作均摊时间复杂度也是O(1)

 （1）addLast(e)和removeLast(e)复杂度震荡分析

设数组的容量为n，此时数组中的个数为n个，此时我们向数组中添加一个元素，则会触发扩容操作；然后在从数组中删除一个元素时又会重新触发缩容操作，这样反复执行都会耗费O(n)的复杂度，导致复杂度震荡。

演示如下：

  第一次执行addLast(e)时间复杂度：O(n)

   第二次执行removeLast(e)时间复杂度：O(n)

  第三次执行addLast(e)时间复杂度：O(n)

   第四次执行removeLast(e)时间复杂度：O(n)

产生复杂度震荡的原因为：removeLast时resize过于着急（Eager）。

解决办法为：Lazy（remove延迟执行resize）

  容量2n，size=n+1时：

 

 容量2n，size=n时，进行缩容1/2：

 容量2n，size=1/4*2n，进行缩容1/2  ：

当size==capacity/4时，才将capacity减半。

现在我们来进一步改进我们的程序代码：

   //从数组中删除index位置的元素，返回删除的元素
    public E remove(int index) {
        //1.判断索引的选择是否合法
        if (index < 0 || index > size)
            throw new IllegalArgumentException("您选择的位置不合法");

        //2.先存储需要删除的索引对应的值
        E ret = data[index];

        //将索引为index之后（index）的元素依次向前移动
        for (int i = index + 1; i < size; i++) {
            //3.执行删除--实质为索引为index之后（index）的元素依次向前移动，将元素覆盖
            data[i - 1] = data[i];
        }
        //4.维护size变量
        size--;
        // loitering objects != memory leak 手动释放内存空间
        data[size] = null;

        //缩容操作
        if (size == data.length / 4 && data.length != 0) {
            resize(data.length / 2);
        }
        //5.返回被删除的元素
        return ret;
    }

 到此我们完成了一个比较完善的动态数组的封装。