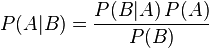1、学习笔记
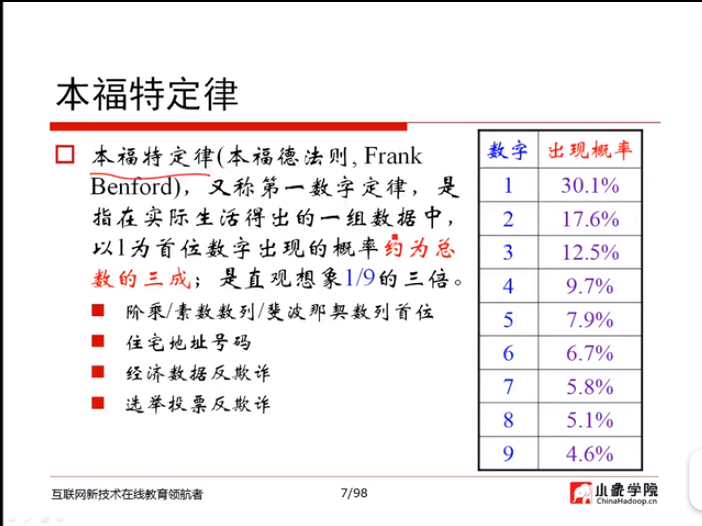
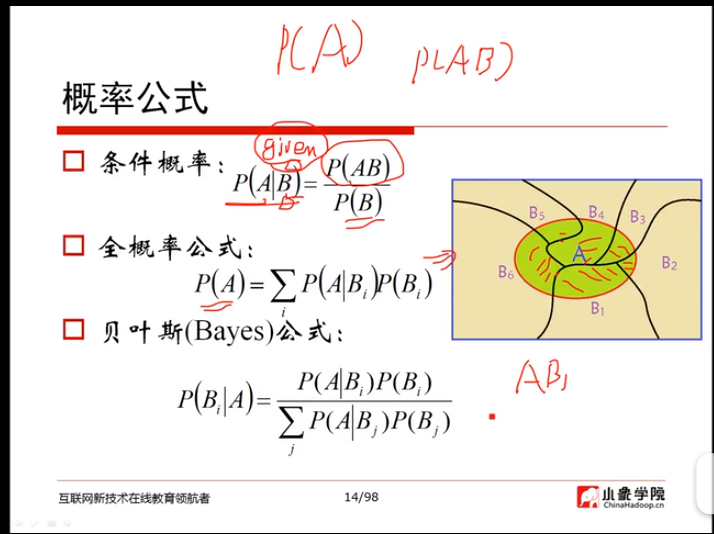
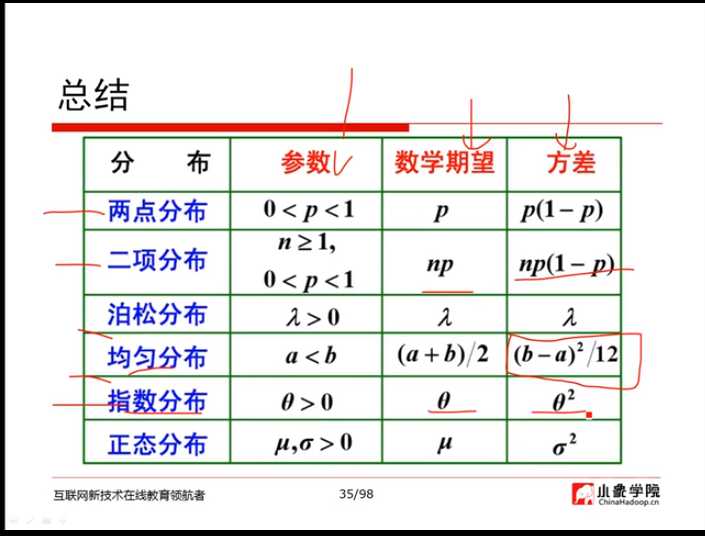
(1)概率论与贝叶斯













(2)矩阵和线性代数









2、用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”。
(1)梯度:
梯度可以定义为一个函数的全部偏导数构成的向量(这一点与偏导数与方向导数不同,两者都为标量)。表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大。
(2)梯度下降:
梯度下降简单来说是一种基于搜索的最优化方法。很多算法都没有闭式解的,所以需要通过一次一次的迭代来找到找到一组参数能让我们的损失函数最小。
(3)贝叶斯定理:
贝叶斯定理是用来描述两个条件概率之间关系的定理,比如P(A|B)和P(B|A),通常,事件A在事件B发生的条件下的概率{P(A|B)}与事件B在事件A的条件下的概率{P(B|A)}是不一样的,但是这两者之间有确定的关系,贝叶斯法则就是这种关系的陈述。