UESTC 881 神秘绑架案 --二维DP

LRJ黑书上的例题。

化简均方差公式：

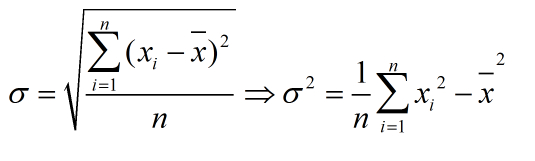
均值的平方一定，所以只需让矩形的总分的平方和最小即可。

定义：dp[k][x1][y1][x2][y2]，以(x1,y1)为左上角坐标，(x2,y2)为右下角坐标的矩形，切割K次以后得到的k+1块举行的总分平方和的最小值

转移方程：（分成横割和竖割）

dp[k][x1][y1][x2][y2]=min{ dp[k-1][x1][y1][a][y2]+sum[a+1][y1][x2][y2], dp[k-1][a+1][y1][x2][y2]+sum[x1][y1][a][y2], (横着 x1≤a＜x2)

dp[k-1][x1][y1][x2][b]+sum[x1][b+1][x2][y2], dp[k-1][x1][b+1][x2][y2]+sum[x1][y1][x2][b] (竖着 y1≤b＜y2) }

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define Mod 1000000007
using namespace std;
#define N 2100

double dp[17][9][9][9][9],sum[9][9][9][9],mp[9][9];

double SUM2(int i,int j,int a,int b)
{
    if(sum[i][j][a][b] >= 0)
        return sum[i][j][a][b];
    double res = 0;
    int k,h;
    for(k=i;k<=a;k++)
        for(h=j;h<=b;h++)
            res += mp[k][h];
    sum[i][j][a][b] = res*res;
    return sum[i][j][a][b];
}

double solve(int k,int i,int j,int a,int b)
{
    if(k == 1)
        return SUM2(i,j,a,b);
    if(dp[k][i][j][a][b] >= 0)
        return dp[k][i][j][a][b];
    double Min1 = Mod;
    double Min2 = Mod;
    for(int s=i;s<a;s++)
        Min1 = min(Min1,min(solve(k-1,i,j,s,b)+SUM2(s+1,j,a,b),solve(k-1,s+1,j,a,b)+SUM2(i,j,s,b)));
    for(int h=j;h<b;h++)
        Min2 = min(Min2,min(solve(k-1,i,j,a,h)+SUM2(i,h+1,a,b),solve(k-1,i,h+1,a,b)+SUM2(i,j,a,h)));
    dp[k][i][j][a][b] = min(Min1,Min2);
    return dp[k][i][j][a][b];
}

int main()
{
    double SUM,AX;
    int i,j,n;
    SUM = 0;
    scanf("%d",&n);
    for(i=1;i<=8;i++)
    {
        for(j=1;j<=8;j++)
        {
            scanf("%lf",&mp[i][j]);
            SUM += mp[i][j];
        }
    }
    AX = SUM/(double)n;
    AX *= AX;
    memset(sum,-1,sizeof(sum));
    memset(dp,-1,sizeof(dp));
    printf("%.3lf
",sqrt(solve(n,1,1,8,8)/(double)n-AX));
    return 0;
}