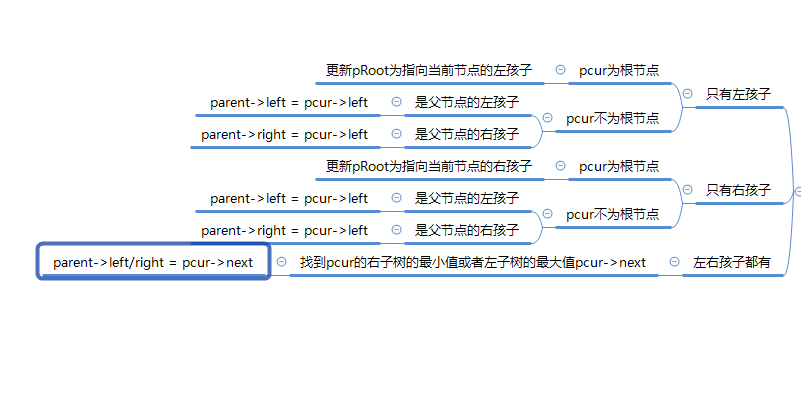
概念
二叉搜索树(Binary Search Tree),又称二叉排序树,它或者是一颗空树,或者具有如下性质的树:
1.若它的左子树不为空。则左子树上所有节点的值都小于根节点的值
2.若它的右子树不为空,则右子树上的所有节点的值都大于根节点的值
3.它的左右子树也分别为二叉搜索树
1.基本操作
1.1 插入
向二叉搜索树中插入新元素时,必须先检测这个元素是否在树中已经存在。如果已经存在,则不进行插入,如果元素不存在则将新元素插入到搜索停止的时候,也就是每次插入都是一个叶子节点。
1.2 查找
在一棵不为空的二叉搜索树中查找元素时,如果要查找的元素与根节点的值相等,则返回true 或根节点,如果小于根节点的值,则在左子树查找,如果大于根节点的值,在其右子树中查找。否则,返回false或者NULL。
1.3 删除
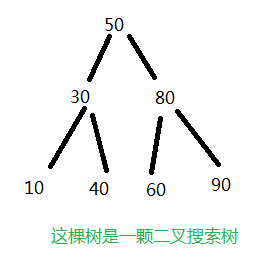
相对查找和插入操作来说,删除算是二叉搜索树中最复杂的一个操作。我们需要分情况讨论。
首先判断是否是一颗空树,是空树则直接返回false,表示删除失败,否则进行下一步
判断当前树是否只有一个结点,且比较要删除的值与根节点的值是否相同,相同则删除成功,不相同,表示删除失败
这里我们将叶子结点进行了归并,总共分为下面三种情况: