定义:
如果图中从V到W有一条有向路径,则V一定排在W之前。满足此条件的顶点序列成为一个拓扑序。
获得一个拓扑序的过程就是拓扑排序。
AOV(网络)如果有合理的拓扑序,则必定是有向无环图(Directed Acyclic Graph, DAG)
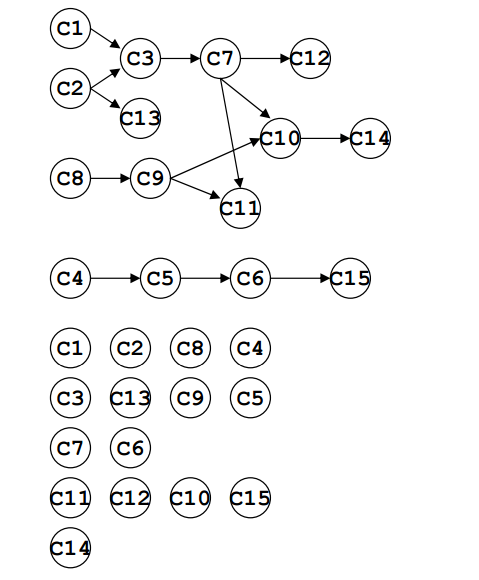

代码:
//邻接表存储 bool TopSort(LGraph Graph, Vertex TopOrder[]) { int InDegree[MaxVertexNum], cnt; Vertex V; PtrToAdjVNode W; Queue Q = CreatQueue(Graph->Nv); //初始化Indegree[] for (V = 0; V < Graph->Nv; V++) InDegree[V] = 0; //遍历图,得到Indegree[] for (V = 0; V < Graph->Nv; V++) for (W= Graph->G[V].FirstEdge; W; W=W->Next) InDegree[W->AdgV]++; //将所有入度为0的顶点入列 for (V = 0; V < Graph->Nv; V++) if (InDegree[V] == 0) AddQ(Q, V); //拓扑排序 cnt = 0; while (!IsEmpty(Q)) { V = DeleteQ(Q); //弹出一个度为0的元素 TopOrder[cnt++] = V; //对V的每个邻接点W->AdjV for (W = Graph->G[V].FirstEdge; W; W=W->Next) if (--InDegree[W->AdjV] == 0) AddQ(Q, W->AdjV); } if (cnt != Graph->Nv) return false //图中有回路 else return true; }