Codeforces 798C

C. Mike and gcd problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike has a sequence A = [a1, a2, ..., an] of length n. He considers the sequence B = [b1, b2, ..., bn] beautiful if the gcd of all its elements is bigger than 1, i.e. .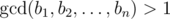

Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index i (1 ≤ i < n), delete numbers ai, ai + 1 and put numbers ai - ai + 1, ai + ai + 1 in their place instead, in this order. He wants perform as few operations as possible. Find the minimal number of operations to make sequence A beautiful if it's possible, or tell him that it is impossible to do so.

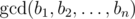 is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).

Input

The first line contains a single integer n (2 ≤ n ≤ 100 000) — length of sequence A.

The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.

Output

Output on the first line "YES" (without quotes) if it is possible to make sequence A beautiful by performing operations described above, and "NO" (without quotes) otherwise.

If the answer was "YES", output the minimal number of moves needed to make sequence A beautiful.

Examples

input

2
1 1

output

YES
1

input

3
6 2 4

output

YES
0

input

2
1 3

output

YES
1

Note

In the first example you can simply make one move to obtain sequence [0, 2] with .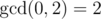

In the second example the gcd of the sequence is already greater than 1.

题目大意：能否能找到最小的操作次数，使得gcd(b1,b2,...,bn)>1 。如果能，输出YES和最小操作次数，否则输出NO。

思路提示：首先，肯定能。

　　　　　证明：假设b[i]和b[i+1]都为奇数，经过一次操作变换为b[i]-b[i+1]和b[i]+b[i+1]都是偶数（2的倍数）；

　　　　　　　　假设b[i]和b[i+1]为一奇数一偶数，经过两次操作变换为2b[i]和-2b[i+1]都是偶数；

　　　　　　　　所以，可以经过有限次操作，使得gcd(b1,b2,...,bn)=2。

方法：

　　先计算gcd(b1,b2,...,bn),如果大于1，输出YES和0；

　　否则：

　　先把所有b[i]和b[i+1]都为奇数的经过一次变换为偶数，记录操作次数，再把b[i]和b[i+1]为一奇数一偶数的经过两次变换为偶数，记录操作次数。

　　最后，输出总的操作次数。

代码：

#include<iostream>
#include<cstdio>
using namespace std;
#define ll long long
const int N=1e5+5;
ll gcd(ll x,ll y)
{
    while(y^=x^=y^=x%=y);
    return x; 
}
int a[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin>>n;
    int cnt=0;
    int gd;
    for(int i=0;i<n;i++)
    {
        cin>>a[i]; 
        if(i!=0)gd=gcd(gd,a[i]);
        else gd=a[i];
    } 
    if(gd>1)
    {
        cout<<"YES"<<endl,cout<<0<<endl;
        return 0;
    }
    for(int i=0;i<n-1;i++)
    {
        if(a[i]&1&&a[i+1]&1)
        cnt++,a[i]=a[i+1]=2;
    }
    for(int i=0;i<n-1;i++)
    {
        if((a[i]&1&&a[i+1]%2==0)||(a[i]%2==0&&a[i+1]&1))
        cnt+=2,a[i]=a[i+1]=2; 
    }
    cout<<"YES"<<endl;
    cout<<cnt<<endl;
    return 0;
}