2018年全国多校算法寒假训练营练习比赛（第一场）D N阶汉诺塔变形

https://www.nowcoder.com/acm/contest/67/D

思路：

先手动模拟一下过程，以下是模拟过程，按顺序表示第几步需要移动的盘标号

1 1 2 1 1 2

1 1 3 1 1 2

1 1 2 1 1 3

1 1 2 1 1 2

1 1 4 1 1 2

。。。。。。

我们发现每出现两次1就会出现一次2，每两次2就会出现一次3，每两次3就会出现一次4，每两次4就会出现一次5。。。。。。

然后我们发现如果把所有大于1的标号看成1，那么k步1出现的次数是 k/1

　　　　　　如果把所有大于2的标号看成2，那么k步2出现的次数是 k/3　　

　　　　　　如果把所有大于3的标号看成3，那么k步3出现的次数是 k/3^2

　　　　　　如果把所有大于4的标号看成4，那么k步4出现的次数是 k/3^3　　

　　　　　　。。。。。。

那么为什么可以这样呢

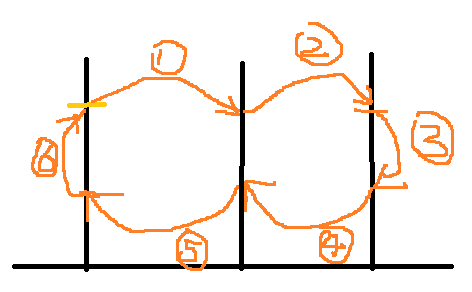
因为这样我们就可以把移动的循环看成6步，刚才说过每出现两次i,出现一下i+1,所以每移动两步停一下（如图③和⑥过程），所以k/3^(i-1)可以表示通过这个循环的步数，取余6就知道i走到哪里了

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
vector<int>a[3];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    ll n,k;
    while(cin>>n>>k){
        for(int i=0;i<3;i++)a[i].clear();
        ll base=1;
        for(int i=1;i<=n;i++){
            int t=(k/base)%6;
            if(t>2)t=5-t;
            a[t].pb(i);
            base*=3;
        }
        for(int i=0;i<3;i++){
            if(a[i].size()) for(int j=a[i].size()-1;j>=0;j--)cout<<a[i][j]<<(j==0?'
':' ');
            else cout<<0<<endl;
        }
    }
    return 0;
}