【LeetCode & 剑指offer 刷题笔记】目录(持续更新中...)
Unique Paths(系列)
Unique Paths
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
_files/Image.png)
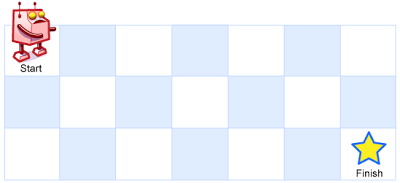
Above is a 7 x 3 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
Example 2:
Input: m = 7, n = 3
Output: 28
//问题:街区路径问题(与LCS最长公共子序列问题类似) 求机器人从起点到终点的路径数量
//方法一:设P[i][j] 为到坐标(i,j)的路径总数,则由于机器人只能向右或者向下,故有P[i][j] = P[i - 1][j] + P[i][j - 1]
//O(n^2) O(m*n)
class Solution
{
public:
int uniquePaths(int m, int n)
{
vector<vector<int>> path(m, vector<int>(n, 1)); //(1,0)和(0,1)处初始化为1
for(int i = 1; i<m; i++) //i从1开始,扫描行
for(int j =1; j<n; j++) //扫描列
path[i][j] = path[i-1][j] + path[i][j-1];
return path[m-1][n-1];
}
};
/*
* 方法一改进
用一个列向量存当前需要的元素即可,将空间复杂度优化至O(min(m,n))
* 例子
1 1 1 1 1 1
1 2 3 4 5 6
1 3 6 10 15 21
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
dp[i][j],dp[i-1][j] ---> dp[j]
dp[i][j-1] ---> dp[j-1]
*/
class Solution
{
public:
int uniquePaths(int m, int n)
{
vector<int> dp(n, 1); //进一步改进可以选择min(m,n)
for (int i = 1; i < m; ++i) //扫描行
{
for (int j = 1; j < n; ++j) //扫描列
{
dp[j] += dp[j - 1];
}
}
return dp[n - 1];
}
};
63. Unique Paths II
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as 1 and 0 respectively in the grid.
Note: m and n will be at most 100.
Example 1:
Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
/*
问题:有障碍物的栅格中,机器人从起始点到终点的路径数量
方法:动态规划
对于有障碍物的栅格中,dp值置0
*/
class Solution
{
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
{
if (obstacleGrid.empty() || obstacleGrid[0].empty() || obstacleGrid[0][0] == 1)
return 0; //矩阵为空或者起始点为障碍点时,退出
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n)); //初始化为0
for (int i = 0; i < m; i++) //从0开始扫描,因为任何点都有可能为障碍点(如(0,1)和(1,0))
{
for (int j = 0; j < n; j++)
{
if (obstacleGrid[i][j] == 1) dp[i][j] = 0; //有障碍的地方dp值置0
else if (i == 0 && j == 0) dp[i][j] = 1; //起始点到起始点路径数为1(若无障碍)
else if (i == 0 && j > 0) dp[i][j] = dp[i][j - 1]; //第一行的处理
else if (i > 0 && j == 0) dp[i][j] = dp[i - 1][j]; //第一列的处理
else dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; //其他情况的处理
}
}
return dp.back().back(); //返回末尾点
}
};