精读80-260程序转弯模板
大家好,我是那个一直在画风螺旋的刘崇军,从今天开始我将尝试运用风螺旋的思考方式,对飞行程序模板展开讨论。希望通过这个系列的文章,能够为大家的模板学习、自动化计算以及软件开发提供一些思路和参考。
今天我将为大家介绍的是反向程序中的80-260程序转弯模板,开始之前,先假定大家对这个模板已经有了一定的了解,手边有ICAO的8168规范或是《仪表飞行程序设计手册》(9368文件),本文中使用的参数和图符标记与ICAO文件中的用法基本一致。
想要了解一个飞行程序模板,首先应该从模板所代表的飞行方法开始。80-260程序转弯模板就代表了这样的一种飞行方法:沿某航迹方向过a点后,通过5秒的建立坡度时间到达b点,过b点后,开始向一侧转弯80°。转弯完成后到达d点,通过5秒钟恢复姿态,再向另一侧通过5秒钟建立坡度(一共是10秒的直线段飞行),从e点开始进行260°的转弯,最后切入向台航迹进近着陆。整体的轨迹(专业的名称为:标称航迹)如下图所示:

这里关于5秒和10秒的解释,规范中并未提及,通过DOC8168转弯设计参数表中的数值进行比对,只有建立坡度时间与此对应(个人理解,欢迎拍砖)。
受风力、机械、设备精度等原因影响,标称航迹是难以精确做到的。因此,需要在航空器的运动过程中,对可能存在的轨迹进行分析。比如,在直线运动时,需要考虑5°的航向容差。这个容差代表着5°以内都可以被认为是标称航迹。因此,在10秒钟直线飞行的de段两侧可以分别标出最大5°的偏移轨迹,当做是最大可能的存在偏移的标称航迹。如下图所示:

由于5°的角度实大太小,所以上图中本应标注的d1、d2在图中未能列出。用偏差5°的直线段去与前一段80°转弯的圆弧相切(平滑衔接),则可以知道,它们的切点分别位于75°转弯点和85°转弯点处(分别位于d点的前后,非常接近d点但不是d点)。
在各自的5°偏移航迹上飞行10秒钟之后,开始进行260°的大转弯,各自的转弯圆心分别是上图中的 f1 和 f2。以 f2 为圆心的转弯弧上依次分布有 g、h、i、j 四点,以 f1 为圆心的转弯弧上依次分布有k、l、m 三个点,各点之间的间隔为45°。k 点是 从 e1 点开始转弯180°后的位置,所在 k 点在计算风偏移量时是按照 75+180 =255°来计算的。
传统的模板绘制方法是在假定的两条标称航迹上分段绘制圆弧,最后用包络线的方式,形成螺旋形的外边界。
风螺旋的计算方法中更关注风螺旋的起点条件,因为,公切线的位置与风螺旋的初始条件紧密相关。
我们通过下图来详细分析一下80-260模板中风螺旋的初始条件。
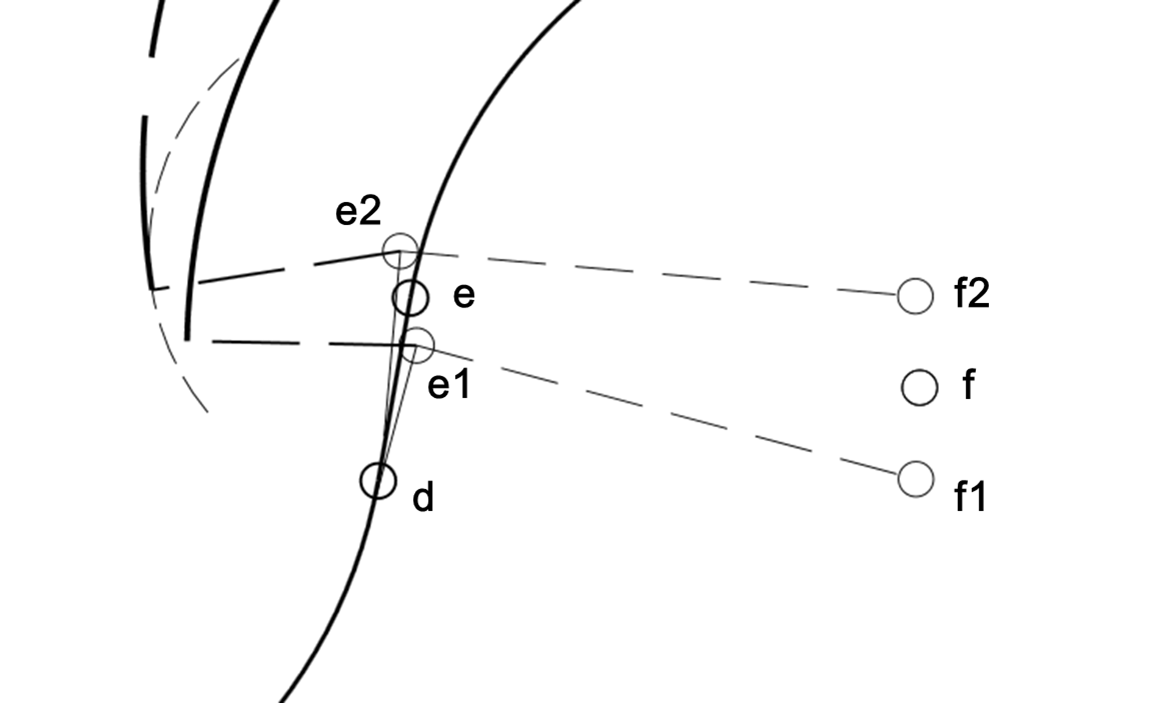
风螺旋基础参数有三个:圆心点位置、初始旋转角度、初始外扩距离。
f1圆心点的坐标计算路径:从a点向右移动5v距离(v是以 km/秒 为单位的真空速 )至达b 点,左转90度移动 r (转弯半径的长度)到达c 点,再右转105度移动r 至 d1点,从d1点左转90°,移动10v至达e1点,右转90°移动r 到达f1 位置点。f2 圆心点的计算方法与此相近,只是 c 点出发时转弯为95°。
x 坐标向右为正,y坐标向下为正,角度顺时针增大的情况下(软件系统中通常采用这种设置),IAS 405km/h,Altitude 1850m,风速12h+87情况下,f1的坐标为(x:7685,y:-2898),f2 的坐标为(x:7679,y:-4132)。f1 与 f2 之间的距离为 1234m,从 f1 指向 f2 的角度为 89.7°。
若以水平向右为零度轴,顺时针角度增大,则可以知道,f1 风螺旋的初始 rotation 为195°,f2 风螺旋的初始 rotation 为 185°。
飞行程序保护区外边界是按照整个飞行过程中受侧风影响的总和来计算的。分别来看 e1 和 e2 点处风力影响的总量是怎样计算的:
e1 点由转弯75°加上15秒(ab段的5秒加上d1e1段的10秒)的直线段飞行而来,它所受的总风偏移量为 75*E + 15*w,E代表每转弯一度所移动的距离,w代表以 km/秒 为单位的风速。(在标准模板参数表中,e1 点的数据被省略了,但 k 点的计算是基于 e1 点的数值)
e2 点由转弯85°加上15秒(ab段的5秒加上d1e1段的10秒)的直线段飞行而来,它所受的总风偏移量为 85*E + 15*w。
e1、 e2 点的风偏移量就是分别以 f1、 f2 为圆心的风螺旋的初始外扩距离(offset)。
两个风螺旋初始条件之差为(终点减去起点,公切线处f1风螺旋在后,因此,用 f1 风螺旋的参数 减去 f2 风螺旋的参数。rotation值越大,则转弯所经过的角度值就越小,通过转弯实现的外扩距离就越少 ):
( 75*E + 15*w)-(85*E + 15*w)-(195-185)*E = -20*E = -290m
若 f1 与 f2 之间的距离为 dist,则风螺旋公切线与 两圆心点连线的夹角等于arcSin(-20*E/dist)= arcSin(-290/1234)= -13.6°。
圆心点连线的角度是已知条件,因而,公切线的角度等于 圆心连线角度减去公切线与连线的夹角:89.7-(-13.6)=103.3°。
公切线处 f1 风螺旋的对应的 sita 角为:
(103.3) - 90+DA - rotation1 = 463.3 - 90 + 13.8 - 195 = 192.1°
公切线处 f2 风螺旋的对应的 sita 角为:
(103.3) - 90+DA - rotation2 = 463.3 - 90 + 13.8 - 185 = 202.1°
也就是说 f1 风螺旋在 E192°时,为最大外边界点, f2 风螺旋在 E202°时,为最大外边界点,这两个外边界点的连线是两条风螺旋的公切线。
对于 f2 风螺旋来说,从E0°至 E202°之间的部分按照风螺旋公式绘制即可。f1 风螺旋从 E192°开始绘制,至E270°即可实现模板的大部分边界。
(特别说明:以上数值仅针对 IAS 405km/h,Altitude 1850m,风速12h+87 的80-260程序转弯模板有效 )
公切线与风螺旋的位置关系,如下图所示:

由于风螺旋精确算法是对原有的分段圆弧画法的数学模拟,因此在上图中可以看到,风螺旋线精确的与分段圆弧相切。从上图中还可以看到过 m 点之后,若继续以风螺旋的方法绘图,保护区边界将会超出现有模板的范围。根据ICAO 9371《 Template manual for holding reversal and racetrack procedures》文件来看,程序转弯的外边界并不一定要收回到a点,因此,不需要刻意的去绘制 a 点与风螺旋的公切线。
按照现有规范标准完整个绘制的80-260模板如下图所示:

图中 角 A 部分是风螺旋的起点转弯至 圆心点连线的角度,角 B 部分是从圆心点连线至公切线的sita角度。
在这张图中用 m 点的圆弧做为模板的结束位置,与规范中的模板看起来一致了,但通过本篇文章,您已经可以知道这个结束位置还是“画小了”。
风螺旋算法是一种用于计算机自动化计算的方法,本文中所列数据均基于特定的软件系统,仅供参考。80-260模板是所有模板中仅用了两条风螺旋搭建起来的模板,因此,在算法分析或是软件实现时,均可以此为起点进行分析研究。标准模板中的分段圆弧画法在这里仅做为参考使用。
与本篇相关的论文发表于2017年4月的《航空计算技术》,论文的引用格式为:
[1] 刘崇军, 赵航. 风螺旋线精确算法在程序转弯模板中的应用[J]. 航空计算技术, 2017, 47(3):62-65.
这篇论文在最后的出版过程中,将80-260模版的最终图片给遗漏了,借本篇文章,刚好补上这张图。