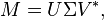奇异值分解是线性代数中一种重要的矩阵分解，在信号处理、统计学等领域有重要应用。奇异值分解在某些方面与对称矩阵或Hermite矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有其相关性，但还是有明显的不同。对称阵特征向量分解的基础是谱分析，而奇异值分解则是谱分析理论在任意矩阵上的推广。
目录 |
理论描述
假设M是一个m×n阶矩阵，其中的元全部属于域 K，也就是 实数域或复数域。如此则存在一个分解使得
其中U是m×m阶酉矩阵；Σ是半正定m×n阶对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解。Σ对角线上的元素Σi,i即为M的奇异值。
常见的做法是为了奇异值由大而小排列。如此Σ便能由M唯一确定了。(虽然U和V仍然不能确定。)
直观的解释
在矩阵M的奇异值分解中
- V的列(columns)组成一套对
的正交"输入"或"分析"的基向量。这些向量是 
的特征向量。 - U的列(columns)组成一套对的正交"输出"的基向量。这些向量是
的特征向量。 - Σ对角线上的元素是奇异值，可视为是在输入与输出间进行的标量的"膨胀控制"。这些是 及 的特征值，并与U和V的行向量相对应。
奇异值和奇异向量, 以及他们与奇异值分解的关系
与特征值分解的联系
几何意义
因为U 和V 向量都是单位化的向量, 我们知道U的列向量u1,...,um组成了Km空间的一组标准正交基。同样，V的列向量v1,...,vn也组成了Kn空间的一组标准正交基(根据向量空间的标准点积法则).
线性变换T: Kn → Km，把向量x变换为Mx。考虑到这些标准正交基，这个变换描述起来就很简单了: T(vi) = σi ui, for i = 1,...,min(m,n), 其中σi 是对角阵Σ中的第i个元素; 当i > min(m,n)时，T(vi) = 0。
这样，SVD理论的几何意义就可以做如下的归纳：对于每一个线性映射T: Kn → Km，T把Kn的第i个基向量映射为Km的第i个基向量的非负倍数,然后将余下的基向量映射为零向量。对照这些基向量，映射T就可以表示为一个非负对角阵。
简化的 SVD
范数
1. 矩阵范数的概念 设A∈Cm×n，定义一个实值函数||A||，若满足：
(1) 非负性：||A||≥0，且||A||=0当且仅当A=0； (2) 齐次性：||aA||=|a| ||A||，a∈C； (3) 三角不等式：||A+B||≤||A||+||B||，A,B∈ Cm×n; (4) 相容性：||AB||≤||A|| ||B||
则称||A||为A的矩阵范数。 例1 设A=(aij)∈Cn×n，则
都是矩阵范数。
定理2：由向量的1-范数、2-范数和∞-范数分别诱导出的矩阵范数分别是
通常依次称为列和范数、谱范数和行和范数。
定理3：谱范数和F-范数都是酉不变范数，即对于任意酉矩阵P和Q，有||PAQ||=||A||。
应用
求伪逆
奇异值分解可以被用来计算矩阵的伪逆。若矩阵 M 的奇异值分解为 M = UΣV * ，那么 M 的伪逆为
其中 Σ+ 是将Σ转置，并将其主对角线上每个非零元素都求倒数得到的。求伪逆通常可以用来求解线性最小平方问题。
平行奇异值模型
把频率选择性衰落信道进行分解.
值域、零空间和秩
矩阵近似值
奇异值分解在统计中的主要应用为主成分分析（PCA），它是一种数据分析方法，用来找出大量数据中所隐含的“模式”,它可以用在模式识别，数据压缩等方面。PCA算法的作用是把数据集映射到低维空间中去。 数据集的特征值（在SVD中用奇异值表征）按照重要性排列，降维的过程就是舍弃不重要的特征向量的过程，而剩下的特征向量张成空间为降维后的空间。
计算 SVD
matlab： [b c d]=svd(A) OpenCV: void cvSVD( CvArr* A, CvArr* W, CvArr* U=NULL, CvArr* V=NULL, int flags=0 )
历史
参见
外部链接
- LAPACK users manual gives details of subroutines to calculate the SVD (see also [1]).
- Applications of SVDon PC Hansen's web site.
- Introduction to the Singular Value Decompositionby Todd Will of the University of Wisconsin--La Crosse.
- Los Alamos group's book chapterhas helpful gene data analysis examples.
- MIT Lectureseries by Gilbert Strang. See Lecture #29 on the SVD.
- Java SVDlibrary routine.
- Java appletdemonstrating the SVD.
- Java scriptdemonstrating the SVD more extensively, paste your data from a spreadsheet.
- Chapter from "Numerical Recipes in C"gives more information about implementation and applications of SVD.
- Online Matrix Calculator Performs singular value decomposition of matrices.
参考文献
- Demmel, J. and Kahan, W. (1990). Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy. SIAM J. Sci. Statist. Comput., 11(5), 873-912.
- Golub, G. H. and Van Loan, C. F. (1996). "Matrix Computations". 3rd ed., Johns Hopkins University Press, Baltimore. ISBN 0-8018-5414-8.
- Halldor, Bjornsson and Venegas, Silvia A. (1997). "A manual for EOF and SVD analyses of climate data". McGill University, CCGCR Report No. 97-1, Montréal, Québec, 52pp.
- Hansen, P. C. (1987). The truncated SVD as a method for regularization. BIT, 27, 534-553.
- Horn, Roger A. and Johnson, Charles R (1985). "Matrix Analysis". Section 7.3. Cambridge University Press. ISBN 0-521-38632-2.
- Horn, Roger A. and Johnson, Charles R (1991). Topics in Matrix Analysis, Chapter 3. Cambridge University Press. ISBN 0-521-46713-6.
- Strang G (1998). "Introduction to Linear Algebra". Section 6.7. 3rd ed., Wellesley-Cambridge Press. ISBN 0-9614088-5-5.