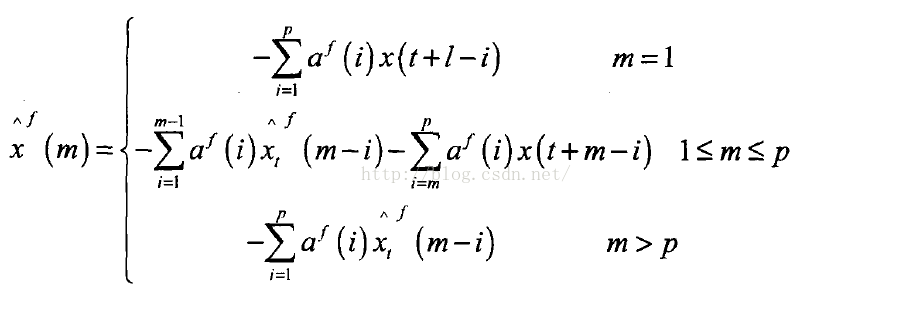憔悴到了转述中文综述的时候了........
在统计学角度来看,时间序列分析是统计学中的一个重要分支, 是基于随机过程理论和数理统计学的一种重要方法和应用研究领域. 时间序列按其统计特性可分为平稳性序列和非平稳性序列. 目前应用最多的是Box一JenkinS 模型建模法, 它是由G.E.P.Box和英国统计学家G.M.JenkinS于1970年首次系统提出的.Box一JenkinS方法是一种较为完善的统计预测方法 , 他们的作用是为实际工作者提供了对时间序列进行分析、预测 , 以用对ARMA模型识别、估计和诊断的系统方法. 优点在于如果建立精确的模型后,并确定模型的系数之后,就可以根据有限的数据集对其发展进行预测 , 其中对于平稳性时间序列多采用ARMA模型 , 对于非平稳性时间序列模型常通过适当地变换 (如差分、取对数) 将它变为ARMA模型后再进行建模,这类模型Box一JenkinS称为ARI琳(求和自回归滑动平均模型) 。
参考链接:时序分析基础
一. 平稳时间序列模型
数据的预处理:
数据的预处理包括缺失值的补充、数据的平稳化及单位根检验.
平稳性
平稳性是时间序列分析中很重要的一个概念。一般的,我们认为一个时间序列是平稳的,如果它同时满足一下两个条件:
1)均值函数是一个常数函数。
2)自协方差函数只与时滞有关,与时间点无关。
以上面两个时间序列为例。两个序列均满足条件1),因为标准正态分布白噪声和其形成的随机游走的均值函数都是值恒为0的常数函数。再来看条件2)。白噪声的自协方差函数可以表述为:
可以看到只有在时滞为0时值为1,其它均为0,所以白噪声是一个平稳序列。
而随机游走我们上面分析过,其自协方差为:
很明显其自协方差依赖于时间点,所以是一个非平稳序列。
后面可以看到,一般的时间序列分析往往针对平稳序列,对于非平稳序列会通过某些变换将其变为平稳的,例如,对于随机游走来说,其一阶差分序列是平稳的(显然其一阶差分是白噪声)。
时序分析主要统计量
注意时间序列中的每一个元素都是一个普通的随机变量,如果忽略序列的时间性,那么我们面对的实际上是一个随机变量集合,所以从这个角度来说时间序列的统计分析与普通统计分析没有太大不同,相关的理论也是通用的。
对于随机变量集合来说,要完整描述其统计特性需要处理其多元联合分布,这是非常复杂的。所以实际我们往往做一些必要的简化假设,避免处理复杂的多元联合分布。
现假设我们有随机时间序列
下面先给出一些常用的统计量。后面会接着通过一些常见序列来举例说明各统计量如何计算。
均值
均值函数被定义为关于自变量t的函数:
t的均值函数值表示在t时刻随机变量
方差
与均值类似,方差是t时刻序列元素的方差:
自协方差
自协方差是一个二元函数,其自变量为两个时间点,值是两个时间点上序列值的协方差:
当t=s时,自协方差就是t时刻的方差。
自相关系数
自相关系数是两个时刻的值的相关系数:
如果忽略元素来自时间序列这一事实,各统计量的意义实际上与普通的统计学中无异。因此这些统计量的一些性质也可以无缝推广到时间序列分析。例如期望的线性性质等等。如果有需要可以自行复习一下这些统计量的相关计算性质。后面的推导会主要集中于这几个统计量的计算。
常见的随机时间序列
常见的随机时间序列有:白噪音、布朗运动(随机游走)、白噪声
考虑一个时间序列,其中每一个元素为独立同分布变量,且均值为0。这种时间序列叫做白噪声。之所以叫这个名字,是因为对这种序列的频域分析表明其中平等的包含了各个频率,和物理中的白光类似。
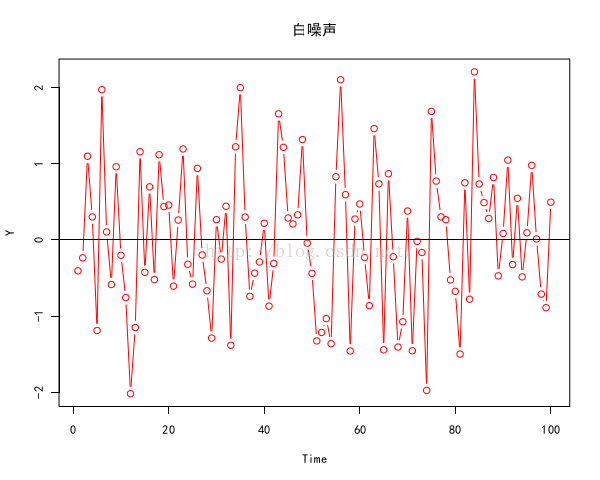
没有模式即是白噪音的模式,所谓的白噪音即是随机性的完全体现,即是不能从白噪音中发现任何模式。以下是一段代码:
Y = ts(rnorm(100, mean=0, sd=1));
plot(Y, family="simhei", main="白噪声", type="b", col="red");
abline(h=0) 其中共100个元素,每个元素都独立服从标准正态分布
由于每个元素服从
白噪声的重要之处在于很多其它的重要时间序列都可以通过它构造出来,这一点下文会看到。我们一般用e表示白噪声,将白噪声序列写作:
布朗运动
下面考虑这样一个时间序列,其在t时刻的值是前面白噪声序列的前t个值之和,设
布朗运动的模式在于其位置是连续曲线,但曲线的处处不可微。

Y = ts(rnorm(100, mean=0, sd=1));
for (i in 2:length(Y)) {
Y[i] = Y[i] + Y[i-1];
}
plot(Y, family="simhei", main="随机游走", type="b", col="red");
abline(h=0)可以看到随机游走比白噪声平滑很多,并且呈现出一些“趋势性”的感觉。下面分析其相关统计特征。
均值:
方差:
对协方差的计算需要用到一个协方差性质:
设t小于s,由于只有i=j时
自协方差:
自相关系数:
从统计性质可以看到,随机游走的“趋势性”实际是个假象,因为其均值函数一直是白噪声的均值,不存在偏离的期望。但是方差与时间呈线性增长并且趋向于无穷大,这意味着只要时间够长,随机游走的序列值可以偏离均值任意远,但期望永远在均值处。
物理与经济学中的很多现象都被看做是随机游走,例如分子的布朗运动,股票的价格走势等等。
从协方差和相关系数看,如果起点t固定,则越接近的点相关性越大,例如
实际上从纯数学角度可以将自相关系数看成一个二元函数,自变量是时间点t和时滞s-t。认识到这点很重要,因为它与时间序列分析中一个重要的概念——平稳性有着密切的关系。
二、AR、MA、ARMA模型
4、AR、MA、ARMA认是平稳时间序列最主要的参数模型. AR模型的正则方程是一组线形方程 ,而MA和ARMA模型是非线性方程.Word分解定理告诉我们任何有限方差的ARMA或MA平移过程可以用可能是无限阶的AR模型表达;同样,任何ARMA或AR模型可以用可能是无限阶的撇模型表达.因此,如果在这三个模型中选一个与信号不匹配的模型,但只要模型的阶足够高,它能够比较好地逼近被建模的随机过程.三种模型中AR模型具有一系列好的性能,因此,是研究最多并获得广泛应用的一种模型。
三、模型用于预测
1.AR(n)模型预测
利用n之前的p个值对x(。)作预测,称之为“前向预测”,记为:
上标f表示前向预测(forwardprediction)·凡(,)表示在t时刻m步前向预测。利用自相关法、Burg算法、协方差、改进的协方差法等方法得到模型的参数后,就可以进行前向预测,利用预测值递推可依次得到多步预测值
2.MA(q)、ARMA(p,q)模型预测
MA(q)、ARMA(p,q)的外推预测一般都是将磁(q)、ARMA(p,q)模型转换为相应的高阶AR模型,再AR模型的预测公式进行外推预测.
3.预测误差
预测误差公式为:
线性最小方差预测的方差和预测步长l有关,而与预测的时间原点t无关.预测 步长l越大,预测误差的方差也越大,因而预测的准确度就会降低.所以一般不能用AR、MA和ARMA模型作为长期预测模型.
四、非平稳时间序列模型