二叉树遍历的应用

1.求二叉树中叶子节点的个数(并打印）

设该树中的叶子数为n0个.该树中的总结点数为n个,则有：

n=n0+n1+n2+…+nK   (1)
n-1=0*n0+1*n1+2*n2+…+K*nK   (2)
联立(1)(2)方程组可得：
叶子数为：n0=1+0*n1+1*n2+2*n3+...+(K-1)*nK

则对二叉树有；n0 = n2+1

就相当于求出了叶子节点n0的数，就知道了这颗二叉树中n1，n2的数目

可以在遍历算法中增加检测条件：左右子树是否都为空

void PreOrder(node *root)
{
    if (root==NULL) return;
    else if (!root->lch&&!root->rch) {
    　　//printf("%c", root->data);
    　　n0++;
    　　PreOrder(root->lch);
    　　PreOrder(root->rch); 
    }
}

2.求二叉树的高度

int depth(node *t)
{
        if(t==NULL) return 0;
        int l = depth(t->lch);
        int r = depth(t->rch);
        return l > r ? l+1 : r+1;
}

3.由两种遍历确定二叉树

必须要有中序遍历才能确定一颗二叉树

以先序和中序遍历序列确定二叉树为例：

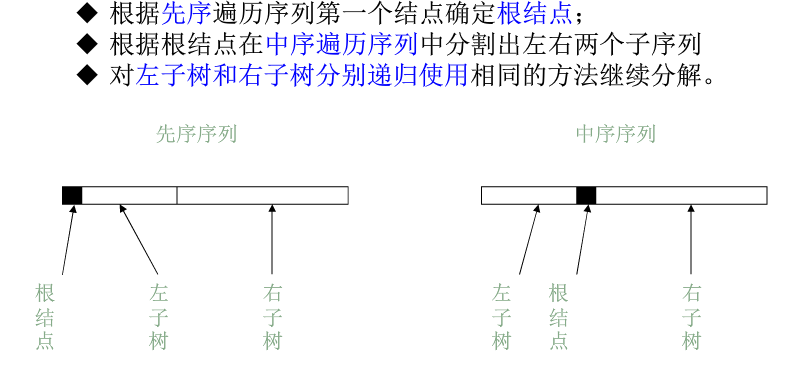
node *create(char *pre, char *in, int num)
{
    if (num==0) return NULL;
    int i = 0;//不要忘了初始化
    while (i<num&&in[i]!=pre[0]) i++;//查找根节点在中序的位置 
    int lnum = i, rnum = num-i-1;
    node *root = (node*)malloc(sizeof(node));
    root->data = pre[0];
    root->lch = create(&pre[1], &in[0], lnum);
    root->rch = create(&pre[i+1], &in[i+1], rnum);
    return root;
} 

后序和中序遍历序列确定二叉树和前面的差不多，有时间我再补上来