第七周
学习目标
知识点描述:应用广泛的二分类算法——逻辑回归
学习目标:
-
逻辑回归本质及其数学推导
-
逻辑回归代码实现与调用
-
逻辑回归中的决策边界、多项式以及正则化
一、初识逻辑回归
1.介绍
1.1 线性回归能解决分类问题么?
其实,线性回归是不能解决分类问题的。因为我们在使用线性回归模型时,我们实际上做了3个假设(实际上有更多的假设,这里只讨论最基本的三个):
- 因变量和自变量之间呈线性相关。
- 自变量与干扰项相互独立。
- 没被线性模型捕捉到的随机因素服从正态分布。
从理论上来说,任何数据放在任何模型里都会得到相应的参数估计,进而通过模型对数据进行预测。但是这并不一定能保证模型效果,有时会得到“错且无用”的模型,因此建模的过程中需要不断提出假设和检验假设。
1.2 用逻辑回归解决分类问题-本质上是一种二分类解决方法
2.算法推导
(计量中的三种二分类:logit回归,probit回归,线性概率回归)
对于一个分类问题,由于“窗口效用”,我们只能看见客户的购买行为,但是在分类的背后,是隐藏变量之间的博弈,我们通过搭建隐藏变量的模型,来求出客户购买的概率。
probit回归在数学上是比较完美的,但是正态分布的累积分布函数,其表达形式很复杂且没有解析表达,因此直接在probit回归上做参数估计是比较困难的。但是好在我们可以对其做近似

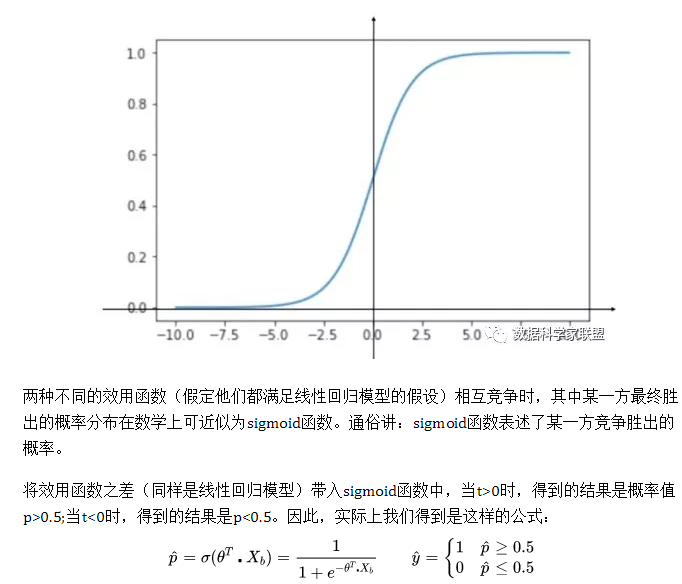
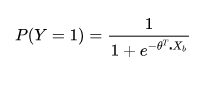
二、从对数几率看逻辑回归
逻辑回归假设数据服从伯努利分布,通过极大似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的。

1.2 面试问题
在有上述的推导之后,再看一个面试问题:
为什么要使用sigmoid函数作为假设?
现在就可以回答了:
因为线性回归模型的预测值为实数,而样本的类标记为(0,1),我们需要将分类任务的真实标记y与线性回归模型的预测值联系起来,也就是找到广义线性模型中的联系函数。如果选择单位阶跃函数的话,它是不连续的不可微。而如果选择sigmoid函数,它是连续的,而且能够将z转化为一个接近0或1的值。
损失函数:
- 如果给定样本的真实类别y=1,则估计出来的概率p越小,损失函数越大(估计错误)
- 如果给定样本的真实类别y=0,则估计出来的概率p越大,损失函数越大(估计错误)

三 逻辑回归代码实现与调用
步骤拆解!
主要内容为:
- 定义sigmoid方法,使用sigmoid方法生成逻辑回归模型
- 定义损失函数,并使用梯度下降法得到参数
- 将参数代入到逻辑回归模型中,得到概率
- 将概率转化为分类
四 分类中的决策边界
1.1决策边界
字面意义

1.3 线性&非线性决策边界
所谓决策边界就是能够把样本正确分类的一条边界,主要有线性决策边界(linear decision boundaries)和非线性决策边界(non-linear decision boundaries)。
注意:决策边界是假设函数的属性,由参数决定,而不是由数据集的特征决定。
2.1 线性回归转换成多项式回归
对于线性这条蓝色的直线可以比较完美地将数据分成两类。但是直线的分类方式,太简单了。

五、sklearn中的逻辑回归中及正则化
在逻辑回归中添加多项式项,从而得到不规则的决策边界,进而对非线性的数据进行很好的分类。但是众所周知,添加多项式项之后,模型会变变得很复杂,非常容易出现过拟合。因此就需要使用正则化,且sklearn中的逻辑回归,都是使用的正则化。
