次小生成树（LCA ）

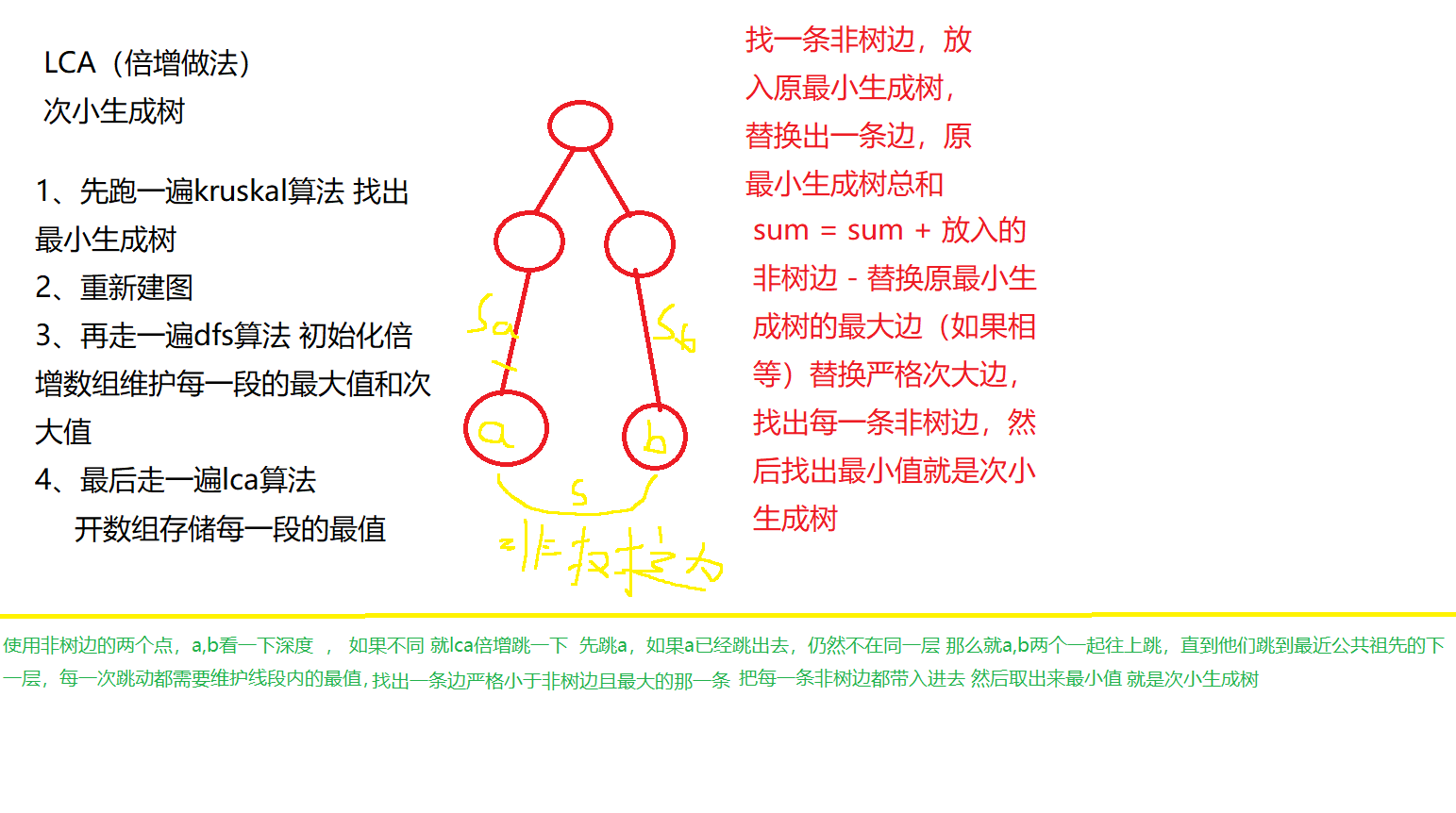
给定一张 N 个点 M 条边的无向图，求无向图的严格次小生成树。

设最小生成树的边权之和为sum，严格次小生成树就是指边权之和大于sum的生成树中最小的一个。

输入格式
第一行包含两个整数N和M。

接下来M行，每行包含三个整数x，y，z，表示点x和点y之前存在一条边，边的权值为z。

输出格式
包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)

数据范围
N≤105,M≤3∗105
输入样例：
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
输出样例：
11

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
const int N = 100010,M=300010,INF = 0x3f3f3f3f;
struct Edge{
    int a,b,w;
    bool ft;
    bool operator <(const Edge & t)const
    {
        return w < t.w; 
    }
    
}edge[M];
int h[N],ne[M],e[M],w[M],idx;
int fa[N][17] , d1[N][17] ,d2[N][17];
int depth[N];
int n , m;
int p[N];
int q[N];
void add(int a,int b ,int c)
{
    e[idx] = b, ne[idx] = h[a] , w[idx] = c , h[a] = idx ++;
}
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
LL kruskal()
{
     sort(edge,edge+m);
    for(int i = 1; i <= n ; i++)p[i] = i;
    LL res = 0 ;
    for(int i = 0 ; i < m ; i++)
    {
        int a = find(edge[i].a) , b = find(edge[i].b), w= edge[i].w;
        if(a != b)
        {
            p[a] = b;
            res += w;
            edge[i].ft = true;
        }
    }
    return res;
}

void bulid()
{
    memset(h,-1,sizeof h);
    for(int i = 0 ; i < m ; i ++)
    {
        int a = edge[i].a , b = edge[i].b , w = edge[i].w;
        if(edge[i].ft)
        {
            add(a,b,w),add(b,a,w);
        }
    }
}

void dfs()
{
    memset(depth,0x3f ,sizeof depth);
    queue<int> q;
    depth[0] = 0 , depth[1] = 1;
    q.push(1);
    
    while(q.size())
    {
        int t = q.front();
        q.pop();
        for(int i = h[t] ; ~i ; i = ne[i])
        {
            int j = e[i];
            if(depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q.push(j);
                fa[j][0] = t;
                d1[j][0] = w[i] , d2[j][0] = -INF;
                for(int k = 1; k <= 16 ;k ++)
                {
                    int anc = fa[j][k-1];
                    fa[j][k] = fa[anc][k-1];
                    int distance[4] = {d1[j][k-1],d2[j][k-1],d1[anc][k-1] , d2[anc][k-1]};
                    d1[j][k] = d2[j][k] = -INF;//两个最值存储
                    for(int u = 0 ; u < 4 ; u ++)
                    {
                        int d = distance[u];
                        if (d > d1[j][k]) d2[j][k] = d1[j][k], d1[j][k] = d;
                        else if (d != d1[j][k] && d > d2[j][k]) d2[j][k] = d;
                    }
                    
                }
                
            }
        }
    }
}

int lca(int a, int b , int w)
{
    static int distance[N * 2];
    int cnt = 0 ;
    if(depth[a] < depth[b])swap(a,b);
    for(int k = 16 ; k >= 0 ;k--)
    {
        if(depth[fa[a][k]] >= depth[b])
        {
            distance[cnt ++] = d1[a][k];
            distance[cnt ++] = d2[a][k];
            a = fa[a][k];
        }
    }
    if(a != b)
    {
        for(int k = 16 ; k >= 0 ; k --)
        
            if(fa[a][k] != fa[b][k])
            {
              
                distance[cnt ++] = d1[a][k];
                distance[cnt ++] = d2[a][k];
                distance[cnt ++] = d1[b][k];
                distance[cnt ++] = d2[b][k];
                //先存进来 
                a = fa[a][k];
                b = fa[b][k];
            }
        
        distance[cnt ++] = d1[a][0];
        distance[cnt ++] = d1[b][0];
        
    }
    int dist1 = -INF , dist2 = -INF;
    for(int i = 0 ; i < cnt ; i ++)
    {
        int d = distance[i];
        if(d > dist1) dist2 = dist1 , dist1 = d;
        else if(d != dist1 && d > dist2) dist2 = d;
    }
    if(w > dist1) return w-dist1;
    if(w > dist2) return w -dist2;
    return INF;
    
}
int main()
{
    cin >> n >> m;
    for(int i = 0 ; i < m ; i++)
    {
        int a ,b ,c;
     scanf("%d%d%d", &a, &b, &c);
        edge[i] = {a,b,c};
    }
    LL sum = kruskal();//返回最小生成树 权值总和
    
    bulid();//建立最小生成树
    dfs();//初始化得到每段最大值和严格次大值
    
    LL res = 1e18;
    
    for(int i  = 0 ; i < m ; i ++)
    {
        if(!edge[i].ft)
        {
             int a = edge[i].a, b = edge[i].b, w= edge[i].w;
            res = min(res,sum + lca(a,b,w));
        }
    }
    printf("%lld
", res);
    
    return 0;
    
}