排序算法：快速排序解析及Python实现

关键词：分而治之、递归、计算速度、基准值

1. 什么是分而治之？

1.1 分而治之（divide and conquer）一种递归式方法

1.2 找出基线条件，这种条件必须尽可能简单

1.3 不断将问题分解为简单问题，直到问题满足极基线条件

 

2. 算法计算时间

2.1 最好情况：

假设数组的长度为0~7这8个数字，且乱序排序，并且每次取正中间的值作为基线值 basevalue 。那么可结合二分查找的思想可知递归调用 logn +1 次，即树深为 logn+1 ，如下图所示：

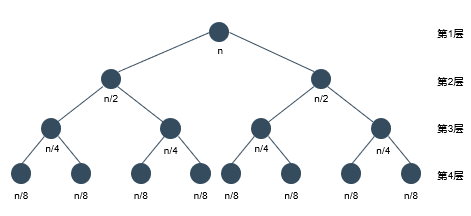
由于每次递归实际上都对n个元素进行了遍历判断，故算法复杂度为O(n*(logn +1)) = O(nlogn) 。

2.2 最糟情况：

数组升序排序，每次取第一个元素作为基线值 basevalue ，需要递归调用n次，每次递归实际上都对n个元素进行了遍历判断，故算法复杂度为O(n²) 。

2.3 平均情况：

最佳情况即平均情况，如果每次都随机选取数组中的一个元素作为基准值basevalue，那么快速排序的平均运行时间（算法复杂度）都为O(nlogn) 。

 

3. 快速排序的python实现

class solution(object):
    def quicksort(self, array):
        if len(array) < 2:
            return array
        basevalue = array[0]  # 基线条件
        left = [i for i in array[1:] if i <= basevalue]
        right = [j for j in array[1:] if j > basevalue]
        return self.quicksort(left) + [basevalue] + self.quicksort(right)  # 递归