NOIP2013 车站分级

NOIP2013 车站分级

题目描述

一条单向的铁路线上，依次有编号为1, 2, …, n的n个火车站。每个火车站都有一个级别，最低为1级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站x，则始发站、终点站之间所有级别大于等于火车站x的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）
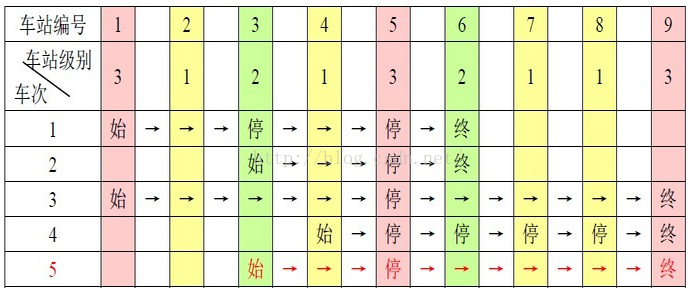
例如，下表是5趟车次的运行情况。其中，前4趟车次均满足要求，而第5趟车次由于停靠了3号火车站（2级）却未停靠途经的6号火车站（亦为2级）而不满足要求。

现有m趟车次的运行情况（全部满足要求），试推算这n个火车站至少分为几个不同的级别。

solution：

显然一辆车没有经过的站点的级别小于经过了的

由此可以把级别小的向级别大的连一条边表示小于的关系。

然后进行拓扑排序，在中途可以记录下当前的最大级别

注意：没有经过的站点是在起始站与终点站之间

#include<bits/stdc++.h>

using namespace std;

#define MAXN 1010

inline int read()
{
    int f=1,x=0;
    char ch;
    do
    {
        ch=getchar();
        if(ch=='-') f=-1;
    }while(ch<'0'||ch>'9');
    do
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }while(ch>='0'&&ch<='9');
    return f*x;
}

int n,m;
int a[MAXN][MAXN],s[MAXN];
bool g[MAXN][MAXN];
int top[MAXN];
int head[MAXN],cnt=0;
int in[MAXN];
bool vis[MAXN];
int ans=1;

inline void topsort()
{
    queue<pair<int,int> >q;
    for(int i=1;i<=n;i++)
    {
        if(!in[i]) q.push(make_pair(i,1));
    }
    while(q.size())
    {
        int u=q.front().first,v=q.front().second;
        q.pop();
        for(int i=1;i<=n;i++)
        {
            if(g[u][i]==1)
            {
                in[i]--;
                if(!in[i]) q.push(make_pair(i,v+1)),ans=max(ans,v+1);
            }
        }
    }
}

int main()
{
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    {
        memset(vis,0,sizeof(vis));
        s[i]=read();
        for(int j=1;j<=s[i];j++)
        {
            a[i][j]=read();
            vis[a[i][j]]=1;
        }
        for(int j=a[i][1];j<=a[i][s[i]];j++)
        {
            if(vis[j]) continue;
            else
            {
                for(int k=1;k<=s[i];k++)
                {
                    if(!g[j][a[i][k]])
                    {
                        g[j][a[i][k]]=1;
                        in[a[i][k]]++;
                        top[a[i][k]]++;
                    }
                }
            }
        }
    }
    topsort();
    printf("%d",ans);
}