1 Laplace算子的物理意义
Laplace算子的定义为梯度的散度。

在Cartesian坐标系下也可表示为:
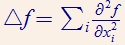
或者,它是Hessian矩阵的迹:

以热传导方程为例,因为热流与温度的梯度成正比,那么温度的梯度的散度就是热量的损失率。
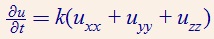
由此可见,Laplace算子可用于表现由于物质分布不均引起的物质输送。
2 Laplace算子的数学意义
现在,在一维空间中简单分析上面的式子:
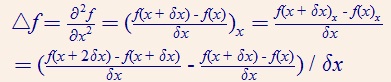
也可以写作:

把分子第一项和第二项分别按泰勒展开:
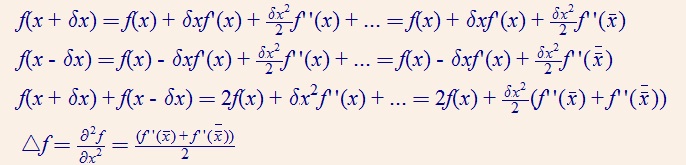
可以看出Laplace算子实际上是一个使函数取平均的算子。多维空间相似。
3 Laplace方程
若Laplace算子右边为零,称为Laplace方程。Laplace方程的解称为调和函数。若右边是一个函数,称为泊松方程。
4 Laplace算子在图像处理的运用
图像处理是以像素作为基础离散化,如下:
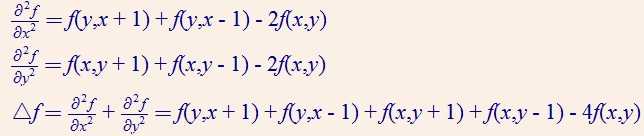
5 Laplacian 矩阵
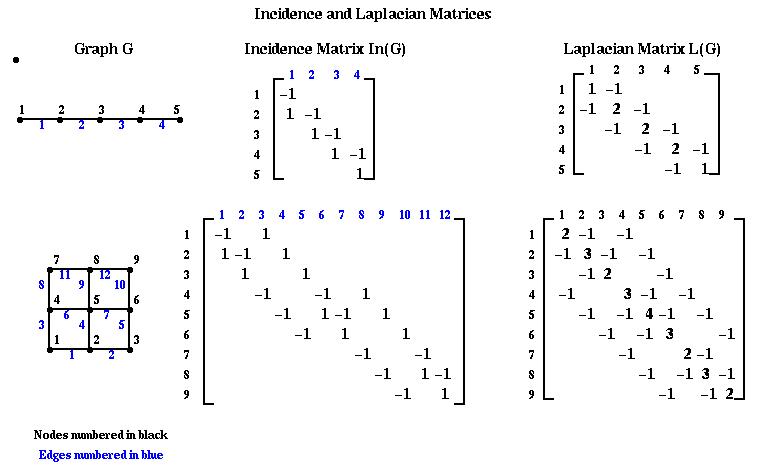
是一种用于表示图的矩阵。 它的维度是 |V|-by-|V| ( |V| 是节点的数目 )。 James Demmel提供了一种由Incidence matrix转化为Laplacian矩阵的方法。
In(G)是一个 |V|-by-|E| 矩阵( |E| 是边的数目 ), 设边e=(i,j),这一列除了第i行(为+1)和第j行(为-1)外都为零。 需要说明的是,根据这个定义,对于无向图 e=(i,j) 和 e=(j,i) 是等价的, 看似会生成很多不同的In图(根据每条边不同的取向)。但是实际上可以证明,无论边的方向怎么取,由In图生成的L图都是唯一的。 也就是说, e=(i,j) 和 e=(j,i) 怎么取是无关紧要的。 如何使用In图生成L图:
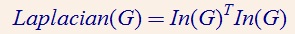
可得知Laplacian矩阵的两个重要性质:一是为对称阵。二是存在一个为零的特征值(秩为|V|-1)。三是一个半正定矩阵。 注意Laplace算子是负定的。
在求解含Laplacian矩阵的方程组时,常常要求为正定矩阵。观察发现这是因为Laplacian矩阵每列相加等于零。这时只需要手动更改第一行和第一列(比如第一个元素设为1,其余设为零),破坏其结构,令秩等于|V|就可以了。
对于非正定矩阵,左乘个transpose of the matrix, 推导如下:
Ax – b = 0
最小化 ||Ax – b||^2,展开后对x求导数:
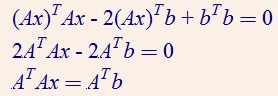
可转化为正定方程组。
6 Laplace算子和Laplacian矩阵的关系
Laplace算子可以推广到多维情况计算。Laplacian矩阵主要用于三维以下的图形学计算,可以表现复杂的几何结构。而Lapace方程使用了Laplace算子来表示Laplacian矩阵。