Tree

Tree：典型的数据结构属于一种阶层性非线性结，由一个或者一个之上节点组成有限集合，节点之间串联不会组成环，就叫树

度：子树个数该节点的度，包括从自己开始到其所在的叶子节点。在树种不是二叉树的树，树中

有些节点的子节点不一样的：为了极大化利用其存储空间，采用下列的存储格式，左边表示其子节点，右边表示其兄弟节点，儿子--兄弟表示方法，类似于二叉树结构。

二叉树：二叉树最多只能有2个节点的树，是一种典型的树结构不同于其他的树，度不超过2的树.

二叉树的性质：

*.第I层有做多2^(I-1)个节点

*。深度为K的二叉树的总节点（2^K）-1

*。叶子节点数N0，度为2节点数N2，度为1节点数N1： 总的边数：N0+N1+N2-1=0*N0+1*N1+2*N2

得出：N0=N2+1；

二叉树常被用于实现二叉查找树和二叉堆。

二叉排序树规则：大于父节点左右子树，左子树小于树根

1.满二叉树：树高度为，节点数2^H-1,节点编号按照从左到右从上到下的编号排序

2.完全二叉树：节点编号按照从左到右从上到下的编号排序，堆排序采用完全二叉树，堆采用完全二叉树，树按照大小排序。，中间没有阙短

每一次堆被打破之后对堆进行调整，堆排序

3.平衡二叉树AVL树：红黑树、AVL树、Treap等;

Problem:二叉排序树 Vs 堆

二叉排序树:左子树值比根节点小，右子树比根节点大，右子比左子树大，二叉排序树 为了动态的数据查找设计一种数据结构，在二叉排序树中查找一个结点的平均时间复杂度是O(log n)。

堆:父节点值大于（小于）子节点值，并没有规定左右节点值大小。为了排序设计一种数据结构，在堆中查找一个节点平均时间复杂度(o(n))

一。二叉树的遍历（按照由左往右方式）：按照树根的位置不同进行的命名，按照先左后右的结果

前序遍历：树根---左子树----右子树

中序遍历：左子树----树根---右子树，左--父--右---父的父节点

后序遍历：左子树----右子树---树根

最重要：Cout输出位置不同

中序遍历：从树根开始一直往左子树行走到底，遍历顺序一样从根到叶子节点，最重要的是调节输出顺序。

package BinaryTree;
//采用链表建立二叉排序树

public class binaryTree {
    public TreeNode rootNode;//二叉树的根节点
    //构造初始化
    public binaryTree(int [] data)
    {
        for(int i=0;i<data.length;i++)
        {
            Add_Node_to_Tree(data[i]);
        }
    }
    public void Add_Node_to_Tree(int value){
        //通过定义一个根节点对树进行记录
        TreeNode currentNode=rootNode;
        TreeNode tmp=new TreeNode(value);
        if(rootNode==null)
        {
            rootNode=new TreeNode(value);
            return;
        }
        //按照规则左子树值比根节点小，右子树比根节点大
        while(true)
        {
            //不断进行插入
            if(currentNode.value>value)
            {
                //没有堆这样的严格，只需要子节点与父节点局部符合要求，并不是AVL树或者堆，堆必须要整体要求
                //父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值,二叉树并没有这种要求
                if(currentNode.LeftNode==null)
                {
                    currentNode.LeftNode=tmp;
                    return;
                }else
                    currentNode=currentNode.LeftNode;
            }
            else
            {
                if(currentNode.RightNode==null)
                {
                    currentNode.RightNode=tmp;
                    return;
                }else
                    currentNode=currentNode.RightNode;
            }
            
        }
    }
    //前序遍历，递归调用顺序一样最重要的是输出的顺序不一样
    public void PreOrder(TreeNode node)
    {
        if(node!=null){
            //输出的结果
            System.out.print("["+node.value+"]");
            PreOrder(node.LeftNode);
            PreOrder(node.RightNode);
        }
    }
    //中序遍历
    public void InOrder(TreeNode node)
    {
        if(node!=null){
            //输出的结果
            
            InOrder(node.LeftNode);
            System.out.print("["+node.value+"]");
            InOrder(node.RightNode);
        }
    }
    public void PostOrder(TreeNode node)
    {
        if(node!=null){
            //输出的结果
            
            PostOrder(node.LeftNode);
            
            PostOrder(node.RightNode);
            System.out.print("["+node.value+"]");
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int []arr={7,4,1,5,16,8,11,12,15,9,2};
        int i;
        
        binaryTree Tree=new binaryTree(arr);
        
        System.out.println("前序遍历结果");
        Tree.PreOrder(Tree.rootNode);
        System.out.println();
        
        System.out.println("中序遍历结果");
        Tree.InOrder(Tree.rootNode);
        System.out.println();
        
        System.out.println("后序遍历结果");
        Tree.PostOrder(Tree.rootNode);
        System.out.println();
    }

}
class TreeNode{
    int value;
    TreeNode LeftNode;
    TreeNode RightNode;
    
    //构造函数
    public TreeNode(int value)
    {
        this.value=value;
        this.LeftNode=null;
        this.RightNode=null;
    }
}

前序遍历结果
[7][4][1][2][5][16][8][11][9][12][15]
中序遍历结果
[1][2][4][5][7][8][9][11][12][15][16]
后序遍历结果
[2][1][5][4][9][15][12][11][8][16][7]

 

 在C 语言中递归调用建立二叉树，此种递归的调用二叉树是前序遍历的方式：

函数参数传替方式：采用引用传递，其他传递：按值传递（对实参没有影响），指针传递（地址传递）会修改实参的值果在函数中反复利用指针进行间接访问，会使程序容易产生错误且难以阅读。

引用传递：，既可以使得对形参任何操作都能修改其相应的结构，同时调用方式自然。

#include<cstdio>
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
#define  ElementType char

//typedef struct TreeNode *BinTree;//为新的结构体TreeNode取新的名字BinTree
 typedef struct TreeNode {
    ElementType Data;

    struct TreeNode   *Left;
    struct TreeNode  * Right;
    //构造函数
}*BinTree,BinTNode ;
//建立二叉树有两种方式，一种建立struct，第二种采用的开辟一个内存，通过malloc看到其中指针变化
void CreateBinaryTree(BinTree &T)
{
    
    //终于把这种递归调用的形式理解了，此种方式将数据以前序遍历的方式进行
    //数据结构的递归存储，从树根一直往左到其左叶子节点，在从左叶子节点访问其右节点
    //明显的前序递归调用建立二叉树。
    
    char CH;
    cin>>CH;
    if (CH=='.')
        T=NULL;
    else
    {
        T=new BinTNode;
        ;

        T->Data=CH;
        CreateBinaryTree(T->Left);
        CreateBinaryTree(T->Right);
    }
}

void Pre_Order(BinTree &T){
//    cout<<"前序遍历"<<endl;
    //这里不能用指针
    if(T!=NULL){
        cout<<(T)->Data;
        Pre_Order((T)->Left);
        Pre_Order((T)->Right);
    }
}
//采用非递归的形式对数据进行中序遍历，Stack 
void Pre_Order_not(BinTree &T)
{//建立一个BinTree模板类型的堆栈
    stack<BinTree>S;
    

    //从树根一直遍历到左子树
    while(! S.empty()|| T)
    {
        while(T)
        {
            S.push(T);
            T=T->Left;
        }
        //S 中会保存其中的BinTree类型的堆栈
        if(!S.empty())
        {
            T=S.top();
            S.pop();
            cout<<T->Data;
            T=T->Right;
        }
    }
}
//层次遍历，使用队列进行
void Levelordertravel(BinTree &T)
{
    queue<BinTree>Q;
    if(!T) return;//空树返回
    Q.push(T);

    while(T && !Q.empty())
    {
        T=Q.front() ; 
    
        
        cout<<T->Data<<endl;
        if(T->Left) Q.push(T->Left);
        if (T->Right) Q.push(T->Right);
        Q.pop();
    }

}
int main()
{
    BinTree rootNode=new BinTNode;
    CreateBinaryTree( rootNode);
    //使用的是指针函数
    Pre_Order(rootNode);
    cout<<endl;
    BinTree tmp=rootNode;
    Pre_Order_not(rootNode);
    //使用的是引用递归在其中修改值会摆实参值进行修改
    cout<<endl;
    Levelordertravel(tmp);
    return 0;
}

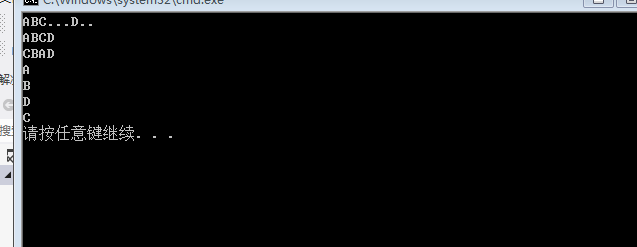
 采用递归先序遍历建立二叉树Java代码，Java中内存模型函数传递按值传递，栈内存存储的是对象在堆内存中地址

rootNode1节点通过断点调试可以看出最后可以用先序递归建立二叉树

package BinaryTree;
//采用链表建立二叉排序树

import java.io.IOException;
import java.util.Scanner;

public class binaryTree {
    public TreeNode rootNode;//二叉树的根节点
    //构造初始化
    public static TreeNode rootNode1;//递归调用建立一般二叉树
    public binaryTree(int [] data)
    {
        for(int i=0;i<data.length;i++)
        {
            Add_Node_to_Tree(data[i]);
        }
        System.out.println("递归调用建立二叉树");
        //这里递归建立二叉树运用的是用先序遍历方式建立二叉树，从树根到最左叶节点。
        rootNode1=REcord(rootNode1);
    }
    public static TreeNode REcord(TreeNode node)
    {
        
            int ch;
            Scanner sc=new Scanner(System.in);
            System.out.println("Enter a char");
             ch=sc.nextInt();
            System.out.println("read the char is:"+ch);
        
        
        if(ch==-1)
            { node=null;
                //return;
            }
        else
        {    
            node=new TreeNode(ch);
        node.LeftNode=REcord(node.LeftNode);
        node.RightNode=    REcord(node.RightNode);
        }
        
            return node;
    }
    
    public void Add_Node_to_Tree(int value){
        //通过定义一个根节点对树进行记录
        TreeNode currentNode=rootNode;
        TreeNode tmp=new TreeNode(value);
        if(rootNode==null)
        {
            rootNode=new TreeNode(value);
            return;
        }
        //按照规则左子树值比根节点小，右子树比根节点大
        while(true)
        {
            //不断进行插入
            if(currentNode.value>value)
            {
                //没有堆这样的严格，只需要子节点与父节点局部符合要求，并不是AVL树或者堆，堆必须要整体要求
                //父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值,二叉树并没有这种要求
                if(currentNode.LeftNode==null)
                {
                    currentNode.LeftNode=tmp;
                    return;
                }else
                    currentNode=currentNode.LeftNode;
            }
            else
            {
                if(currentNode.RightNode==null)
                {
                    currentNode.RightNode=tmp;
                    return;
                }else
                    currentNode=currentNode.RightNode;
            }
            
        }
    }
    //前序遍历，递归调用顺序一样最重要的是输出的顺序不一样
    public void PreOrder(TreeNode node)
    {
        if(node!=null){
            //输出的结果
            System.out.print("["+node.value+"]");
            PreOrder(node.LeftNode);
            PreOrder(node.RightNode);
        }
    }
    //中序遍历
    public void InOrder(TreeNode node)
    {
        if(node!=null){
            //输出的结果
            
            InOrder(node.LeftNode);
            System.out.print("["+node.value+"]");
            InOrder(node.RightNode);
        }
    }
    public void PostOrder(TreeNode node)
    {
        if(node!=null){
            //输出的结果
            
            PostOrder(node.LeftNode);
            
            PostOrder(node.RightNode);
            System.out.print("["+node.value+"]");
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int []arr={7,4,1,5,16,8,11,12,15,9,2};
        int i;
        
        binaryTree Tree=new binaryTree(arr);
        
        /*System.out.println("前序遍历结果");
        Tree.PreOrder(Tree.rootNode);
        System.out.println();
        
        System.out.println("中序遍历结果");
        Tree.InOrder(Tree.rootNode);
        System.out.println();
        
        System.out.println("后序遍历结果");
        Tree.PostOrder(Tree.rootNode);
        System.out.println();*/
    }

}
class TreeNode{
    int value;
    TreeNode LeftNode;
    TreeNode RightNode;
    
    //构造函数
    public TreeNode(int value)
    {
        this.value=value;
        this.LeftNode=null;
        this.RightNode=null;
    }
}

 采用泛型接口的方式递归构建二叉树：递归建立树的时候采用的是前序遍历的方式对树进行规则的输入。层次遍历过程中使用队列方式，一层层的进行遍历模拟

package Tree;

import java.util.Scanner;

//运用递归建立二叉树，递归采用前序遍历方式输入数据
public class BinaryTree<AnyType> {
@SuppressWarnings("rawtypes")
public static Node rootNode; 
    private static class Node<AnyType>
    {
        AnyType value;
        Node<AnyType>Left;
        Node<AnyType>Right;
        
        public Node(AnyType v)
        {
            this.value=v;
            this.Left=null;
            this.Right=null;
        }
    }
    
    public BinaryTree(AnyType []arr)
    {
        AnyType Val;
        
            //通过递归建立
            rootNode=AddNode(rootNode);
        //System.out.println(rootNode.value);
        PreOrder(rootNode);
    }
    public void PreOrder(Node P)
    {
        if(P!=null)
        {
            System.out.print("["+P.value+"]");
            PreOrder(P.Left);
            PreOrder(P.Right);
        }
    }
    private  Node <AnyType>AddNode(Node node)
    {
        int Val;
        @SuppressWarnings("resource")
        Scanner sc=new Scanner(System.in);
        System.out.println("Enter a char");
        Val=sc.nextInt();
        System.out.println("read the char is:"+Val);
        if((int)Val!=-1)
        {
            node=new Node<>(Val);
            node.Left=AddNode(node.Left);
            node.Right=AddNode(node.Right);
        }
        else
        {
            node=null;
        }
        return node;
        
        
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Integer [] Arr={7,4,1,5,16,8,11,12,15,9,2,-1};
        
        @SuppressWarnings("unused")
        BinaryTree <Integer>Tree=new BinaryTree<Integer>(Arr);
    }

}