前言:
太垃圾了
| [HNOI2006]公路修建问题 |
一开始看错题了草
意思是花费最多的一条公路尽量少,求最大花费的边
语文老师有教过最大的最小 最小的最大 就是二分
二分最多的那一条公路 然后看看第一公路够不够 反正不管总花费 所以全部选第一条 然后再选第二条 然后用并查集看看连不连通就好 sb题

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<set> #define Maxn 10010 using namespace std; struct node { int x,y,c; }; bool Cmp(const node &x,const node &y){return x.c<y.c;} node S1[Maxn*2],S2[Maxn*2]; int N,M,K; int fa[Maxn]; inline int find(int x){if(x==fa[x]) return x; else return fa[x]=find(fa[x]);} inline int FindS1(int x) { int L=1,R=M; int ret=-1; while(L<=R) { int mid=(L+R)>>1; if(S1[mid].c<=x){L=mid+1; ret=mid;} else R=mid-1; } return ret; } inline int FindS2(int x) { int L=1,R=M; int ret=-1; while(L<=R) { int mid=(L+R)>>1; if(S2[mid].c<=x){L=mid+1; ret=mid;} else R=mid-1; } return ret; } int main() { //freopen("a.in","r",stdin); //freopen("a.out","w",stdout); scanf("%d%d%d",&N,&K,&M); for(int i=1;i<M;i++) { int x,y,c1,c2; scanf("%d%d%d%d",&x,&y,&c1,&c2); node x1; x1.x=x; x1.y=y; x1.c=c1; node x2; x2.x=x; x2.y=y; x2.c=c2; S1[i]=x1; S2[i]=x2; } sort(S1+1,S1+M+1,Cmp); sort(S2+1,S2+M+1,Cmp); int L=1; int R=30000; int ret=-1; while(L<=R) { int mid=(L+R)>>1; int it1=FindS1(mid); int it2=FindS2(mid); int it; if(it1<K){L=mid+1; continue;} else if(it1+it2<N-1){L=mid+1; continue;} for(int i=1;i<=N;i++) fa[i]=i; int sum=0; for(it=1;it<=it1;it++) { int xx=find(S1[it].x); int yy=find(S1[it].y); if(xx!=yy){sum++; fa[xx]=yy;} } if(sum<K){L=mid+1; continue;} for(it=1;it<=it2;it++) { int xx=find(S2[it].x); int yy=find(S2[it].y); if(xx!=yy){sum++; fa[xx]=yy;} } if(sum==N-1){ret=mid; R=mid-1; continue;} else {L=mid+1; continue;} } printf("%d ",ret); return 0; } /* 10 4 20 3 9 6 3 1 3 4 1 5 3 10 2 8 9 8 7 6 8 8 3 7 1 3 2 4 9 9 5 10 8 9 1 2 6 9 1 6 7 9 8 2 6 2 1 3 8 9 5 3 2 9 6 1 6 10 3 5 6 3 1 2 7 6 1 7 8 6 2 10 9 2 1 7 1 10 2 */
| [Sdoi2011消耗战 |
虚树,题解的话我想做多几题再专门总结一下 其实虚树就是每个询问都建一棵树 这棵树包含的节点只是询问的节点和询问节点的lca,然后在新树上dp就好了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<vector> #include<climits> #define Maxn 250010 using namespace std; typedef long long LL; struct node{LL x,y,next,d;}edge[2][Maxn*2]; LL len[2],first[2][Maxn]; void ins(LL k,LL x,LL y,LL d){len[k]++; edge[k][len[k]].x=x; edge[k][len[k]].y=y; edge[k][len[k]].d=d; edge[k][len[k]].next=first[k][x]; first[k][x]=len[k];} LL dep[Maxn],fa[Maxn][21],minx[Maxn]; LL dfn[Maxn],id=0; LL N,M; void Dfs(LL x,LL f) { dfn[x]=++id; for(LL k=first[0][x];k!=-1;k=edge[0][k].next) { LL y=edge[0][k].y; if(y!=f){dep[y]=dep[x]+1; fa[y][0]=x; minx[y]=min(minx[x],edge[0][k].d); Dfs(y,x);} } } LL H[Maxn],K; LL top,S[Maxn]; bool Cmp(const LL &x,const LL &y){return dfn[x]<dfn[y];} LL lca(LL x,LL y) { if(dep[x]<dep[y]) swap(x,y); LL deep=dep[x]-dep[y]; for(LL i=20;i>=0;i--) if(deep>=(1<<i)){deep-=(1<<i); x=fa[x][i];} if(x==y) return x; for(LL i=20;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; } LL F[Maxn]; bool C[Maxn]; void DP(LL x) { F[x]=minx[x]; if(C[x]) return ; LL tmp=0; for(LL k=first[1][x];k!=-1;k=edge[1][k].next) { LL y=edge[1][k].y; DP(y); tmp+=F[y]; } if(tmp<F[x]) F[x]=tmp; } LL P[Maxn],Plen; void Solve() { for(LL i=1;i<=Plen;i++) first[1][P[i]]=-1; len[1]=0; scanf("%lld",&K); for(LL i=1;i<=K;i++) scanf("%lld",&H[i]),C[H[i]]=1; sort(H+1,H+K+1,Cmp); top=0; S[++top]=1; Plen=0; P[++Plen]=1; for(LL i=1;i<=K;i++) { LL now=H[i]; LL f=lca(S[top],now); while(dfn[S[top]]>dfn[f]){ins(1,S[top-1],S[top],0); top--;} if(dfn[S[top]]>dfn[f]){ins(1,f,S[top],0); top--;} if(S[top]!=f) S[++top]=f,P[++Plen]=f; if(S[top]!=now) S[++top]=now,P[++Plen]=now; } while(top>1){ins(1,S[top-1],S[top],0); top--;} DP(1); printf("%lld ",F[1]); for(LL i=1;i<=K;i++) C[H[i]]=0; } int main() { //freopen("a.in","r",stdin); //freopen("a.out","w",stdout); scanf("%lld",&N); len[0]=0; memset(first[0],-1,sizeof(first[0])); for(LL i=1;i<N;i++){LL x,y,d; scanf("%lld%lld%lld",&x,&y,&d); ins(0,x,y,d); ins(0,y,x,d);} dep[1]=1; for(LL i=1;i<=N;i++) minx[i]=LLONG_MAX; Dfs(1,0); for(LL j=1;j<=20;j++) for(LL i=1;i<=N;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; scanf("%lld",&M); len[1]=0; memset(first[1],-1,sizeof(first[1])); memset(C,0,sizeof(C)); for(LL i=1;i<=M;i++) Solve(); return 0; } /* 10 1 5 13 1 9 6 2 1 19 2 4 8 2 3 91 5 6 8 7 5 4 7 8 31 10 7 9 3 2 10 6 4 5 7 8 3 3 9 4 6 */
| [Hnoi2014]世界树 |
虚树,见 [DP优化方法之虚树]详谈

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<climits> #define Maxn 300010 using namespace std; const int inf=1e9; struct node { int x,y,next,d; }edge[2][Maxn*2]; int len[2],first[2][Maxn]; void ins(int k,int x,int y,int d){len[k]++; edge[k][len[k]].x=x; edge[k][len[k]].y=y; edge[k][len[k]].next=first[k][x]; first[k][x]=len[k];} int N,Q; int deep[Maxn],size[Maxn],fa[21][Maxn]; int dfn[Maxn],id=0; int unc[Maxn]; bool Cmp(const int &x,const int &y){return dfn[x]<dfn[y];} void Dfs(int x,int f) { size[x]=1; dfn[x]=++id; for(int k=first[0][x];k!=-1;k=edge[0][k].next) { int y=edge[0][k].y; if(y!=f) { deep[y]=deep[x]+1; fa[0][y]=x; Dfs(y,x); size[x]+=size[y]; } } } int lca(int x,int y) { if(deep[x]<deep[y]) swap(x,y); int d=(deep[x]-deep[y]); for(int i=20;i>=0;i--) if((1<<i)<=d) d-=(1<<i),x=fa[i][x]; if(x==y) return x; for(int i=20;i>=0;i--) if(fa[i][x]!=fa[i][y]) x=fa[i][x],y=fa[i][y]; return fa[0][x]; } int H[Maxn]; int P[Maxn],S[Maxn],top,plen; bool C[Maxn]; int dis(int x,int y){return deep[x]+deep[y]-2*deep[lca(x,y)];} pair<int,int> F1[Maxn],F2[Maxn],G[Maxn]; void Dfs1(int x) { if(C[x]) F1[x]=F2[x]=make_pair(0,x); for(int k=first[1][x];k!=-1;k=edge[1][k].next) { int y=edge[1][k].y; Dfs1(y); if(!C[x]) { int D=dis(x,y); if((F1[x].first>F1[y].first+D)||(F1[x].first==F1[y].first+D&&F1[x].second>F1[y].second)) F2[x]=F1[x],F1[x]=make_pair(F1[y].first+D,F1[y].second); else if((F2[x].first>F1[y].first+D)||(F2[x].first==F1[y].first+D&&F2[x].second>F1[y].second)) F2[x]=make_pair(F1[y].first+D,F1[y].second); } } } int F[Maxn]; void Dfs2(int x,int f) { if(!C[x]) { G[x].first=G[f].first+dis(x,f); G[x].second=G[f].second; if(F1[f].second==F1[x].second) { if((F2[f].first+dis(f,x)<G[x].first)||(F2[f].first+dis(f,x)==G[x].first&&F2[f].second<G[x].second)) G[x].second=F2[f].second,G[x].first=F2[f].first+dis(f,x); } else if((F1[f].first+dis(f,x)<G[x].first)||(F1[f].first+dis(f,x)==G[x].first&&F1[f].second<G[x].second)) G[x].second=F1[f].second,G[x].first=F1[f].first+dis(f,x); } else G[x]=make_pair(0,x); if(C[x]) F[x]=x; else { if(G[x].first<F1[x].first||(G[x].first==F1[x].first&&G[x].second<F1[x].second)) F[x]=G[x].second; if(G[x].first>F1[x].first||(G[x].first==F1[x].first&&G[x].second>F1[x].second)) F[x]=F1[x].second; } for(int k=first[1][x];k!=-1;k=edge[1][k].next) { int y=edge[1][k].y; Dfs2(y,x); } } int Find(int x,int D){for(int i=20;i>=0;i--) if(D>=(1<<i)) D-=(1<<i),x=fa[i][x]; return x;} int ans[Maxn]; void DP(int x) { ans[F[x]]++; unc[x]--; for(int k=first[1][x];k!=-1;k=edge[1][k].next) { int y=edge[1][k].y; int L=Find(y,deep[y]-deep[x]-1); int R=fa[0][y]; int sizex=size[L]; unc[x]-=sizex; int ret=x; if(F[x]!=F[y]) { if(deep[L]<=deep[R]) { while(deep[L]<=deep[R]) { int mid=(deep[L]+deep[R])>>1; int midx=Find(y,deep[y]-mid); int disx=dis(F[x],midx); int disy=dis(F[y],midx); if(disx>disy||(disx==disy&&F[x]>F[y])) R=Find(y,deep[y]-(mid-1)); else if(disx<disy||(disx==disy&&F[x]<F[y])) L=Find(y,deep[y]-(mid+1)),ret=midx; } ans[F[x]]+=size[Find(y,deep[y]-deep[x]-1)]-size[Find(y,deep[y]-deep[ret]-1)]; ans[F[y]]+=size[Find(y,deep[y]-deep[ret]-1)]-size[y]; } } else ans[F[x]]+=size[Find(y,deep[y]-deep[x]-1)]-size[y]; } for(int k=first[1][x];k!=-1;k=edge[1][k].next) { int y=edge[1][k].y; DP(y); } } int B[Maxn]; void Solve() { int K; scanf("%d",&K); for(int i=1;i<=K;i++){scanf("%d",&H[i]); B[i]=H[i]; C[H[i]]=1;} sort(H+1,H+K+1,Cmp); top=1; S[top]=1; plen=1; P[1]=1; for(int i=1;i<=K;i++) { int now=H[i]; int f=lca(now,S[top]); while(dfn[S[top-1]]>dfn[f]) ins(1,S[top-1],S[top],0),top--; if(dfn[S[top]]>dfn[f]) ins(1,f,S[top],0),top--; if(S[top]!=f) S[++top]=f,P[++plen]=f; if(S[top]!=now) S[++top]=now,P[++plen]=now; } while(top>1) ins(1,S[top-1],S[top],0),top--; Dfs1(1); Dfs2(1,0); for(int i=1;i<=plen;i++) unc[P[i]]=size[P[i]]; DP(1); for(int i=1;i<=plen;i++) ans[F[P[i]]]+=unc[P[i]]; for(int i=1;i<=K;i++) printf("%d ",ans[B[i]]); printf(" "); for(int i=1;i<=K;i++) ans[H[i]]=0; for(int i=1;i<=K;i++) C[H[i]]=0; for(int i=1;i<=plen;i++) F1[P[i]].first=F1[P[i]].second=F2[P[i]].first=F2[P[i]].second=G[P[i]].first=G[P[i]].second=F[P[i]]=inf,first[1][P[i]]=-1; len[1]=0; } int main() { scanf("%d",&N); len[0]=0; memset(first[0],-1,sizeof(first[0])); for(int i=1;i<N;i++){int x,y; scanf("%d%d",&x,&y); ins(0,x,y,1); ins(0,y,x,1);} Dfs(1,0); for(int i=1;i<=20;i++) for(int j=1;j<=N;j++) fa[i][j]=fa[i-1][fa[i-1][j]]; memset(first[1],-1,sizeof(first[1])); len[1]=0; for(int i=0;i<=N;i++) F1[i].first=F1[i].second=F2[i].first=F2[i].second=G[i].first=G[i].second=F[i]=inf; for(int i=1;i<=N;i++) ans[i]=0; scanf("%d",&Q); for(int i=1;i<=Q;i++) Solve(); return 0; } /* 10 2 1 3 2 4 3 5 4 6 1 7 3 8 3 9 4 10 1 5 2 6 1 5 2 7 3 6 9 1 8 4 8 7 10 3 5 2 9 3 5 8 */
| [HNOI2006]鬼谷子的钱袋 |
结论题 从小拿起 差不多二进制这样子

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> using namespace std; int main() { int N; scanf("%d",&N); int sum=0; for(int i=0;;i++) if(N>=(1<<i)) sum++,N-=(1<<i); else break; return printf("%d ",(N>0)?(sum+1):sum),0; }
| [HNOI2006]超级英雄Hero |
匈牙利裸题

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; const int Maxn=1010; struct node { int x,y,next; }edge[Maxn*2]; int len,first[Maxn*2]; void ins(int x,int y){len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len;} int N,M; bool chw[Maxn]; int match[Maxn]; bool Find(int x) { for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(!chw[y]) { chw[y]=1; if(match[y]==0||Find(match[y])){match[y]=x; return 1;} } } return 0; } int main() { scanf("%d%d",&N,&M); len=0; memset(first,-1,sizeof(first)); for(int i=1;i<=M;i++) { int x,y; scanf("%d%d",&x,&y); ins(i,x); ins(i,y); } for(int i=1;i<=N;i++) { memset(chw,0,sizeof(chw)); if(!Find(i)){printf("%d ",i-1); return 0;} } return printf("%d ",N),0; }
| [Apio2009]Atm |
SPFA+Tarjan缩点

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<stack> #include<queue> using namespace std; const int Maxn=500010; pair<int,int>pr[Maxn]; struct node { int x,y,next; }edge[Maxn]; int len,first[Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } int N,M; int Val[Maxn]; int low[Maxn],dfn[Maxn],belong[Maxn],cnt,id,tp; stack<int>S; bool insta[Maxn]; void dfs(int x) { dfn[x]=low[x]=++id; S.push(x); insta[x]=1; for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(dfn[y]==-1){dfs(y); low[x]=min(low[x],low[y]);} else if(insta[y]) low[x]=min(low[x],dfn[y]); } if(dfn[x]==low[x]) { int i; cnt++; do { i=S.top(); belong[i]=cnt; insta[i]=false; S.pop(); }while(i!=x); } } int ST,P; int sum[Maxn]; bool V[Maxn]; int D[Maxn]; queue<int>Q; void Spfa() { memset(V,0,sizeof(V)); V[belong[ST]]=1; memset(D,0,sizeof(D)); D[belong[ST]]=sum[belong[ST]]; Q.push(belong[ST]); while(!Q.empty()) { int x=Q.front(); for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(D[y]<D[x]+sum[y]) { D[y]=D[x]+sum[y]; if(!V[y]) V[y]=true,Q.push(y); } } V[x]=false; Q.pop(); } } int main() { scanf("%d%d",&N,&M); memset(first,-1,sizeof(first)); for(int i=1;i<=M;i++) { scanf("%d%d",&pr[i].first,&pr[i].second); ins(pr[i].first,pr[i].second); } memset(insta,0,sizeof(insta)); memset(low,-1,sizeof(low)); memset(dfn,-1,sizeof(dfn)); for(int i=1;i<=N;i++) { if(dfn[i]==-1) dfs(i); } for(int i=1;i<=N;i++) scanf("%d",&Val[i]); for(int i=1;i<=N;i++) sum[belong[i]]+=Val[i]; scanf("%d%d",&ST,&P); len=0; memset(first,-1,sizeof(first)); for(int i=1;i<=M;i++) { if(belong[pr[i].first]!=belong[pr[i].second]) ins(belong[pr[i].first],belong[pr[i].second]); } Spfa(); int maxx=0; for(int i=1;i<=P;i++) { int x; scanf("%d",&x); maxx=max(maxx,D[belong[x]]); } return printf("%d ",maxx),0; } /* 6 7 1 2 2 3 3 5 2 4 4 1 2 6 6 5 10 12 8 16 1 5 1 4 4 3 5 6 */
| [CTSC2008]祭祀river |
最长反链覆盖=最小路径覆盖=N-最大匹配数 Floyd好了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> using namespace std; const int Maxn=110; struct node { int x,y,next; }edge[Maxn*Maxn]; int len,first[Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } int match[Maxn]; bool chw[Maxn]; int N,M; int F[Maxn][Maxn]; bool Find(int x) { for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(chw[y]==0) { chw[y]=1; if(match[y]==0||Find(match[y])){match[y]=x; return 1;} } } return 0; } void Match() { int ans=0; memset(match,0,sizeof(match)); for(int i=1;i<=N;i++) { memset(chw,0,sizeof(chw)); if(Find(i)) ans++; } printf("%d ",N-ans); } int main() { scanf("%d%d",&N,&M); len=0; memset(first,-1,sizeof(first)); memset(F,63,sizeof(F)); for(int i=1;i<=M;i++) { int x,y; scanf("%d%d",&x,&y); F[x][y]=0; } for(int k=1;k<=N;k++) for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) F[i][j]=min(F[i][k]+F[k][j],F[i][j]); for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) if(F[i][j]<99999999) ins(i,j); Match(); return 0; }
| [Hnoi2013]游走 |
很好的题 最后问了李奥
首先对于无向图来说 总的期望就是每条边经过的期望乘于权值
试想图确定了 每条边经过的期望也是确定的
但是直接算不好求
然后就用点的期望推出边的期望 就等于两端的点走过来这一条边
点的期望怎么做呢 无向图的话 可以走过去又走回来 (当然有向有环图也得这么做)
那么我们考虑列出方程 用高斯消元做
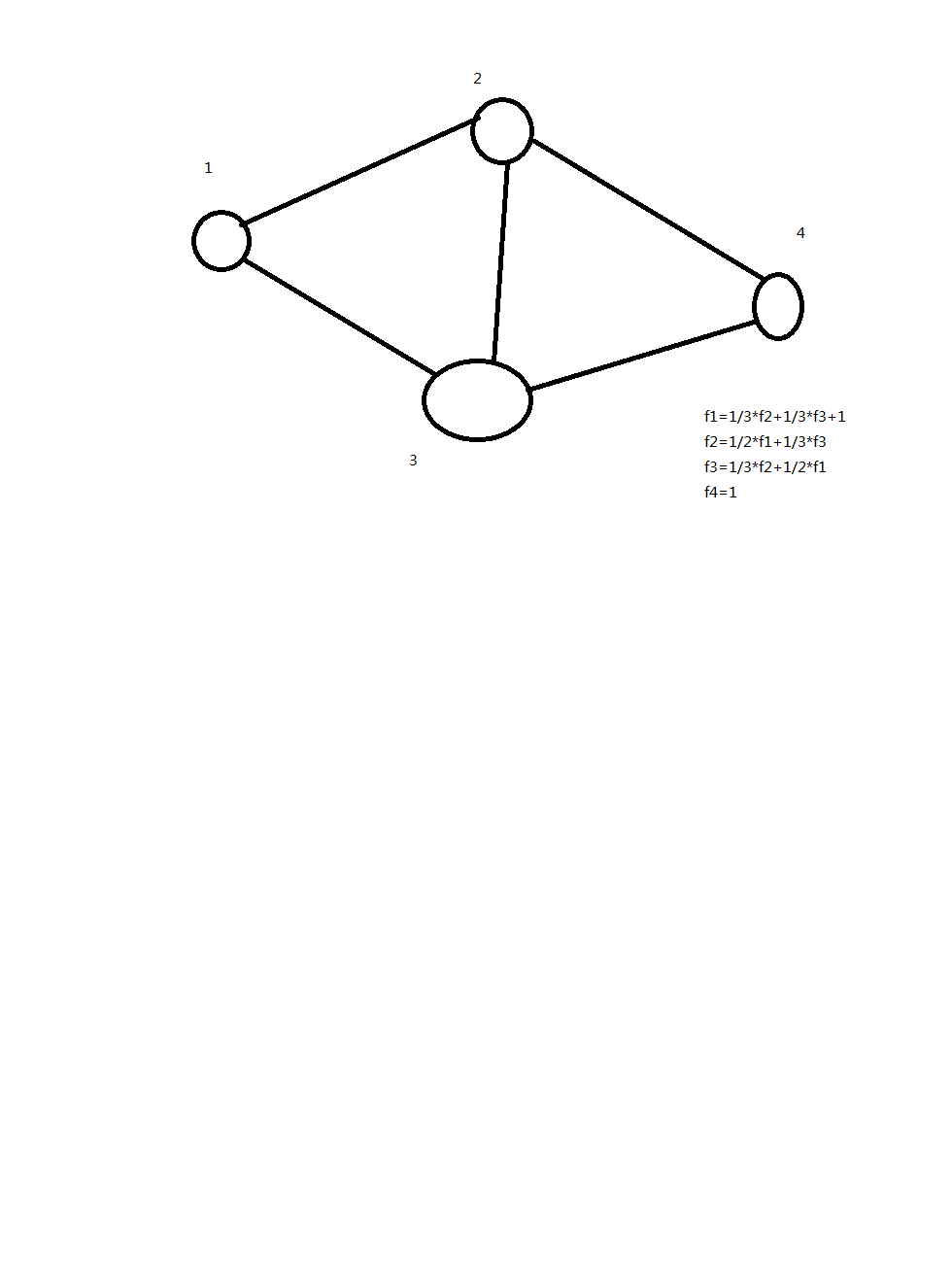
F1要加1 因为从它开始的 Fn=1 显然嘛 终点的期望都是1
连边考虑从哪里来 有多少概率来连边 加起来就是期望
然后解出来就完事了 卡精度用long double 我不会输出 然后强制转double输出 :)

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<vector> using namespace std; const long double EPS=1e-12; const int Maxn=510; int N,M; pair<int,int>pr[Maxn*Maxn]; long double ru[Maxn]; long double A[Maxn][Maxn]; vector<int>Vec[Maxn]; long double F[Maxn]; void Gauss() { for(int i=1;i<=N;i++) { for(int j=i;j<=N;j++) { if(fabs(A[j][i])>EPS) { for(int k=i;k<=N+1;k++) swap(A[i][k],A[j][k]); break; } } for(int j=i+1;j<=N;j++) { if(fabs(A[j][i])>EPS) { long double K=A[i][i]/A[j][i]; for(int k=i;k<=N+1;k++) A[j][k]=A[i][k]-A[j][k]*K; } } } for(int i=N;i>=1;i--) { long double s=A[i][N+1]; for(int j=N;j>i;j--) s-=F[j]*A[i][j]; F[i]=s/A[i][i]; } } long double D[Maxn*Maxn]; int main() { scanf("%d%d",&N,&M); for(int i=1;i<=M;i++) { scanf("%d%d",&pr[i].first,&pr[i].second); ru[pr[i].second]++; ru[pr[i].first]++; if(pr[i].first!=N) Vec[pr[i].second].push_back(pr[i].first); if(pr[i].second!=N) Vec[pr[i].first].push_back(pr[i].second); } for(int i=1;i<N;i++) { if(i==1) A[i][N+1]=-1.0; A[i][i]=-1.0; for(int j=0;j<Vec[i].size();j++) A[i][Vec[i][j]]=1.0/ru[Vec[i][j]]; }A[N][N]=1.0; A[N][N+1]=1.0; Gauss(); long double ans=0.0; for(int i=1;i<=M;i++) { if(pr[i].first!=N) D[i]+=F[pr[i].first]*(1/ru[pr[i].first]); if(pr[i].second!=N) D[i]+=F[pr[i].second]*(1/ru[pr[i].second]); } sort(D+1,D+M+1); for(int i=1;i<=M;i++) ans+=D[i]*(M-i+1); return printf("%.3lf ",(double)ans),0; } /* 3 3 2 3 1 2 1 3 */
| [HAOI2012]高速公路(road) |
线段树好题 很容易得知每条路的价值为sigma( (i-l+1)*(r-i)*v[i] )
展开之后 维护三个值就好了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<ctime> using namespace std; typedef long long LL; const LL Maxn=100010; LL N,M; LL root,lc[Maxn*4],rc[Maxn*4]; LL C[Maxn*4],C1[Maxn*4],C2[Maxn*4]; LL tot; LL lazy[Maxn*4]; LL S1[Maxn*4],S2[Maxn*4]; void Push_down(LL u,LL L,LL R) { if(lazy[u]) { LL mid=(L+R)>>1; C[lc[u]]+=lazy[u]*(mid-L+1); C[rc[u]]+=lazy[u]*(R-mid); C1[lc[u]]+=lazy[u]*(S1[mid]-S1[L-1]); C1[rc[u]]+=lazy[u]*(S1[R]-S1[mid]); C2[lc[u]]+=lazy[u]*(S2[mid]-S2[L-1]); C2[rc[u]]+=lazy[u]*(S2[R]-S2[mid]); lazy[lc[u]]+=lazy[u]; lazy[rc[u]]+=lazy[u]; lazy[u]=0; } } void Link(LL &u,LL L,LL R,LL l,LL r,LL c) { if(!u) u=++tot; if(L==l&&R==r){C[u]+=c*(R-L+1); C1[u]+=c*(S1[r]-S1[l-1]); C2[u]+=c*(S2[r]-S2[l-1]); lazy[u]+=c; return ;} Push_down(u,L,R); LL mid=(L+R)>>1; if(r<=mid) Link(lc[u],L,mid,l,r,c); else if(l>mid) Link(rc[u],mid+1,R,l,r,c); else { Link(lc[u],L,mid,l,mid,c); Link(rc[u],mid+1,R,mid+1,r,c); } C[u]=C[lc[u]]+C[rc[u]]; C1[u]=C1[lc[u]]+C1[rc[u]]; C2[u]=C2[lc[u]]+C2[rc[u]]; } LL c,c1,c2; void Query(LL u,LL L,LL R,LL l,LL r) { if(!u) return ; if(L==l&&R==r){c+=C[u]; c1+=C1[u]; c2+=C2[u]; return ;} Push_down(u,L,R); LL mid=(L+R)>>1; if(r<=mid) Query(lc[u],L,mid,l,r); else if(l>mid) Query(rc[u],mid+1,R,l,r); else { Query(lc[u],L,mid,l,mid); Query(rc[u],mid+1,R,mid+1,r); } } LL gcd(LL x,LL y){if(y==0) return x; else return gcd(y,x%y);} LL py[Maxn]; int main() { scanf("%lld%lld",&N,&M); tot=0; for(LL i=1;i<=N;i++) S1[i]=S1[i-1]+i,S2[i]=S2[i-1]+i*i; py[2]=1; for(LL i=3;i<=N;i++) py[i]=py[i-1]+(i-1); for(LL i=1;i<=N;i++) Link(root,1,N,i,i,0); for(LL i=1;i<=M;i++) { char st; scanf(" %c",&st); if(st=='C') { LL L,R,D; scanf("%lld%lld%lld",&L,&R,&D); R--; Link(root,1,N,L,R,D); } else { LL L,R; scanf("%lld%lld",&L,&R); c=c1=c2=0; Query(root,1,N,L,R-1); LL px=(R-(R*L))*c+(R+L-1)*c1-c2; LL g=gcd(px,py[R-L+1]); printf("%lld/%lld ",px/g,py[R-L+1]/g); } } return 0; } /* 4 5 C 1 4 2 C 1 2 -1 Q 1 2 Q 2 4 Q 1 4 */
| [SCOI2012]奇怪的游戏 |
感觉是高斯消元 看了看数据范围 又看了看是密集的图 所以感觉是网络流 但是流量不能等分...
膜题解
首先黑白染色 0为黑 1为白 num为个数 val为总和
我们考虑发现一条等式 num[0]*x-val[0]=num[1]*x-val[1] x是所有的数将要达到的数
解得x的话就直接网络流check
x为增根的话 就考虑二分 想一想 当且仅当 num[0]=num[1]时才出现 那么这个肯定具有二分性
假定k为最小的 对于任意x>=k 一定合法 也就是把整个图再覆盖一遍 黑白相等重新覆盖一遍没有问题
之后应该怎么网络流呢...
流量不能等分 但可以从一边到另一边
(ST,Black_Point,x-V) (Black_Point,White_Point,inf) (Black_Point,White_Point,x-V)
满流即可

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> using namespace std; typedef long long LL; const LL Maxn=110; const LL inf=1e12+7; struct node { LL x,y,next,c,other; }edge[Maxn*Maxn*2]; LL len,first[Maxn*Maxn]; void ins(LL x,LL y,LL c) { len++; LL k1=len; edge[len].x=x; edge[len].y=y; edge[len].c=c; edge[len].next=first[x]; first[x]=len; len++; LL k2=len; edge[len].x=y; edge[len].y=x; edge[len].c=0; edge[len].next=first[y]; first[y]=len; edge[k1].other=k2; edge[k2].other=k1; } LL T,N,M; LL Val[Maxn][Maxn]; bool bw[Maxn][Maxn]; LL pw,pb,sw,sb; LL ST,ED; LL dx[Maxn]={-1,0,1,0}; LL dy[Maxn]={0,1,0,-1}; LL dep[Maxn*Maxn]; queue<LL>Q; bool Bfs() { while(!Q.empty()) Q.pop(); Q.push(ST); memset(dep,0,sizeof(dep)); dep[ST]=1; while(!Q.empty()) { LL x=Q.front(); for(LL k=first[x];k!=-1;k=edge[k].next) { LL y=edge[k].y; if(dep[y]==0&&edge[k].c) { dep[y]=dep[x]+1; Q.push(y); } } Q.pop(); } return dep[ED]>0; } LL Dfs(LL x,LL Flow) { if(x==ED) return Flow; LL delta=0; for(LL k=first[x];k!=-1;k=edge[k].next) { LL y=edge[k].y; if(edge[k].c&&dep[y]==dep[x]+1&&Flow>delta) { LL minf=Dfs(y,min(Flow-delta,edge[k].c)); delta+=minf; edge[k].c-=minf; edge[edge[k].other].c+=minf; } } if(delta==0) dep[x]=0; return delta; } bool Check(LL d) { ST=N*M+1; ED=N*M+2; len=0; memset(first,-1,sizeof(first)); for(LL i=1;i<=N;i++) { for(LL j=1;j<=M;j++) { if(bw[i][j]==0) { for(LL k=0;k<4;k++) { LL xx=i+dx[k]; LL yy=j+dy[k]; if(xx<=N&&xx>0&&yy<=M&&yy>0) ins((i-1)*M+j,(xx-1)*M+yy,inf); } } } } for(LL i=1;i<=N;i++) for(LL j=1;j<=M;j++) { if(!bw[i][j]) ins(ST,(i-1)*M+j,d-Val[i][j]); else ins((i-1)*M+j,ED,d-Val[i][j]); } LL ans=0,delta; while(Bfs()) { if(delta=Dfs(ST,inf)) ans+=delta; } if(ans==pb*d-sb) return 1; return 0; } int main() { scanf("%lld",&T); while(T--) { scanf("%lld%lld",&N,&M); memset(bw,0,sizeof(bw)); LL maxx=0; for(LL i=1;i<=N;i++) for(LL j=1;j<=M;j++) scanf("%lld",&Val[i][j]),maxx=max(maxx,Val[i][j]); pw=0,pb=0,sw=0,sb=0; bw[0][1]=1; for(LL i=1;i<=N;i++) { bw[i][1]=bw[i-1][1]^1; if(bw[i][1]) pw++,sw+=Val[i][1]; else pb++,sb+=Val[i][1]; for(LL j=2;j<=M;j++) { bw[i][j]=bw[i][j-1]^1; if(bw[i][j]) pw++,sw+=Val[i][j]; else pb++,sb+=Val[i][j]; } } if(pw!=pb) { LL x=(sb-sw)/(pb-pw); if(x<maxx){printf("-1 "); continue;} if(Check(x)) printf("%lld ",pb*x-sb); else printf("-1 "); } else { if(pb==pw&&sb!=sw){printf("-1 "); continue;} LL L=maxx; LL R=inf; LL ret=-1; while(L<=R) { LL mid=(L+R)>>1; if(Check(mid)) R=mid-1,ret=mid; else L=mid+1; } printf("%lld ",pb*ret-sb); } } return 0; }
| [SCOI2012]滑雪与时间胶囊 |
好题 一开始以为很水 首先是最小有根树 然后考虑特殊性质 点都是从高到低的
Kursal不能做有根树是因为把你逆向的边都合起来了 而在这题中 正向的边都是从高到低的

这是不正确决策的图 那么为了正确决策 我们应该把终点高度高到低排一下
这样就可以了 为什么呢 我肯定想不到
顺着高度下来的一定合法 你看这种情况 8一定先连到6 再连到5 这样6就连不到5了 其实也是避免了6没有入度 只有出度
意会一下就好了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Maxn=1000010; struct node { LL x,y,d,next; }edge[Maxn*2]; LL len,first[Maxn]; void ins(LL x,LL y,LL d) { len++; edge[len].x=x; edge[len].y=y; edge[len].d=d; edge[len].next=first[x]; first[x]=len; } LL N,M; LL H[Maxn]; LL D[Maxn]; bool vis[Maxn]; LL ans=0,maxx=0; void Dfs(LL x) { vis[x]=1; maxx++; for(LL k=first[x];k!=-1;k=edge[k].next) { LL y=edge[k].y; if(!vis[y]) Dfs(y); } } bool Cmp(const node &x,const node &y){if(H[x.y]!=H[y.y]) return H[x.y]>H[y.y]; return x.d<y.d;} LL fa[Maxn]; LL Find(LL x){if(x==fa[x]) return x; else return fa[x]=Find(fa[x]);} int main() { scanf("%lld%lld",&N,&M); len=0; memset(first,-1,sizeof(first)); for(LL i=1;i<=N;i++) scanf("%lld",&H[i]); for(LL i=1;i<=M;i++) { LL x,y,d; scanf("%lld%lld%lld",&x,&y,&d); if(H[x]>=H[y]) ins(x,y,d); if(H[y]>=H[x]) ins(y,x,d); } memset(D,63,sizeof(D)); D[1]=0; memset(vis,0,sizeof(vis)); vis[1]=1; Dfs(1); sort(edge+1,edge+len+1,Cmp); for(LL i=1;i<=N;i++) fa[i]=i; for(LL i=1;i<=len;i++) { if(!vis[edge[i].x]||!vis[edge[i].y]) continue; LL xx=Find(edge[i].x); LL yy=Find(edge[i].y); if(xx!=yy) { fa[xx]=yy; ans+=edge[i].d; } } return printf("%lld %lld ",maxx,ans),0; } /* 3 3 3 2 1 1 2 1 2 3 1 1 3 10 */
| [JLOI2012]树 |
ST表水题

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=100010; int N,M,S; int dis[Maxn][30]; int fa[Maxn][30]; int Val[Maxn]; int main() { scanf("%d%d",&N,&S); for(int i=1;i<=N;i++) scanf("%d",&Val[i]); memset(fa,-1,sizeof(fa)); fa[1][0]=0; dis[1][0]=Val[1]; for(int i=1;i<N;i++) { int x,y; scanf("%d%d",&x,&y); fa[y][0]=x; dis[y][0]=Val[y]; } for(int j=1;j<=20;j++) for(int i=1;i<=N;i++) fa[i][j]=fa[fa[i][j-1]][j-1],dis[i][j]=dis[fa[i][j-1]][j-1]+dis[i][j-1]; int ans=0; for(int i=1;i<=N;i++) { int s=S; int x=i; for(int j=20;j>=0;j--) if((fa[x][j]!=-1)&&(dis[x][j]<=s)) s-=dis[x][j],x=fa[x][j]; if(s==0) ans++; } return printf("%d ",ans),0; }
| [SCOI2012]喵星球上的点名 |
恶心的ac自动机 字典树用map和vector 导致自动机不能直接建虚节点做 然后码了很久
最后暴力跳fail 其实建fail树 然后搜下去找子串 再用hash或者map去去重即可
(时间复杂度算是过不了的 数据水)

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<map> #include<queue> #include<vector> using namespace std; const int Maxn=500000; struct node { int d,fail,w; map<int,int>mp; vector<int>Child,next; vector<int>num; }tr[Maxn]; int tot,rot=0; int T=0; void Tnew(int u) { tr[u].mp.clear(); tr[u].num.clear(); tr[u].d=-1; tr[u].fail=tr[u].w=0; tr[u].Child.clear(); tr[u].num.clear(); } int A[Maxn*2]; int last[Maxn]; void Build(int L) { int u=rot; for(int i=1;i<=L;i++) { int x=A[i]; if(tr[u].mp[x]==0) { tr[u].mp[x]=++tr[u].w; Tnew(++tot); tr[tot].d=x; tr[u].Child.push_back(tot); tr[u].next.push_back(tot); u=tot; tr[u].num.push_back(T); } else{u=tr[u].Child[tr[u].mp[x]-1]; tr[u].num.push_back(T);} } last[T]=u; } queue<int>Q; void AC_Tire() { while(!Q.empty()) Q.pop(); Q.push(rot); while(!Q.empty()) { int u=Q.front(); for(int i=0;i<tr[u].Child.size();i++) { int uu=tr[u].fail; int j=tr[u].Child[i]; if(u==0) tr[tr[u].Child[i]].fail=0; else { while(uu!=0&&tr[uu].mp[tr[j].d]==0) uu=tr[uu].fail; if(tr[uu].mp[tr[j].d]==0) tr[j].fail=0; else tr[j].fail=tr[uu].Child[tr[uu].mp[tr[j].d]-1]; } Q.push(tr[u].Child[i]); } Q.pop(); } } int N,M; struct E { int x,y,next; }edge[Maxn]; int len,first[Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } int ansA[Maxn],ansB[Maxn]; map<int,bool>mp; void Dfs(int root,int x) { for(int i=0;i<tr[x].num.size();i++) { int j=tr[x].num[i]; if(j<=N) { if(mp[j]==0) { mp[j]=1; ansA[root]++; ansB[j]++; } } } for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; Dfs(root,y); } } int main() { scanf("%d%d",&N,&M); Tnew(0); tot=rot=0; for(int i=1;i<=N;i++) { int L1,L2; scanf("%d",&L1); T++; for(int j=1;j<=L1;j++) scanf("%d",&A[j]); A[L1+1]=10001; scanf("%d",&L2); for(int j=1;j<=L2;j++) scanf("%d",&A[L1+1+j]); Build(L1+L2+1); } for(int i=1;i<=M;i++) { int L; scanf("%d",&L); T++; for(int j=1;j<=L;j++) scanf("%d",&A[j]); Build(L); } AC_Tire(); len=0; memset(first,-1,sizeof(first)); for(int i=2;i<=tot;i++) ins(tr[i].fail,i); for(int i=N+1;i<=N+M;i++) { mp.clear(); Dfs(i-N,last[i]); } for(int i=1;i<=M;i++) printf("%d ",ansA[i]); for(int i=1;i<N;i++) printf("%d ",ansB[i]); printf("%d ",ansB[N]); return 0; } /* 2 3 6 8 25 0 24 14 8 6 18 0 10 20 24 0 7 14 17 8 7 0 17 0 5 8 25 0 24 0 4 8 25 0 24 4 7 0 17 0 4 17 0 8 25 */
| [POI2007]大都市meg |
sb树剖

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=250010; struct node { int x,y,d,next; }edge[Maxn*2]; int len,first[Maxn]; void ins(int x,int y,int d) { len++; edge[len].x=x; edge[len].y=y; edge[len].d=d; edge[len].next=first[x]; first[x]=len; } int N; int dep[Maxn],fa[Maxn]; int son[Maxn],size[Maxn]; void Dfs(int x) { size[x]=1; son[x]=0; for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(dep[y]==0) { dep[y]=dep[x]+1; fa[y]=x; Dfs(y); if(size[son[x]]<size[y]) son[x]=y; size[x]+=size[y]; } } } int top[Maxn],w[Maxn],z; void Dfs1(int x,int tp) { top[x]=tp; w[x]=++z; if(son[x]) Dfs1(son[x],tp); for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(y!=son[x]&&y!=fa[x]) Dfs1(y,y); } } int root,tot,lc[Maxn*4],rc[Maxn*4],C[Maxn*4]; void Link(int &u,int L,int R,int k,int c) { if(!u) u=++tot; if(L==R){C[u]=c; return ;} int mid=(L+R)>>1; if(k<=mid) Link(lc[u],L,mid,k,c); else Link(rc[u],mid+1,R,k,c); C[u]=C[lc[u]]+C[rc[u]]; } void Change(int u,int L,int R,int k,int c) { if(L==R){C[u]=c; return ;} int mid=(L+R)>>1; if(k<=mid) Change(lc[u],L,mid,k,c); else Change(rc[u],mid+1,R,k,c); C[u]=C[lc[u]]+C[rc[u]]; } int Query(int u,int L,int R,int l,int r) { if(L==l&&R==r) return C[u]; int mid=(L+R)>>1; if(r<=mid) return Query(lc[u],L,mid,l,r); else if(l>mid) return Query(rc[u],mid+1,R,l,r); else { return Query(lc[u],L,mid,l,mid)+Query(rc[u],mid+1,R,mid+1,r); } } void C_(int x,int y) { if(dep[x]<dep[y]) swap(x,y); Change(root,1,z,w[x],0); } int Q(int x,int y) { int ans=0; int tx=top[x]; int ty=top[y]; while(tx!=ty) { if(dep[tx]<dep[ty]) swap(tx,ty),swap(x,y); ans+=Query(root,1,z,w[tx],w[x]); x=fa[tx]; tx=top[x]; } if(x==y) return ans; if(dep[x]<dep[y]) swap(x,y); return ans+Query(root,1,z,w[son[y]],w[x]); } int main() { len=0; memset(first,-1,sizeof(first)); scanf("%d",&N); for(int i=1;i<N;i++) { int x,y; scanf("%d%d",&x,&y); ins(x,y,1); ins(y,x,1); } dep[1]=1; Dfs(1); z=0; Dfs1(1,1); tot=0; for(int i=1;i<=z;i++) Link(root,1,z,i,1); int M; scanf("%d",&M); for(int i=1;i<N+M;i++) { char st; scanf(" %c",&st); if(st=='W') { int x; scanf("%d",&x); printf("%d ",Q(1,x)); } else { int x,y; scanf("%d%d",&x,&y); C_(x,y); } } return 0; } /* 5 1 2 1 3 1 4 4 5 4 W 5 A 1 4 W 5 A 4 5 W 5 W 2 A 1 2 A 1 3 */
| [Poi2012]Letters |
统计B串在A串中的位置 找逆序对个数

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<stack> using namespace std; typedef long long LL; const LL Maxn=1000010; LL N; char A[Maxn],B[Maxn]; stack<LL>QA[30]; LL tr[Maxn]; LL low_bit(LL x){return x&(-x);} LL Find(LL x){LL ans=0; for(LL i=x;i;i-=low_bit(i)) ans+=tr[i]; return ans;} void Change(LL x,LL c){for(LL i=x;i<=N;i+=low_bit(i)) tr[i]+=c;} int main() { scanf("%lld",&N); for(LL i=1;i<=N;i++) scanf(" %c",&A[i]); for(LL i=1;i<=N;i++) scanf(" %c",&B[i]); for(LL i=1;i<=N;i++) QA[A[i]-'A'].push(i); LL ans=0; for(LL i=N;i>=1;i--){LL x=QA[B[i]-'A'].top(); ans+=Find(x),QA[B[i]-'A'].pop(),Change(x,1);} return printf("%lld ",ans),0; }
| [HNOI2012]永无乡 |
可持久化权值线段树合并+并查集

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=100010; int lc[Maxn*30],rc[Maxn*30],Sum[Maxn*30]; int tot=0; int rt[Maxn]; void Link(int &u,int L,int R,int k) { if(!u) u=++tot; if(L==R){Sum[u]++; return ;} int mid=(L+R)>>1; if(k<=mid) Link(lc[u],L,mid,k); else Link(rc[u],mid+1,R,k); Sum[u]=Sum[lc[u]]+Sum[rc[u]]; } int N,M; int fa[Maxn]; int Hash[Maxn]; int Find(int x){if(x==fa[x]) return fa[x]; else return fa[x]=Find(fa[x]);} void Merge(int &u1,int u2) { if(!u2) return ; if(!u1){u1=u2; return ;} Merge(lc[u1],lc[u2]); Merge(rc[u1],rc[u2]); Sum[u1]+=Sum[u2]; } int Query(int u,int L,int R,int k) { if(Sum[u]<k) return -1; if(L==R) return L; int mid=(L+R)>>1; if(Sum[lc[u]]>=k) return Query(lc[u],L,mid,k); else return Query(rc[u],mid+1,R,k-Sum[lc[u]]); } int main() { scanf("%d%d",&N,&M); for(int i=1;i<=N;i++) { int x; fa[i]=i; scanf("%d",&x); Link(rt[i],1,300000,x); Hash[x]=i; } for(int i=1;i<=M;i++) { int x,y; scanf("%d%d",&x,&y); int xx=Find(x); int yy=Find(y); if(xx!=yy) { fa[xx]=yy; Merge(rt[yy],rt[xx]); } } scanf("%d",&M); for(int i=1;i<=M;i++) { char st; scanf(" %c",&st); if(st=='Q') { int x,y; scanf("%d%d",&x,&y); int k=Query(rt[Find(x)],1,300000,y); if(k!=-1) printf("%d ",Hash[k]); else printf("%d ",k); } else { int x,y; scanf("%d%d",&x,&y); int xx=Find(x); int yy=Find(y); if(xx!=yy) { fa[xx]=yy; Merge(rt[yy],rt[xx]); } } } return 0; } /* 5 1 4 3 2 5 1 1 2 7 Q 3 2 Q 2 1 B 2 3 B 1 5 Q 2 1 Q 2 4 Q 2 3 */
| [HNOI2015]菜肴制作 |
有一个结论:wph给的题 想好了之后感觉代码长度比他长 90%想错思路或者算法
首先想法是 要最先吃到最优的嘛 所以用结构体记录能去到最优的 和当前的
可是 这样就不能保证次优的了..
后来换思路 我既然不能保证之后是最优和次优的 不妨我倒着建图 选最大的
这样显然正确 选最差的在后面垫着 在前面的要不是管着他的 要不是比它优的
太垃圾了我

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> #include<vector> using namespace std; const int Maxn=100010; struct E { int x,y,next; }edge[Maxn]; int len,first[Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } priority_queue<int>Q; int ru[Maxn]; int T,N,M; vector<int>A; int main() { scanf("%d",&T); while(T--) { scanf("%d%d",&N,&M); len=0; memset(first,-1,sizeof(first)); memset(ru,0,sizeof(ru)); for(int i=1;i<=M;i++) { int x,y; scanf("%d%d",&x,&y); ins(y,x); ru[x]++; } while(!Q.empty()) Q.pop(); for(int i=1;i<=N;i++) if(ru[i]==0) Q.push(i); A.clear(); while(!Q.empty()) { int x=Q.top(); Q.pop(); A.push_back(x); for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; ru[y]--; if(ru[y]==0) Q.push(y); } } if(A.size()!=N) printf("Impossible! "); else{for(int i=A.size()-1;i>=0;i--) printf("%d ",A[i]); printf(" ");} } return 0; }
| [cqoi2013]二进制a+b |
很容易发现a中选一些位+b中选一些位=c中选一些位
之后就是dp咯 F[i][a][b][c][0/1] 分别表示 i位 a中多少个1 .... ... 进不进位
转移显然

#include<cstdio> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; int maxx=0; void G(int x,int &C){int ans=0; while(x){if(x%2) C++; x>>=1; ans++;}maxx=max(maxx,ans);} int A,B,C; int F[40][40][40][40][3]; int main() { scanf("%d%d%d",&A,&B,&C); int A1=0,B1=0,C1=0; G(A,A1); G(B,B1); G(C,C1); memset(F,-63,sizeof(F)); F[0][0][0][0][0]=0; if(A1) F[0][1][0][1][0]=1; if(B1) F[0][0][1][1][0]=1; if(A1&&B1) F[0][1][1][0][1]=2; for(int i=0;i<maxx;i++) for(int a=0;a<=A1;a++) for(int b=0;b<=B1;b++) for(int c=0;c<=C1;c++) { if(F[i][a][b][c][0]>=0) { F[i+1][a+1][b+1][c][1]=F[i][a][b][c][0]+2*(1<<(i+1)); F[i+1][a+1][b][c+1][0]=F[i][a][b][c][0]+(1<<(i+1)); F[i+1][a][b+1][c+1][0]=F[i][a][b][c][0]+(1<<(i+1)); F[i+1][a][b][c][0]=F[i][a][b][c][0]; } if(F[i][a][b][c][1]>=0) { F[i+1][a+1][b+1][c+1][1]=F[i][a][b][c][1]+2*(1<<(i+1)); F[i+1][a+1][b][c][1]=F[i][a][b][c][1]+(1<<(i+1)); F[i+1][a][b+1][c][1]=F[i][a][b][c][1]+(1<<(i+1)); F[i+1][a][b][c+1][0]=F[i][a][b][c][1]; } } if(F[maxx-1][A1][B1][C1][0]>=0) printf("%d ",F[maxx-1][A1][B1][C1][0]); else printf("-1 "); return 0; }
| [HEOI2012]旅行问题 |
ac自动机 然后建fail树lca就是了
为什么呢 最重要的
首先找到两个点 那么他们的fail节点以上的 肯定等于这个点以上的
说明和fail到的节点的后缀是相同的 那么两个后缀相同的 就是公共点
至于要出现过 你在fail都找到节点了 还不出现过吗?

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> #include<vector> using namespace std; typedef long long LL; const int Maxn=1000010; const int Mod=1000000007; struct node { int d,fail,son[26]; LL D; }tr[Maxn]; int rot,tot; void Tnew(int u) { tr[u].d=tr[u].fail=-1; memset(tr[u].son,-1,sizeof(tr[u].son)); } int N,M; string str[Maxn]; vector<int>G[Maxn]; void Build(int k) { int u=rot; LL ans=0; for(int i=0;i<str[k].length();i++) { int j=str[k][i]-'a'; ans=(ans*26+j)%Mod; if(tr[u].son[j]==-1) { Tnew(++tot); tr[u].son[j]=tot; u=tot; tr[u].d=j; } else u=tr[u].son[j]; tr[u].D=ans; G[k].push_back(u); } } queue<int>Q; void AC_Tire() { while(!Q.empty()) Q.pop(); Q.push(rot); while(!Q.empty()) { int u=Q.front(); int j=tr[u].fail; for(int i=0;i<26;i++) { if(tr[u].son[i]==-1) { if(u==rot) tr[u].son[i]=rot; else tr[u].son[i]=tr[j].son[i]; } else { if(u==rot) tr[tr[u].son[i]].fail=rot; else tr[tr[u].son[i]].fail=tr[j].son[i]; Q.push(tr[u].son[i]); } } Q.pop(); } } struct E { int x,y,next; }edge[Maxn]; int len,first[Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } int fa[Maxn][21]; int dep[Maxn]; void Dfs(int x) { for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; dep[y]=dep[x]+1; fa[y][0]=x; Dfs(y); } } int LCA(int x,int y) { if(dep[x]<dep[y]) swap(x,y); int deep=dep[x]-dep[y]; for(int i=20;i>=0;i--) if(deep>=(1<<i)) deep-=(1<<i),x=fa[x][i]; if(x==y) return x; for(int i=20;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; } int main() { scanf("%d",&N); rot=tot=1; Tnew(tot); for(int i=1;i<=N;i++) { cin>>str[i]; Build(i); } AC_Tire(); len=0; memset(first,-1,sizeof(first)); for(int i=2;i<=tot;i++) ins(tr[i].fail,i); memset(dep,0,sizeof(dep)); dep[rot]=1; Dfs(rot); for(int j=1;j<=20;j++) for(int i=1;i<=tot;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; scanf("%d",&M); for(int K=1;K<=M;K++) { int i,j,k,l; scanf("%d%d%d%d",&i,&j,&k,&l); int x=G[i][j-1]; int y=G[k][l-1]; int L=LCA(x,y); printf("%lld ",tr[L].D); } return 0; } /* 2 aabb babb 2 1 3 2 3 1 4 2 4 */
| [JLOI2011]基因补全 |
简单dp F[i][j]表示长的前i位中匹配短的前j位 不一定是刚好那一位 初始化就把j=1扫一遍即可
高精压位补零

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<ctime> using namespace std; const int Maxn=2010; struct node { int A[50],len; friend node operator+(const node &x,const node &y) { node z; z.len=max(x.len,y.len); for(int i=1;i<=z.len;i++) z.A[i]=x.A[i]+y.A[i]; for(int i=1;i<=z.len;i++) if(z.A[i]>=100000000){z.A[i+1]+=z.A[i]/100000000; z.A[i]%=100000000;} while(z.A[z.len+1]) z.len++; return z; } node(){memset(A,0,sizeof(A)); len=1;} }F[Maxn][2]; int ST=1; int N,M; char A[Maxn],B[Maxn]; bool bo(char x,char y) { if(x=='A'&&y=='T') return 1; if(x=='C'&&y=='G') return 1; if(x=='T'&&y=='A') return 1; if(x=='G'&&y=='C') return 1; return 0; } int main() { scanf("%d%d",&N,&M); for(int i=1;i<=N;i++) scanf(" %c",&A[i]); for(int i=1;i<=M;i++) scanf(" %c",&B[i]); if(N<M){swap(N,M); for(int i=1;i<=N;i++) swap(A[i],B[i]);} for(int i=1;i<=N;i++) { F[i][1]=(F[i][1]+F[i-1][1]); if(bo(A[i],B[1])) { F[i][1].A[1]++; int p=1; while(F[i][1].A[p]>=100000000){F[i][1].A[p+1]+=F[i][1].A[p]/100000000; F[i][1].A[p]%=100000000; p++;} while(F[i][1].A[F[i][1].len+1]) F[i][1].len++; } } for(int j=2;j<=M;j++) { ST=1-ST; for(int i=1;i<=N;i++) F[i][ST].len=1,memset(F[i][ST].A,0,sizeof(F[i][ST].A)); for(int i=1;i<=N;i++) { F[i][ST]=F[i][ST]+F[i-1][ST]; if(bo(A[i],B[j])) F[i][ST]=F[i-1][1-ST]+F[i][ST]; } } printf("%d",F[N][ST].A[F[N][ST].len]); for(int i=F[N][ST].len-1;i>=1;i--) printf("%08d",F[N][ST].A[i]); return printf(" "),0; }
| [HAOI2010]计数 |
去0之后添零 本来想着组合一下dp一下再dfs一下
后来发现错了 其实是很简单的一个数位dp
满不满 有没有前导0就好,其他情况可以快速算
n!/(a1!*a2!*.....*an!) 组合数学
其实好像想了想要不要有前导0好像都没所谓...
乘的时候用分解质因数

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Maxn=100; char st[Maxn]; LL len; LL F[Maxn][Maxn]; LL num[Maxn]; LL S[Maxn]={0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47}; LL C[Maxn]; LL Dfs(LL step,bool pA,bool pB) //zero and exist { if(step==len) return 1; if(pB==0&&pA==0) { LL N=len-step; for(LL i=1;i<=N;i++) { LL x=i; if(!x) continue; for(LL j=1;j<=15;j++) while(!(x%S[j])) x/=S[j],C[j]++; } for(LL i=0;i<=9;i++) { for(LL k=1;k<=num[i];k++) { LL x=k; if(!x) continue; for(LL j=1;j<=15;j++) while(!(x%S[j])) x/=S[j],C[j]--; } } LL tot=1; for(LL j=1;j<=15;j++) while(C[j]) C[j]--,tot*=S[j]; return tot; } else if(pB) { LL tot=0; for(LL i=0;i<=st[step+1]-'0';i++) { bool bB; if(i==st[step+1]-'0'&&pB) bB=1; else bB=0; if(num[i]) {num[i]--; tot+=Dfs(step+1,pA,bB); num[i]++;} }return tot; } else if(pA) { LL tot=0; for(LL i=0;i<=9;i++) { bool bA; if(i==0&&pA) bA=1; else bA=0; if(num[i]) {num[i]--; tot+=Dfs(step+1,bA,pB); num[i]++;} }return tot; } } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); scanf("%s",st+1); len=strlen(st+1); memset(num,0,sizeof(num)); for(LL i=1;i<=len;i++) num[st[i]-'0']++; LL tot=0; memset(C,0,sizeof(C)); for(LL i=0;i<=st[1]-'0';i++) { bool pA,pB; if(i==0) pA=1; else pA=0; if(i==st[1]-'0') pB=1; else pB=0; if(num[i]) {num[i]--; tot+=Dfs(1,pA,pB); num[i]++;} } return printf("%lld ",tot-1),0; }
| [Poi2012]A Horrible Poem |
真jj蛋疼这道题
sa和rmq一下 然后更号枚举长度超时
加优化

这样枚举重复次数 然后算出重复长度

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=500010; int N; char str[Maxn]; int fir[Maxn],sec[Maxn],A[Maxn],rank[Maxn],sa[Maxn],R[Maxn]; void Rsort(int *use,int *in,int *out,int size,int num) { for(int i=1;i<=size;i++) R[i]=0; for(int i=1;i<=num;i++) R[use[in[i]]]++; for(int i=1;i<=size;i++) R[i]+=R[i-1]; for(int i=num;i>=1;i--) out[R[use[in[i]]]--]=in[i]; } void SA() { for(int i=1;i<=N;i++) rank[i]=i; Rsort(A,rank,sa,300,N); rank[sa[1]]=1; for(int i=2;i<=N;i++) rank[sa[i]]=rank[sa[i-1]]+(A[sa[i]]!=A[sa[i-1]]); int p=0; int cnt=1; while(cnt<N) { for(int i=1;i<=N;i++) { fir[i]=rank[i]; sec[i]=(i+(1<<p))>N?0:rank[(i+(1<<p))]; sa[i]=i; } Rsort(sec,sa,rank,N,N); Rsort(fir,rank,sa,N,N); rank[sa[1]]=1; for(int i=2;i<=N;i++) rank[sa[i]]=rank[sa[i-1]]+((fir[sa[i]]!=fir[sa[i-1]])||(sec[sa[i]]!=sec[sa[i-1]])); p++; cnt=rank[sa[N]]; } } int H[Maxn][20]; void Height() { int p=0; for(int i=1;i<=N;i++) { if(p) p--; if(rank[i]!=1) { int pos=sa[rank[i]-1]; while(A[pos+p]==A[i+p]) p++; }H[rank[i]][0]=p; } } int ls[Maxn]; void RMQ() { for(int j=1;j<=20;j++) for(int i=1;i<=N;i++) if(i>=(1<<j)) H[i][j]=min(H[i][j-1],H[i-(1<<(j-1))][j-1]); } int pre[Maxn][27]; int gcd(int x,int y){if(y==0) return x; else return gcd(y,x%y);} int main() { scanf("%d",&N); for(int i=1;i<=N;i++){scanf(" %c",&str[i]); A[i]=str[i];} SA(); Height(); RMQ(); int M; scanf("%d",&M); for(int i=1;i<=N;i++){for(int j=1;j<=26;j++) pre[i][j]+=pre[i-1][j]; pre[i][A[i]-'a'+1]++;} for(int i=0;(1<<i)<=N;i++) ls[1<<i]=i; for(int i=1;i<=N;i++) if(!ls[i]) ls[i]=ls[i-1]; for(int i=1;i<=M;i++) { int x,y; scanf("%d%d",&x,&y); int L=y-x+1; int minx=L; int m=L; for(int j=1;j<=26;j++) if(pre[y][j]!=pre[x-1][j]) m=gcd(m,(pre[y][j]-pre[x-1][j])); for(int j=1;j<=sqrt(m);j++) if(m%j==0) { int L1=L/(m/j); if((m/j)*L1!=L) continue; if(L1<minx) { int l,r,D,Suffix; l=rank[x]; r=rank[x+L1]; if(l<r) swap(l,r); D=l-r; Suffix=min(L-L1,min(H[l][ls[D]],H[r+(1<<ls[D])][ls[D]])); if(Suffix==L-L1) minx=min(minx,L1); } int L2=L/j; if(j*L2!=L) continue; if(L2<minx) { int l,r,D,Suffix; l=rank[x]; r=rank[x+L2]; if(l<r) swap(l,r); D=l-r; Suffix=min(L-L2,min(H[l][ls[D]],H[r+(1<<ls[D])][ls[D]])); if(Suffix==L-L2) minx=min(minx,L2); } } printf("%d ",minx); } return 0; } /* 8 aaabcabc 3 1 3 3 8 4 8 */
| [HAOI2012]容易题(easy) |
积的和等于和的积
数据范围告诉我们不是容斥 把删去的不算 快速幂+扫一遍即可

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<vector> #include<map> using namespace std; typedef long long LL; const LL Mod=1000000007; const LL Maxn=1e5+10; LL N,M,K; map<LL,LL>mp; LL tot; vector<LL>V[Maxn]; LL bas; LL Quick(LL x) { if(x==1) return bas%Mod; if(x==0) return 1; LL ans=Quick(x>>1)%Mod; if(x&1) return ((bas*ans)%Mod*ans)%Mod; else return ans*ans%Mod; } int main() { scanf("%lld%lld%lld",&N,&M,&K); tot=0; for(LL i=1;i<=K;i++) { LL x,y; scanf("%lld%lld",&x,&y); if(mp[x]==0) mp[x]=++tot; V[mp[x]].push_back(y); } bas=((N+1)*N/2)%Mod; LL ans=Quick(M-tot); for(LL i=1;i<=tot;i++) { sort(V[i].begin(),V[i].end()); LL len=unique(V[i].begin(),V[i].end())-V[i].begin(); LL s=bas; for(LL j=0;j<len;j++) { s-=V[i][j]; if(s<0) s+=Mod; } ans=(ans*s)%Mod; } return printf("%lld ",ans),0; } /* 3 4 5 1 1 1 1 2 2 2 3 4 3 */
| [Sdoi2016]排列计数 |
组合错排逆元 预处理阶乘

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Maxn=1000010; const LL Mod=1e9+7; LL N,M; LL T; LL D[Maxn]; LL C[Maxn],ny[Maxn]; void exgcd(LL a,LL b,LL &x,LL &y) { if(b==0){x=1; y=0; return ;} else { LL tx,ty; exgcd(b,a%b,tx,ty); x=ty; y=tx-a/b*ty; } } int main() { scanf("%lld",&T); D[0]=1; D[1]=0; D[2]=1; D[3]=2; for(LL i=4;i<=1000000;i++) D[i]=(i-1)*(D[i-1]+D[i-2])%Mod; C[0]=C[1]=1; for(LL i=2;i<=1000000;i++) C[i]=C[i-1]*i%Mod; for(LL i=0;i<=1000000;i++) { LL x,y; exgcd(C[i],Mod,x,y); ny[i]=((x%Mod)+Mod)%Mod; } while(T--) { scanf("%lld%lld",&N,&M); printf("%lld ",((C[N]*ny[M])%Mod*ny[N-M])%Mod*D[N-M]%Mod); } return 0; }
| [Sdoi2016]数字配对 |
A得好悬啊
很容易发现是费用流 直接分两边构图显然不行 想办法把点分两边
考虑分解质因数的个数的奇偶来建二分图
跑费用流的时候把费用取反 大于0时跳出来
然后注意就是最后一次跑的时候 因为跑的是最大流 导致不满足 适当调节流量满足条件即可

#include <cstdio> #include <iostream> #include <cstring> #include <algorithm> #include <cstdlib> #include <cmath> #include <vector> #include <queue> #include <climits> using namespace std; typedef long long LL; const LL Maxn=210; const LL inf=1e10+7; struct node { LL x,y,next,c,d,other; }edge[Maxn*Maxn*10]; LL len,first[Maxn*Maxn]; void ins(LL x,LL y,LL c,LL d) { len++; LL k1=len; edge[len].x=x; edge[len].y=y; edge[len].c=c; edge[len].d=d; edge[len].next=first[x]; first[x]=len; len++; LL k2=len; edge[len].x=y; edge[len].y=x; edge[len].c=0; edge[len].d=-d; edge[len].next=first[y]; first[y]=len; edge[k1].other=k2; edge[k2].other=k1; } LL A[Maxn],B[Maxn],C[Maxn],O[Maxn]; LL N; LL ST,ED; LL prime[32010],phi; bool bo[32010]; void Prime() { phi=0; memset(prime,0,sizeof(prime)); memset(bo,1,sizeof(bo)); bo[0]=bo[1]=0; for(LL i=2;i<=32000;i++) { if(bo[i]){prime[++phi]=i;} for(LL j=1;(j<=phi)&&(i*prime[j]<=32000);j++) { bo[i*prime[j]]=0; if(i%prime[j]==0) break; } } } LL D[Maxn],pre[Maxn],pos[Maxn]; queue<LL>Q; bool V[Maxn]; bool Spfa() { memset(D,126,sizeof(D)); D[ST]=0; memset(pre,0,sizeof(pre)); memset(pos,0,sizeof(pos)); memset(V,0,sizeof(V)); V[ST]=1; while(!Q.empty()) Q.pop(); Q.push(ST); while(!Q.empty()) { LL x=Q.front(); for(LL k=first[x];k!=-1;k=edge[k].next) { LL y=edge[k].y; if(D[y]>D[x]+edge[k].d&&edge[k].c) { pre[y]=k; pos[y]=x; D[y]=D[x]+edge[k].d; if(!V[y]){V[y]=1; Q.push(y);} } } Q.pop(); V[x]=false; } return D[ED]<inf; } int main() { scanf("%lld",&N); len=0; memset(first,-1,sizeof(first)); for(LL i=1;i<=N;i++) scanf("%lld",&A[i]); for(LL i=1;i<=N;i++) scanf("%lld",&B[i]); for(LL i=1;i<=N;i++) scanf("%lld",&C[i]); ST=N+1; ED=N+2; Prime(); for(LL i=1;i<=N;i++) { O[i]=0; LL x=A[i]; for(LL j=1;j<=phi;j++) while(x%prime[j]==0) x/=prime[j],O[i]++; if(x!=1) O[i]++,x=1; if(O[i]&1) ins(ST,i,B[i],0); else ins(i,ED,B[i],0); } for(LL i=1;i<=N;i++) for(LL j=1;j<=N;j++) { if((A[i]%A[j]==0)&&(O[i]-O[j]==1)) { if(O[i]&1) ins(i,j,inf,-C[i]*C[j]); else ins(j,i,inf,-C[i]*C[j]); } if((A[j]%A[i]==0)&&(O[j]-O[i]==1)) { if(O[i]&1) ins(i,j,inf,-C[i]*C[j]); else ins(j,i,inf,-C[i]*C[j]); } } LL ans=0; LL delta=0; while(Spfa()) { LL minf=LONG_MAX; LL D=0; for(LL i=ED;i!=ST;i=pos[i]) minf=min(minf,edge[pre[i]].c); for(LL i=ED;i!=ST;i=pos[i]) D+=edge[pre[i]].d; if(D>0) minf=min(minf,(0-ans)/D); for(LL i=ED;i!=ST;i=pos[i]) ans+=minf*edge[pre[i]].d; for(LL i=ED;i!=ST;i=pos[i]) edge[pre[i]].c-=minf,edge[edge[pre[i]].other].c+=minf; if(minf==0) break; else delta+=minf; } return printf("%lld ",delta),0; } /* 3 2 4 8 2 200 7 -1 -2 1 */
| [Sdoi2016]生成魔咒 |
反串做后缀数组 表示不会sam

#include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> #include<vector> #include<map> using namespace std; typedef long long LL; const int Maxn=100010; int N; int B[Maxn]; int A[Maxn]; int fir[Maxn],sec[Maxn],sa[Maxn],height[Maxn],rank[Maxn],R[Maxn]; void Rsort(int *use,int *in,int *out,int size,int num) { for(int i=0;i<=size;i++) R[i]=0; for(int i=1;i<=num;i++) R[use[in[i]]]++; for(int i=1;i<=size;i++) R[i]+=R[i-1]; for(int i=num;i>=1;i--) out[R[use[in[i]]]--]=in[i]; } void SA() { for(int i=1;i<=N;i++) rank[i]=i; Rsort(A,rank,sa,100000,N); rank[sa[1]]=1; for(int i=2;i<=N;i++) rank[sa[i]]=rank[sa[i-1]]+(A[sa[i]]!=A[sa[i-1]]); int p=0; int cnt=1; while(cnt<N) { for(int i=1;i<=N;i++) { fir[i]=rank[i]; sec[i]=(i+(1<<p)>N)?0:rank[i+(1<<p)]; sa[i]=i; } Rsort(sec,sa,rank,N,N); Rsort(fir,rank,sa,N,N); rank[sa[1]]=1; for(int i=2;i<=N;i++) rank[sa[i]]=rank[sa[i-1]]+((fir[sa[i]]!=fir[sa[i-1]])||(sec[sa[i]]!=sec[sa[i-1]])); cnt=rank[sa[N]]; p++; } } int H[Maxn][20]; void Height() { int p=0; for(int i=1;i<=N;i++) { if(p) p--; if(rank[i]!=1) { int pos=sa[rank[i]-1]; while(A[pos+p]==A[i+p]) p++; }H[rank[i]][0]=p; } } void RMQ() { for(int j=1;j<=20;j++) for(int i=(1<<j)+1;i<=N;i++) H[i][j]=min(H[i][j-1],H[i-(1<<(j-1))][j-1]); } int lc[Maxn*4],rc[Maxn*4]; int root,tot=0; int C[Maxn*4]; int Low(int u,int L,int R,int l,int r) { if(!u) return -1; if(l>r) return -1; if(L==l&&R==r) { int uu=u; while(1) { int mid=(L+R)>>1; if(L==R) return L; if(C[rc[uu]]) uu=rc[uu],L=mid+1; else uu=lc[uu],R=mid; } } int mid=(L+R)>>1; if(r<=mid) return Low(lc[u],L,mid,l,r); else if(l>mid) return Low(rc[u],mid+1,R,l,r); else { int k1=Low(lc[u],L,mid,l,mid); int k2=Low(rc[u],mid+1,R,mid+1,r); if(k2!=-1) return k2; else return k1; } } int UP(int u,int L,int R,int l,int r) { if(!u) return -1; if(l>r) return -1; if(L==l&&R==r) { int uu=u; while(1) { int mid=(L+R)>>1; if(L==R) return L; if(C[lc[uu]]) uu=lc[uu],R=mid; else uu=rc[uu],L=mid+1; } } int mid=(L+R)>>1; if(r<=mid) return UP(lc[u],L,mid,l,r); else if(l>mid) return UP(rc[u],mid+1,R,l,r); else { int k1=UP(lc[u],L,mid,l,mid); int k2=UP(rc[u],mid+1,R,mid+1,r); if(k1!=-1) return k1; else return k2; } } void Link(int &u,int L,int R,int k) { if(!u) u=++tot; if(L==R){C[u]++; return ;} int mid=(L+R)>>1; if(k<=mid) Link(lc[u],L,mid,k); else Link(rc[u],mid+1,R,k); C[u]=C[lc[u]]+C[rc[u]]; } int bit[Maxn]; int G(int l,int r) { int D=r-l; return min(H[r][bit[D]],H[l+(1<<bit[D])][bit[D]]); } map<int,int>mp; vector<int>V; int main() { scanf("%d",&N); for(int i=1;i<=N;i++){scanf("%d",&B[i]); V.push_back(B[i]);} sort(V.begin(),V.end()); int len=unique(V.begin(),V.end())-V.begin(); for(int i=0;i<len;i++) mp[V[i]]=i+1; for(int i=N;i>=1;i--) A[i]=mp[B[N-i+1]]; SA(); Height(); RMQ(); for(int i=0;i<=16;i++) bit[1<<i]=i; for(int i=1;i<=100000;i++) if(!bit[i]) bit[i]=bit[i-1]; memset(C,0,sizeof(C)); LL ans=0; for(int i=N;i>=1;i--) { int now=rank[i]; int D=Low(root,1,N,1,now-1); int U=UP(root,1,N,now+1,N); int s=0; if(U!=-1) s=max(s,G(now,U)); if(D!=-1) s=max(s,G(D,now)); ans+=(N-i+1-s); printf("%lld ",ans); Link(root,1,N,now); } return 0; }
| [Shoi2010]最小生成树 |
我太垃圾了 没想到这题
一定用到这条边 也就是这条边之前两个端点没有联通 就是把这两个端点一个作源一个作汇 然后把之前的边建上 跑最小割
其他的边减流量就是那一条边加流量

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<queue> #include<climits> using namespace std; const int Maxn=810; struct node { int x,y,next,c,other; }edge[Maxn*Maxn]; int len,first[Maxn]; void ins(int x,int y,int c) { len++; int k1=len; edge[len].x=x; edge[len].y=y; edge[len].c=c; edge[len].next=first[x]; first[x]=len; len++; int k2=len; edge[len].x=y; edge[len].y=x; edge[len].c=c; edge[len].next=first[y]; first[y]=len; edge[k1].other=k2; edge[k2].other=k1; } int dep[Maxn]; queue<int>Q; int ST,ED; bool Bfs() { memset(dep,0,sizeof(dep)); dep[ST]=1; while(!Q.empty()) Q.pop(); Q.push(ST); while(!Q.empty()) { int x=Q.front(); for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(edge[k].c&&dep[y]==0) { dep[y]=dep[x]+1; Q.push(y); } } Q.pop(); } return dep[ED]>0; } int Dfs(int x,int Flow) { if(x==ED) return Flow; int delta=0; for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(dep[y]==dep[x]+1&&edge[k].c&&Flow>delta) { int minf=Dfs(y,min(Flow-delta,edge[k].c)); edge[k].c-=minf; edge[edge[k].other].c+=minf; delta+=minf; } } if(delta==0) dep[x]=0; return delta; } int N,M,Lab; int X[Maxn],Y[Maxn],D[Maxn]; int main() { scanf("%d%d%d",&N,&M,&Lab); len=0; memset(first,-1,sizeof(first)); for(int i=1;i<=M;i++) scanf("%d%d%d",&X[i],&Y[i],&D[i]); ST=X[Lab]; ED=Y[Lab]; for(int i=1;i<=M;i++) if(D[i]<=D[Lab]&&i!=Lab) ins(X[i],Y[i],D[Lab]-D[i]+1); int ans=0,delta; while(Bfs()) { if(delta=Dfs(ST,INT_MAX)) ans+=delta; } return printf("%d ",ans),0; }
| [Poi2012]Warehouse Store |
能取的取 不能取的换 usaco原题
一开始想错了 直接取最小的 能取就取 没有考虑最小的对后面的影响..

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<queue> #include<vector> using namespace std; typedef long long LL; const LL Maxn=250010; priority_queue<pair<LL,LL> >Q; LL A[Maxn],B[Maxn],N; vector<LL>V; int main() { //freopen("a.in","r",stdin); //freopen("a.out","w",stdout); scanf("%lld",&N); for(LL i=1;i<=N;i++) scanf("%lld",&A[i]); for(LL i=1;i<=N;i++) scanf("%lld",&B[i]); LL sum=0; LL ans=0; for(LL i=1;i<=N;i++) { sum+=A[i]; if(sum>B[i]){sum-=B[i]; ans++; Q.push(make_pair(B[i],i));} else { pair<LL,LL> x; if(!Q.empty()) { x=Q.top(); if(B[i]<x.first) Q.pop(),Q.push(make_pair(B[i],i)),sum+=x.first-B[i]; } } } printf("%lld ",ans); while(!Q.empty()) V.push_back(Q.top().second),Q.pop(); sort(V.begin(),V.end()); for(LL i=0;i<V.size();i++) printf("%lld ",V[i]); return 0; }
| [Poi2012]Fibonacci Representation |
很容易证明答案肯定是减恰好小于这个数或者恰好大于这个数的减这个数
目测递归可以做 随便搞一下

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<climits> using namespace std; typedef long long LL; const LL inf=1e18; const LL Maxn=200; LL T,N; LL A[Maxn]; LL tot=0; LL minx; void Dfs(LL x,LL step) { if(x==0){minx=min(minx,step); return ;} if(step>=minx) return ; LL D=lower_bound(A+1,A+tot+1,x)-(A+1); LL U=lower_bound(A+1,A+tot+1,x)-(A+1)+1; Dfs(x-A[D],step+1); Dfs(A[U]-x,step+1); } int main() { A[0]=1; A[1]=1; A[2]=1; tot=2; for(LL i=3;(A[i-1]<=inf);i++) A[i]=A[i-1]+A[i-2],tot++; scanf("%lld",&T); while(T--) { scanf("%lld",&N); minx=LONG_MAX; Dfs(N,0); printf("%lld ",minx); } return 0; }
| [Poi2012]Cloakroom |
离线背包存b

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<climits> using namespace std; const int Maxn=1010; struct node { int A,B,C; }obj[Maxn]; struct Que { int m,k,s,id; }Q[1000010]; bool ans[1000010]; bool Cmp(const node &x,const node &y){if(x.A!=y.A) return x.A<y.A; return x.B>y.B;} bool Cmp1(const Que &x,const Que &y){return x.m<y.m;} int N,M; int H[100010]; int main() { //freopen("a.in","r",stdin); //freopen("a.out","w",stdout); scanf("%d",&N); for(int i=1;i<=N;i++) scanf("%d%d%d",&obj[i].C,&obj[i].A,&obj[i].B); sort(obj+1,obj+N+1,Cmp); scanf("%d",&M); for(int i=1;i<=M;i++){scanf("%d%d%d",&Q[i].m,&Q[i].k,&Q[i].s); Q[i].id=i;} sort(Q+1,Q+M+1,Cmp1); int o=1; memset(H,-1,sizeof(H)); H[0]=INT_MAX; for(int i=1;i<=M;i++) { while(o<=N&&obj[o].A<=Q[i].m) { for(int j=100000;j>=obj[o].C;j--) if(H[j-obj[o].C]>-1) H[j]=max(H[j],min(H[j-obj[o].C],obj[o].B)); o++; } if(H[Q[i].k]>Q[i].m+Q[i].s) ans[Q[i].id]=1; else ans[Q[i].id]=0; } for(int i=1;i<=M;i++) if(ans[i]) printf("TAK "); else printf("NIE "); return 0; } /* 5 6 2 7 5 4 9 1 2 4 2 5 8 1 3 9 5 2 7 1 2 7 2 3 2 0 5 7 2 4 1 5 */
| [HAOI2012]音量调节 |
二维扫一下

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=1010; int N,B,M; int C[Maxn]; bool bo[Maxn][Maxn]; int main() { scanf("%d%d%d",&N,&B,&M); for(int i=1;i<=N;i++) scanf("%d",&C[i]); memset(bo,0,sizeof(bo)); bo[0][B]=1; for(int i=1;i<=N;i++) { for(int j=0;j<=M;j++) { if(bo[i-1][j]) { if(j-C[i]>=0) bo[i][j-C[i]]=1; if(j+C[i]<=M) bo[i][j+C[i]]=1; } } } int maxx=-1; for(int i=0;i<=M;i++) if(bo[N][i]) maxx=max(maxx,i); return printf("%d ",maxx),0; }
| 可持久化并查集 by zky |
| [Scoi2010]字符串 |
和卡特兰数模型有点相像 究其根源就好
Catalan: http://blog.chinaunix.net/uid-26456800-id-3462158.html

#include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Maxn=2000010; const LL Mod=20100403; LL N,M; LL S[Maxn]; void exgcd(LL a,LL b,LL &x,LL &y) { if(b==0){x=1; y=0; return ;} else { LL tx,ty; exgcd(b,a%b,tx,ty); x=ty; y=tx-a/b*ty; } } LL ny(LL i) { LL X,Y; exgcd(S[i],Mod,X,Y); X=(X%Mod+Mod)%Mod; return X; } int main() { scanf("%lld%lld",&N,&M); S[1]=1; for(LL i=2;i<=2000000;i++) S[i]=(S[i-1]*i)%Mod; LL Q=M+N; LL X1=(S[Q]*ny(N)%Mod*ny(Q-N)%Mod); LL X2=(S[Q]*ny(N+1)%Mod*ny(Q-N-1)%Mod); return printf("%lld ",((X1-X2)%Mod+Mod)%Mod),0; }
| [AHOI2012]树屋阶梯 |
卡特兰数 画图很容易证明 好像是维基有 然后很感人肺腑的是别人用python写了几b的代码我写1.5kb的高精度

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Maxn=1010; LL prime[Maxn],phi; bool V[Maxn]; void Prime() { memset(V,1,sizeof(V)); V[1]=0; phi=0; for(LL i=2;i<=1000;i++) { if(V[i]) V[i]=false,prime[++phi]=i; for(LL j=1;(i*prime[j]<=1000);j++) { V[i*prime[j]]=0; if(i%prime[j]==0) break; } } } LL A[Maxn]; LL Alen=0; LL Sum[Maxn]; LL N; void Mul(LL x) { for(LL i=1;i<=Alen;i++) A[i]*=x; for(LL i=1;i<=Alen;i++) { A[i+1]+=A[i]/10; A[i]%=10; if(A[Alen+1]>0) Alen++; } } int main() { Prime(); scanf("%lld",&N); memset(Sum,0,sizeof(Sum)); for(LL i=1;i<=2*N;i++) { LL x=i; for(LL j=1;j<=phi;j++) while(x%prime[j]==0) { x/=prime[j]; Sum[prime[j]]++; } } for(LL i=1;i<=N;i++) { LL x=i; for(LL j=1;j<=phi;j++) while(x%prime[j]==0) { x/=prime[j]; Sum[prime[j]]--; } } for(LL i=1;i<=N+1;i++) { LL x=i; for(LL j=1;j<=phi;j++) while(x%prime[j]==0) { x/=prime[j]; Sum[prime[j]]--; } } Alen=1; A[1]=1; for(LL i=1;i<=phi;i++) while(Sum[prime[i]]) { Sum[prime[i]]--,Mul(prime[i]); } for(LL i=Alen;i>=1;i--) printf("%lld",A[i]); return printf(" "),0; }
| [Usaco2012 Dec]First! |
拓扑搞一下 之前好像做过 然后一直RE 今天发现改用scanf printf就AC了草你妈的

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<vector> #include<queue> #include<ctime> using namespace std; const int Maxn=30010; struct node { int bk,son[30]; }tr[Maxn*10]; int tot,rot; char str[Maxn][30]; int N; bool G[30][30]; int ru[30]; void ins(int x,int y){G[x][y]=1; ru[y]++;} int Q[30],head,tail; bool Topo() { head=1; tail=0; for(int i=0;i<26;i++) if(ru[i]==0) Q[++tail]=i; while(head<=tail) { int x=Q[head]; for(int y=0;y<26;y++) if(G[x][y]) { ru[y]--; if(!ru[y]) Q[++tail]=y; } head++; } for(int i=0;i<26;i++) if(ru[i]) return false; return true; } int A[Maxn]; int Alen; int main() { scanf("%d",&N); tot=rot=1; for(int i=1;i<=N;i++) { scanf("%s",str[i]); int u=rot; int len=strlen(str[i]); for(int j=0;j<len;j++) { if(!tr[u].son[str[i][j]-'a']) tr[u].son[str[i][j]-'a']=++tot; u=tr[u].son[str[i][j]-'a']; } tr[u].bk=1; } Alen=0; for(int i=1;i<=N;i++) { int u=rot; memset(G,0,sizeof(G)); memset(ru,0,sizeof(ru)); bool bk=true; int len=strlen(str[i]); for(int j=0;j<len;j++) { int k=str[i][j]-'a'; if(tr[u].bk){bk=false; break;} for(int l=0;l<26;l++) { if(l==k) continue; if(tr[u].son[l]&&(!G[k][l])) ins(k,l); } u=tr[u].son[k]; } if(bk) bk=Topo(); if(bk) A[++Alen]=i; } printf("%d ",Alen); for(int i=1;i<=Alen;i++) printf("%s ",str[A[i]]); //cout<<(double)(clock())<<endl; return 0; } /* 4 omm moo mom ommnom */
| 可持久化并查集 by zky |
见wph模板

#include<cstdio> #include<iostream> #include<cstdlib> #include<cstring> #include<cmath> #include<ctime> #include<algorithm> #include<queue> #include<vector> #include<stack> #include<set> #include<ext/rope> using namespace std; using namespace __gnu_cxx; const int Maxn=200100; int N,M,F[Maxn]; rope<int>Fa[Maxn]; int Find(int i,int x) { if(Fa[i].at(x)==x) return x; return Fa[i].replace(x,Find(i,Fa[i].at(x))),Fa[i].at(x); } void Merge(int i,int x,int y) { int xx=Find(i,x); int yy=Find(i,y); Fa[i].replace(xx,yy); } int main() { scanf("%d%d",&N,&M); int lastans=0; for(int i=1;i<=N;i++) F[i]=i; Fa[0]=rope<int>(F,F+N+1); for(int i=1;i<=M;i++) { int opt; scanf("%d",&opt); Fa[i]=rope<int>(Fa[i-1]); if(opt==1) { int X,Y; scanf("%d%d",&X,&Y); X^=lastans; Y^=lastans; Merge(i,X,Y); } else if(opt==2) { int K; scanf("%d",&K); K^=lastans; Fa[i]=Fa[K]; } else { int X,Y; scanf("%d%d",&X,&Y); X^=lastans; Y^=lastans; if(Find(i,X)==Find(i,Y)) printf("1 "); else printf("0 "); } } return 0; }
| 可持久化并查集加强版 |
之前MLE了几发 后来听wph大神说replace占空间..
不用指针会RE
重新规范一下写法

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<ext/rope> using namespace std; using namespace __gnu_cxx; const int Maxn=200010; int F[Maxn]; rope<int> *Fa[Maxn]; int Find(int i,int x) { if(Fa[i]->at(x)==x) return x; int Fz=Find(i,Fa[i]->at(x)); if(Fz!=Fa[i]->at(x)) Fa[i]->replace(x,Fz); return Fz; } int N,M; int main() { scanf("%d%d",&N,&M); int lastans=0; for(int i=1;i<=N;i++) F[i]=i; Fa[0]=new rope<int>(F,F+N+1); for(int i=1;i<=M;i++) { int opt; scanf("%d",&opt); Fa[i]=new rope<int>(* Fa[i-1]); if(opt==1) { int x,y; scanf("%d%d",&x,&y); x^=lastans; y^=lastans; int xx=Find(i,x); int yy=Find(i,y); if(xx!=yy) Fa[i]->replace(xx,yy); } else if(opt==2) { int k; scanf("%d",&k); k^=lastans; Fa[i]=Fa[k]; } else if(opt==3) { int x,y; scanf("%d%d",&x,&y); x^=lastans; y^=lastans; if(Find(i,x)!=Find(i,y)) printf("0 "),lastans=0; else printf("1 "),lastans=1; } } return 0; } /* 5 6 1 1 2 3 1 2 2 1 3 0 3 2 1 3 1 2 */
| [Poi2012]Distance |
线筛质因数个数F[]
很容易得到要使F[i]+F[j]-F[gcd(i,j)]最小 所以先用每个数更新gcd 的记录最小和次小 然后再用每个数找
垃圾sqrt毁我青春狗屁

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<climits> #include<ctime> using namespace std; const int Maxn=1e6+10; int N,A[Maxn]; int F[Maxn]; int prime[Maxn],phi; bool V[Maxn]; void Pre() { memset(F,0,sizeof(F)); memset(V,1,sizeof(V)); V[1]=0; for(int i=2;i<=1000000;i++) { if(V[i]){prime[++phi]=i; F[i]=1; V[i]=false;} for(int j=1;(j<=phi)&&((prime[j]*i)<=1000000);j++) { V[i*prime[j]]=0; F[i*prime[j]]=F[i]+1; if(i%prime[j]==0) break; } } } int fir[Maxn],sec[Maxn]; int Read() { int f=1,p=0; char c=getchar(); while(c>'9'||c<'0'){if(c=='-') f=-1; c=getchar();} while(c>='0'&&c<='9'){p=p*10+c-'0'; c=getchar();} return f*p; } int main() { N=Read(); for(int i=1;i<=N;i++) A[i]=Read(); Pre(); for(int i=1;i<=N;i++) { for(int j=1;j*j<=A[i];j++) { if(A[i]%j==0) { if((!fir[j])||(F[A[fir[j]]]>F[A[i]])){sec[j]=fir[j]; fir[j]=i;} else if((!sec[j])||(F[A[sec[j]]]>F[A[i]])) sec[j]=i; int jj=A[i]/j; if(jj==j) continue; if((!fir[jj])||(F[A[fir[jj]]]>F[A[i]])){sec[jj]=fir[jj]; fir[jj]=i;} else if((!sec[jj])||(F[A[sec[jj]]]>F[A[i]])) sec[jj]=i; } } } for(int i=1;i<=N;i++) { int minx=INT_MAX; int p=-1; for(int j=1;j*j<=A[i];j++) { if(A[i]%j==0) { if(fir[j]) { if(fir[j]!=i) { if((F[A[i]]+F[A[fir[j]]]-2*F[j]==minx)&&(p>fir[j])) minx=F[A[i]]+F[A[fir[j]]]-2*F[j],p=fir[j]; if((F[A[i]]+F[A[fir[j]]]-2*F[j])<minx) minx=F[A[i]]+F[A[fir[j]]]-2*F[j],p=fir[j]; } else if(sec[j]) { if((F[A[i]]+F[A[sec[j]]]-2*F[j]==minx)&&(p>sec[j])) minx=F[A[i]]+F[A[sec[j]]]-2*F[j],p=sec[j]; if((F[A[i]]+F[A[sec[j]]]-2*F[j])<minx) minx=F[A[i]]+F[A[sec[j]]]-2*F[j],p=sec[j]; } } int jj=A[i]/j; if(jj==j) continue; if(fir[jj]) { if(fir[jj]!=i) { if((F[A[i]]+F[A[fir[jj]]]-2*F[jj]==minx)&&(p>fir[jj])) minx=F[A[i]]+F[A[fir[jj]]]-2*F[jj],p=fir[jj]; if((F[A[i]]+F[A[fir[jj]]]-2*F[jj])<minx) minx=F[A[i]]+F[A[fir[jj]]]-2*F[jj],p=fir[jj]; } else if(sec[jj]) { if((F[A[i]]+F[A[sec[jj]]]-2*F[jj]==minx)&&(p>sec[jj])) minx=F[A[i]]+F[A[sec[jj]]]-2*F[jj],p=sec[jj]; if((F[A[i]]+F[A[sec[jj]]]-2*F[jj])<minx) minx=F[A[i]]+F[A[sec[jj]]]-2*F[jj],p=sec[jj]; } } } } printf("%d ",p); } //cout<<(double)(clock())<<endl; return 0; }
| [Poi2012]Prefixuffix |
好题
一开始先是想sa暴力 然后被wph d了
然后想用exkmp和kmp再混搞 发现也很荒谬
wph说有性质 其实poi字符串的就没裸题有性质不出奇
性质一般是单调性的 这样可以降低复杂度
于是去别人家拜年的时候yy了一下性质
分界点每向右移一下 后面那段长度总会-1 当然你还移了一下 所以长度会-2
就是F[i]>=F[i-1]-2 虽然如此 还是不好做 打着打着发现
变换一下 F[i-1]<=F[i]+2 这样显然也会成立
然后就是hash了 一开始用exkmp 打了一半错了
http://blog.csdn.net/zsc2014030403015/article/details/51274118
写得挺好的 几乎就是按照里面说的hash
其中我觉得有点妙的地方就是
 View Code
View Code | [Poi2012]Festival |
这一题又让我脑补了差分约束..
一开始想把第二个条件缩点 然后第一个条件不没力了
后来看题解 .. 把第一个条件直接拆成两个条件搞(原来这样不会错)
然后直接差分缩联通快 跑最短路的最长路加起来就是了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<ext/rope> #include<cmath> #include<stack> #include<queue> using namespace std; const int Maxn=100010; int N,M1,M2; pair<int,int>A[Maxn],B[Maxn]; struct node { int x,y,next,d; }edge[Maxn*2]; int len,first[610]; void ins(int x,int y,int d) { len++; edge[len].x=x; edge[len].y=y; edge[len].d=d; edge[len].next=first[x]; first[x]=len; } // Spfa queue<int>Q; int Dis[610]; bool V[610]; int T[610]; bool Check() { len=0; memset(first,-1,sizeof(first)); int ST=0; for(int i=1;i<=M1;i++) ins(A[i].first,A[i].second,1),ins(A[i].second,A[i].first,-1); for(int i=1;i<=M2;i++) ins(B[i].second,B[i].first,0); for(int i=1;i<=N;i++) ins(ST,i,0); memset(T,0,sizeof(T)); while(!Q.empty()) Q.pop(); Q.push(ST); T[ST]++; memset(Dis,63,sizeof(Dis)); Dis[ST]=0; memset(V,0,sizeof(V)); V[ST]=1; while(!Q.empty()) { int x=Q.front(); if(T[x]==N+1) return false; for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(Dis[y]>Dis[x]+edge[k].d) { Dis[y]=Dis[x]+edge[k].d; if(!V[y]) { V[y]=1; T[y]++; Q.push(y); } } } V[x]=false; Q.pop(); }return true; } // Tarjan int low[610],dfn[610]; int id; stack<int>S; bool insta[610]; int belong[610]; int cnt; vector<int>Vec[610]; void Dfs(int x) { dfn[x]=low[x]=++id; insta[x]=1; S.push(x); for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(dfn[y]==-1) Dfs(y),low[x]=min(low[x],low[y]); else if(insta[y]) low[x]=min(low[x],dfn[y]); } if(dfn[x]==low[x]) { int i=S.top(); cnt++; do { i=S.top(); belong[i]=cnt; Vec[cnt].push_back(i); insta[i]=false; S.pop(); }while(i!=x); } } int F[610][610]; int main() { scanf("%d%d%d",&N,&M1,&M2); for(int i=1;i<=M1;i++) scanf("%d%d",&A[i].first,&A[i].second); for(int i=1;i<=M2;i++) scanf("%d%d",&B[i].first,&B[i].second); if(Check()) { len=0; memset(first,-1,sizeof(first)); for(int i=1;i<=M1;i++) ins(A[i].first,A[i].second,1),ins(A[i].second,A[i].first,-1); for(int i=1;i<=M2;i++) ins(B[i].second,B[i].first,0); memset(dfn,-1,sizeof(dfn)); memset(low,-1,sizeof(low)); memset(insta,0,sizeof(insta)); id=0; for(int i=1;i<=N;i++) if(dfn[i]==-1) Dfs(i); memset(F,63,sizeof(F)); for(int i=1;i<=M1;i++) F[A[i].first][A[i].second]=min(F[A[i].first][A[i].second],1),F[A[i].second][A[i].first]=min(F[A[i].second][A[i].first],-1); for(int i=1;i<=M2;i++) F[B[i].second][B[i].first]=min(F[B[i].second][B[i].first],0); for(int k=1;k<=N;k++) for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) F[i][j]=min(F[i][j],F[i][k]+F[k][j]); int ans=0; for(int i=1;i<=cnt;i++) { int maxx=0; for(int x=0;x<Vec[i].size();x++) for(int y=0;y<Vec[i].size();y++) if(F[Vec[i][x]][Vec[i][y]]<99999999) maxx=max(maxx,F[Vec[i][x]][Vec[i][y]]); ans+=maxx+1; } printf("%d ",ans); } else printf("NIE "); return 0; }
| [Tjoi2016&Heoi2016]树 |
树剖/并查集

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=100010; struct node { int x,y,next; }edge[Maxn]; int len,first[Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } int N,M; int root; int dep[Maxn]; int fa[Maxn],dfn[Maxn],z,Hash[Maxn]; int size[Maxn],son[Maxn]; int top[Maxn]; void Dfs(int x) { size[x]=1; son[x]=0; for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; fa[y]=x; dep[y]=dep[x]+1; Dfs(y); size[x]+=size[y]; if(size[y]>size[son[x]]) son[x]=y; } } void Dfs2(int x,int tp) { top[x]=tp; dfn[x]=++z; Hash[z]=x; if(son[x]) Dfs2(son[x],tp); for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(y!=son[x]) Dfs2(y,y); } } int rt,lc[Maxn*4],rc[Maxn*4]; int tot; int C[Maxn*4]; void Link(int &u,int L,int R,int k) { if(!u) u=++tot; if(L==R) return ; int mid=(L+R)>>1; if(k<=mid) Link(lc[u],L,mid,k); else Link(rc[u],mid+1,R,k); } void Change(int u,int L,int R,int k) { if(L==R){C[u]=L; return ;} int mid=(L+R)>>1; if(k<=mid) Change(lc[u],L,mid,k); else Change(rc[u],mid+1,R,k); C[u]=max(C[lc[u]],C[rc[u]]); } int Query(int u,int L,int R,int l,int r) { if(C[u]==0) return 0; if(L==l&&R==r) return C[u]; int mid=(L+R)>>1; if(r<=mid) return Query(lc[u],L,mid,l,r); else if(l>mid) return Query(rc[u],mid+1,R,l,r); else return max(Query(lc[u],L,mid,l,mid),Query(rc[u],mid+1,R,mid+1,r)); } int Q(int x) { int tx=top[x]; while(1) { int ans=Query(rt,1,z,dfn[tx],dfn[x]); if(ans==0) x=fa[tx],tx=top[x]; else return Hash[ans]; } } int main() { scanf("%d%d",&N,&M); len=0; memset(first,-1,sizeof(first)); for(int i=1;i<N;i++) { int x,y; scanf("%d%d",&x,&y); ins(x,y); }root=1; z=0; memset(dep,0,sizeof(dep)); dep[root]=1; Dfs(root); Dfs2(root,root); tot=0; for(int i=1;i<=z;i++) Link(rt,1,z,i); memset(C,0,sizeof(C)); Change(rt,1,z,dfn[1]); for(int i=1;i<=M;i++) { char st; scanf(" %c",&st); int x; scanf("%d",&x); if(st=='C') Change(rt,1,z,dfn[x]); else if(st=='Q') printf("%d ",Q(x)); } return 0; } /* 5 5 1 2 1 3 2 4 2 5 Q 2 C 2 Q 2 Q 5 Q 3 */
| [Tjoi2016&Heoi2016]排序 |
太垃圾了不会做
以后不会做想想二分这个位置的数
大于的1 小于-1 等于 0 然后每个询问线段树只管大小 然后yy了一下写了4K调了一下ac了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=100010; struct node { int opt,l,r; }Q[Maxn]; int N,M; int A[Maxn]; int pos; int lc[Maxn*4],rc[Maxn*4],B[Maxn*4],E[Maxn*4],S[Maxn*4],lazy[Maxn*4]; bool bk[Maxn*4]; int P[Maxn*4]; int root,tot; //B Bigger E Equal L Less //P -2 mix void Update(int u) { B[u]=B[lc[u]]+B[rc[u]]; E[u]=E[lc[u]]+E[rc[u]]; S[u]=S[lc[u]]+S[rc[u]]; if(bk[lc[u]]&&bk[rc[u]]&&P[lc[u]]==P[rc[u]]) { P[u]=P[lc[u]]; bk[u]=1; } else bk[u]=0,P[u]=-2; } void Push_down(int u,int L,int R) { if(lazy[u]!=-2) { int mid=(L+R)>>1; if(lazy[u]==-1) S[lc[u]]=mid-L+1,B[lc[u]]=E[lc[u]]=0; if(lazy[u]==0) E[lc[u]]=mid-L+1,B[lc[u]]=S[lc[u]]=0; if(lazy[u]==1) B[lc[u]]=mid-L+1,S[lc[u]]=E[lc[u]]=0; bk[lc[u]]=1; lazy[lc[u]]=lazy[u]; P[lc[u]]=lazy[u]; if(lazy[u]==-1) S[rc[u]]=R-mid,B[rc[u]]=E[rc[u]]=0; if(lazy[u]==0) E[rc[u]]=R-mid,B[rc[u]]=S[rc[u]]=0; if(lazy[u]==1) B[rc[u]]=R-mid,S[rc[u]]=E[rc[u]]=0; bk[rc[u]]=1; lazy[rc[u]]=lazy[u]; P[rc[u]]=lazy[u]; lazy[u]=-2; } } void Link(int &u,int L,int R,int k,int b,int e,int s) { if(!u){u=++tot; lazy[u]=-2;} if(L==R) { B[u]=b; E[u]=e; S[u]=s; bk[u]=1; if(B[u]) P[u]=1; if(E[u]) P[u]=0; if(S[u]) P[u]=-1; return ; } int mid=(L+R)>>1; if(k<=mid) Link(lc[u],L,mid,k,b,e,s); else Link(rc[u],mid+1,R,k,b,e,s); Update(u); } int Bs,Ss,Es; void Query(int u,int L,int R,int l,int r) { if(L==l&&R==r) { Bs+=B[u]; Ss+=S[u]; Es+=E[u]; return ; } Push_down(u,L,R); int mid=(L+R)>>1; if(r<=mid) Query(lc[u],L,mid,l,r); else if(l>mid) Query(rc[u],mid+1,R,l,r); else { Query(lc[u],L,mid,l,mid); Query(rc[u],mid+1,R,mid+1,r); } } void Change(int u,int L,int R,int l,int r,int c) { if(l>r) return ; if(L==l&&R==r) { if(c==-1) S[u]=R-L+1,B[u]=E[u]=0; if(c==0) E[u]=R-L+1,B[u]=S[u]=0; if(c==1) B[u]=R-L+1,S[u]=E[u]=0; bk[u]=1; lazy[u]=c; P[u]=c; return ; } int mid=(L+R)>>1; Push_down(u,L,R); if(r<=mid) Change(lc[u],L,mid,l,r,c); else if(l>mid) Change(rc[u],mid+1,R,l,r,c); else { Change(lc[u],L,mid,l,mid,c); Change(rc[u],mid+1,R,mid+1,r,c); } Update(u); } int Check(int x) { tot=root=0; memset(lc,0,sizeof(lc)); memset(rc,0,sizeof(rc)); for(int i=1;i<=N;i++) { if(A[i]<x) Link(root,1,N,i,0,0,1); if(A[i]==x) Link(root,1,N,i,0,1,0); if(A[i]>x) Link(root,1,N,i,1,0,0); } for(int i=1;i<=M;i++) { Bs=Ss=Es=0; Query(root,1,N,Q[i].l,Q[i].r); if(Q[i].opt==0) { Change(root,1,N,Q[i].l,Q[i].l+Ss-1,-1); Change(root,1,N,Q[i].l+Ss,Q[i].l+Ss+Es-1,0); Change(root,1,N,Q[i].l+Ss+Es,Q[i].l+Ss+Es+Bs-1,1); } else if(Q[i].opt==1) { Change(root,1,N,Q[i].l,Q[i].l+Bs-1,1); Change(root,1,N,Q[i].l+Bs,Q[i].l+Bs+Es-1,0); Change(root,1,N,Q[i].l+Bs+Es,Q[i].l+Ss+Bs+Es-1,-1); } } Bs=Ss=Es=0; Query(root,1,N,pos,pos); if(Bs) return 1; if(Ss) return -1; if(Es) return 0; } int main() { scanf("%d%d",&N,&M); for(int i=1;i<=N;i++) scanf("%d",&A[i]); for(int i=1;i<=M;i++) scanf("%d%d%d",&Q[i].opt,&Q[i].l,&Q[i].r); scanf("%d",&pos); int L=1; int R=N; int ret=-1; while(L<=R) { int mid=(L+R)>>1; int od=Check(mid); if(od==0){printf("%d ",mid); break;} else if(od==-1) R=mid-1; else L=mid+1; } return 0; } /* 6 3 1 6 2 5 3 4 0 1 4 1 3 6 0 2 4 3 */
| [Tjoi2016&Heoi2016]字符串 |
O(NM) 最开始想的
一般这些题感觉还会有更快的 比如两个log 然后想咯
首先二分长度 然后发现在那个rank的表上可以找到公共前缀为长度的
也是用二分 然后用主席树判断在不在a..b中

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=100010; int N,M,A[Maxn]; int L[Maxn],R[Maxn]; int F[Maxn]; int B[Maxn]; bool Cmp1(int x,int y){return A[x]<A[y];} bool Cmp2(int x,int y){return L[x]<L[y];} int tr[Maxn]; int low_bit(int x){return x&(-x);} void Add(int x,int c){for(int i=x;i<=100000;i+=low_bit(i)) tr[i]=max(tr[i],c);} int Query(int x){int maxx=0; for(int i=x;i>=1;i-=low_bit(i)) maxx=max(tr[i],maxx); return maxx;} void CDQ(int l,int r) { if(l==r){F[l]=max(F[l],1); return ;} int mid=(l+r)>>1; CDQ(l,mid); for(int i=l;i<=r;i++) B[i]=i; sort(B+l,B+mid+1,Cmp1); sort(B+mid+1,B+r+1,Cmp2); int i=l; for(int j=mid+1;j<=r;j++) { while(i<=mid&&A[B[i]]<=L[B[j]]) Add(R[B[i]],F[B[i]]),i++; F[B[j]]=max(F[B[j]],Query(A[B[j]])+1); } for(int i=l;i<=r;i++) for(int j=R[i];j<=100000;j+=low_bit(j)) tr[j]=0; CDQ(mid+1,r); } int main() { scanf("%d%d",&N,&M); for(int i=1;i<=N;i++) scanf("%d",&A[i]),L[i]=R[i]=A[i]; for(int i=1;i<=M;i++) { int pos,x; scanf("%d%d",&pos,&x); L[pos]=min(L[pos],x); R[pos]=max(R[pos],x); } memset(tr,0,sizeof(tr)); CDQ(1,N); int maxx=0; for(int i=1;i<=N;i++) maxx=max(maxx,F[i]); return printf("%d ",maxx),0; }
| [Tjoi2016&Heoi2016]游戏 |
简单的二分匹配 行标号 列标号 然后连线

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=51; struct node { int x,y,next; }edge[Maxn*Maxn]; int len,first[Maxn*Maxn]; void ins(int x,int y) { len++; edge[len].x=x; edge[len].y=y; edge[len].next=first[x]; first[x]=len; } int N,M; char st[Maxn][Maxn]; int R[Maxn][Maxn],C[Maxn][Maxn]; int r,c; bool chw[Maxn*Maxn]; int match[Maxn*Maxn]; bool Find(int x) { for(int k=first[x];k!=-1;k=edge[k].next) { int y=edge[k].y; if(chw[y]) { chw[y]=0; if(match[y]==0||Find(match[y])){match[y]=x; return 1;} } } return 0; } int main() { scanf("%d%d",&N,&M); len=0; memset(first,-1,sizeof(first)); for(int i=1;i<=N;i++) for(int j=1;j<=M;j++) scanf(" %c",&st[i][j]); r=0; c=0; for(int i=1;i<=N;i++) st[i][0]='#'; for(int i=1;i<=N;i++) { for(int j=1;j<=M;j++) { if(st[i][j]=='#') continue; if(st[i][j-1]=='#') r++; R[i][j]=r; } } for(int i=1;i<=M;i++) st[0][i]='#'; for(int j=1;j<=M;j++) { for(int i=1;i<=N;i++) { if(st[i][j]=='#') continue; if(st[i-1][j]=='#') c++; C[i][j]=c; } } for(int i=1;i<=N;i++) for(int j=1;j<=M;j++) { if(st[i][j]=='#'||st[i][j]=='x') continue; ins(R[i][j],C[i][j]); } int ans=0; memset(match,0,sizeof(match)); for(int i=1;i<=r;i++) { memset(chw,1,sizeof(chw)); if(Find(i)) ans++; } return printf("%d ",ans),0; } /* 4 4 #*** *#** **#* xxx# */
| [Tjoi2016&Heoi2016]序列 |
假设一个数变化到最大的可以是R[i] 变化到最小的可以是L[i] 可以影响前面必须要满足
i<j A[i]<=L[j] A[j]>=R[i] -> F[j]=max(F[i]+1)
三个变量 随便用CDQ写写就好

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=100010; int N,M,A[Maxn]; int L[Maxn],R[Maxn]; int F[Maxn]; int B[Maxn]; bool Cmp1(int x,int y){return A[x]<A[y];} bool Cmp2(int x,int y){return L[x]<L[y];} int tr[Maxn]; int low_bit(int x){return x&(-x);} void Add(int x,int c){for(int i=x;i<=100000;i+=low_bit(i)) tr[i]=max(tr[i],c);} int Query(int x){int maxx=0; for(int i=x;i>=1;i-=low_bit(i)) maxx=max(tr[i],maxx); return maxx;} void CDQ(int l,int r) { if(l==r){F[l]=max(F[l],1); return ;} int mid=(l+r)>>1; CDQ(l,mid); for(int i=l;i<=r;i++) B[i]=i; sort(B+l,B+mid+1,Cmp1); sort(B+mid+1,B+r+1,Cmp2); int i=l; for(int j=mid+1;j<=r;j++) { while(i<=mid&&A[B[i]]<=L[B[j]]) Add(R[B[i]],F[B[i]]),i++; F[B[j]]=max(F[B[j]],Query(A[B[j]])+1); } for(int i=l;i<=r;i++) for(int j=R[i];j<=100000;j+=low_bit(j)) tr[j]=0; CDQ(mid+1,r); } int main() { scanf("%d%d",&N,&M); for(int i=1;i<=N;i++) scanf("%d",&A[i]),L[i]=R[i]=A[i]; for(int i=1;i<=M;i++) { int pos,x; scanf("%d%d",&pos,&x); L[pos]=min(L[pos],x); R[pos]=max(R[pos],x); } memset(tr,0,sizeof(tr)); CDQ(1,N); int maxx=0; for(int i=1;i<=N;i++) maxx=max(maxx,F[i]); return printf("%d ",maxx),0; }
| [Ahoi2009]chess 中国象棋 |
我好菜鸡啊 膜硕爷
发现炮的话 每行每列也就放2个最多
然后dp行 放0个和放1个的列有多少列 发现列是等价的

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Mod=9999973; const LL Maxn=110; LL N,M; LL F[Maxn][Maxn][Maxn]; int main() { scanf("%lld%lld",&N,&M); memset(F,0,sizeof(F)); F[0][M][0]=1; for(LL i=1;i<=N;i++) { for(LL j=0;j<=M;j++) { for(LL k=0;k<=M;k++) { F[i][j][k]=(F[i][j][k]+F[i-1][j][k])%Mod; F[i][j][k]=(F[i][j][k]+F[i-1][j+1][k-1]*(j+1))%Mod; F[i][j][k]=(F[i][j][k]+F[i-1][j][k+1]*(k+1))%Mod; F[i][j][k]=(F[i][j][k]+F[i-1][j+2][k-2]*(j+1)*(j+2)/2)%Mod; F[i][j][k]=(F[i][j][k]+F[i-1][j+1][k]*(j+1)*k)%Mod; F[i][j][k]=(F[i][j][k]+F[i-1][j][k+2]*(k+1)*(k+2)/2)%Mod; } } } LL ans=0; for(LL i=0;i<=M;i++) for(LL j=0;j<=M;j++) ans=(ans+F[N][i][j])%Mod; return printf("%lld ",ans),0; }
| [Ahoi2005]COMMON 约数研究 |
换思维枚举约数

#include<cstdio> #include<iostream> using namespace std; int main() { int N,ans; scanf("%d",&N); ans=0; for(int i=1;i<=N;i++) ans+=N/i; printf("%d ",ans); return 0; }
| mode |
一个个数抵消好题

#include<cstdio> using namespace std; int N,p=0,x,tot=0; int main() { scanf("%d",&N); while(N--) { scanf("%d",&x); if(!tot) p=x,tot=1; else if(x!=p) tot--; else if(x==p) tot++; } return printf("%d ",p),0; }
| [Ahoi2009]Seq 维护序列seq |
线段树 想想分配律?

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; typedef long long LL; const LL Maxn=410000; LL lc[Maxn*4]; LL rc[Maxn*4]; LL C[Maxn*4]; LL A[Maxn*4]; LL M[Maxn*4]; LL root,tot; LL N,P; void Link(LL &u,LL L,LL R,LL k,LL c) { if(!u) u=++tot; if(L==R){M[u]=1; A[u]=0; C[u]=c; return ;} LL mid=(L+R)>>1; if(k<=mid) Link(lc[u],L,mid,k,c); else Link(rc[u],mid+1,R,k,c); C[u]=(C[lc[u]]+C[rc[u]])%P; M[u]=1; A[u]=0; } void Push_down(LL u,LL L,LL R) { LL mid=(L+R)>>1; M[lc[u]]=(M[lc[u]]*M[u])%P; M[rc[u]]=(M[rc[u]]*M[u])%P; A[lc[u]]=(A[lc[u]]*M[u]+A[u])%P; A[rc[u]]=(A[rc[u]]*M[u]+A[u])%P; C[lc[u]]=(C[lc[u]]*M[u]+A[u]*(mid-L+1))%P; C[rc[u]]=(C[rc[u]]*M[u]+A[u]*(R-mid))%P; M[u]=1; A[u]=0; } void Mul(LL u,LL L,LL R,LL l,LL r,LL c) { if(L==l&&R==r){M[u]=(M[u]*c)%P; A[u]=(A[u]*c)%P; C[u]=(C[u]*c)%P; return ;} Push_down(u,L,R); LL mid=(L+R)>>1; if(r<=mid) Mul(lc[u],L,mid,l,r,c); else if(l>mid) Mul(rc[u],mid+1,R,l,r,c); else { Mul(lc[u],L,mid,l,mid,c); Mul(rc[u],mid+1,R,mid+1,r,c); } C[u]=(C[lc[u]]+C[rc[u]])%P; } void Add(LL u,LL L,LL R,LL l,LL r,LL c) { if(L==l&&R==r){A[u]=(A[u]+c)%P; C[u]=(C[u]+c*(R-L+1))%P; return ;} Push_down(u,L,R); LL mid=(L+R)>>1; if(r<=mid) Add(lc[u],L,mid,l,r,c); else if(l>mid) Add(rc[u],mid+1,R,l,r,c); else { Add(lc[u],L,mid,l,mid,c); Add(rc[u],mid+1,R,mid+1,r,c); } C[u]=(C[lc[u]]+C[rc[u]])%P; } LL Query(LL u,LL L,LL R,LL l,LL r) { if(L==l&&R==r) return C[u]; Push_down(u,L,R); LL mid=(L+R)>>1; if(r<=mid) return Query(lc[u],L,mid,l,r); else if(l>mid) return Query(rc[u],mid+1,R,l,r); else return (Query(lc[u],L,mid,l,mid)+Query(rc[u],mid+1,R,mid+1,r))%P; } int main() { scanf("%lld%lld",&N,&P); root=tot=0; for(LL i=1;i<=N;i++) { LL x; scanf("%lld",&x); Link(root,1,N,i,x); } LL M; scanf("%lld",&M); for(LL i=1;i<=M;i++) { LL opt,L,R,c; scanf("%lld%lld%lld",&opt,&L,&R); if(opt==3) printf("%lld ",Query(root,1,N,L,R)); else { scanf("%lld",&c); if(opt==1) Mul(root,1,N,L,R,c); else Add(root,1,N,L,R,c); } } return 0; }
| [Ahoi2009]fly 飞行棋 |
发现四条边两对对边分别相等就行了

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> using namespace std; const int Maxn=30; int A[Maxn]; int Sum[Maxn]; int N; int C[Maxn]; bool V[Maxn]; int ans=0; void Dfs(int K) { if(K==5) { int a,b,c,d; a=Sum[C[2]]-Sum[C[1]]; b=Sum[C[3]]-Sum[C[2]]; c=Sum[C[4]]-Sum[C[3]]; d=Sum[N]-Sum[C[4]]+Sum[C[1]]; if(a==c&&b==d) { //printf("%d %d %d %d ",C[1],C[2],C[3],C[4]); ans++; return ; } } else { for(int i=C[K-1]+1;i<=N;i++) { if(V[i]) { C[K]=i; V[i]=false; Dfs(K+1); V[i]=true; } } } } int main() { scanf("%d",&N); for(int i=1;i<=N;i++) scanf("%d",&A[i]); for(int i=1;i<=N;i++) Sum[i]=Sum[i-1]+A[i]; memset(V,1,sizeof(V)); Dfs(1); return printf("%d ",ans),0; }
| [Ahoi2013]差异 |
好题啊啊被我想出来了哈哈哈哈
首先我们求出height之后 问题就变成了sigma(min(height[i]...height[j-1],height[j]))
然后枚举height 用set搞 搞完一个插一个就行 时间Nlogn

#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<cmath> #include<cstdlib> #include<vector> #include<set> using namespace std; typedef long long LL; const LL Maxn=500010; char str[Maxn]; LL A[Maxn]; LL N; LL rank[Maxn],sa[Maxn],R[Maxn],fir[Maxn],sec[Maxn],height[Maxn]; void Rsort(LL *use,LL *in,LL *out,LL num,LL size) { for(LL i=1;i<=size;i++) R[i]=0; for(LL i=1;i<=num;i++) R[use[in[i]]]++; for(LL i=1;i<=size;i++) R[i]+=R[i-1]; for(LL i=num;i>=1;i--) out[R[use[in[i]]]--]=in[i]; } void SA() { for(LL i=1;i<=N;i++) rank[i]=i; Rsort(A,rank,sa,N,300); rank[sa[1]]=1; for(LL i=2;i<=N;i++) rank[sa[i]]=rank[sa[i-1]]+(A[sa[i-1]]!=A[sa[i]]); LL p=0; LL cnt=1; while(cnt<N) { for(LL i=1;i<=N;i++) { fir[i]=rank[i]; sec[i]=(i+(1<<p))>N?0:rank[i+(1<<p)]; sa[i]=i; } Rsort(sec,sa,rank,N,N); Rsort(fir,rank,sa,N,N); rank[sa[1]]=1; for(LL i=2;i<=N;i++) rank[sa[i]]=rank[sa[i-1]]+((fir[sa[i-1]]!=fir[sa[i]])||(sec[sa[i-1]]!=sec[sa[i]])); cnt=rank[sa[N]]; p++; } } void Height() { LL k=0; for(LL i=1;i<=N;i++) { if(k) k--; if(rank[i]!=1) { LL pos=sa[rank[i]-1]; while(A[pos+k]==A[i+k]) k++; } height[rank[i]]=k; } } vector<LL>V[Maxn]; set<LL>S; set<LL>::iterator it1,it2; int main() { gets(str+1); N=strlen(str+1); for(LL i=1;i<=N;i++) A[i]=str[i]; SA(); Height(); LL ans=(N-1)*(N+1)*N/2; for(LL i=2;i<=N;i++) V[height[i]].push_back(i-1); for(LL i=0;i<=N;i++) sort(V[i].begin(),V[i].end()); S.clear(); S.insert(0); S.insert(N); for(LL i=0;i<=N;i++) { for(LL j=0;j<V[i].size();j++) { LL k=V[i][j]; LL s=1; it1=S.lower_bound(V[i][j]); s=(*it1)-V[i][j]; it1--; s*=V[i][j]-(*it1); ans-=i*s*2; S.insert(V[i][j]); } } return printf("%lld ",ans),0; }
