https://vjudge.net/problem/UVA-815原题连接,图片来源https://blog.csdn.net/ZscDst/article/details/80342588,https://blog.csdn.net/code4101/article/details/38540759若有侵权,我马上删。
刘佳汝书第四章练习的最后一道。这题开始的时候死活看不懂题是什么意思,直到查了许多分析才明白这题让干嘛。
结果被些许分析形成了部分先入为主的思路,没能完全独立思考,有点可惜,所以,如果你只是看不懂题的话,请看这里:
给你一个n*m的矩阵输入,矩阵中的每个值可以看作一个n*m个立体方格的每个位置上的海拔高度(可以有负值),每个方格底面均为10m*10m。
现在有洪水天降,第二行输入一个洪水的体积,这个n*m的区域四面为无限高的墙壁,洪水只会在这个n*m的区域,也不会渗入到土里,不流失,不蒸发。
这是一组完整输入,不停读入知道读入n,m为0 ,0。
判断并按格式输出每组最终的水面高度和有百分之多少的格子完全被淹没在水面之下了,具体要求看题。
一图胜千言,上图!
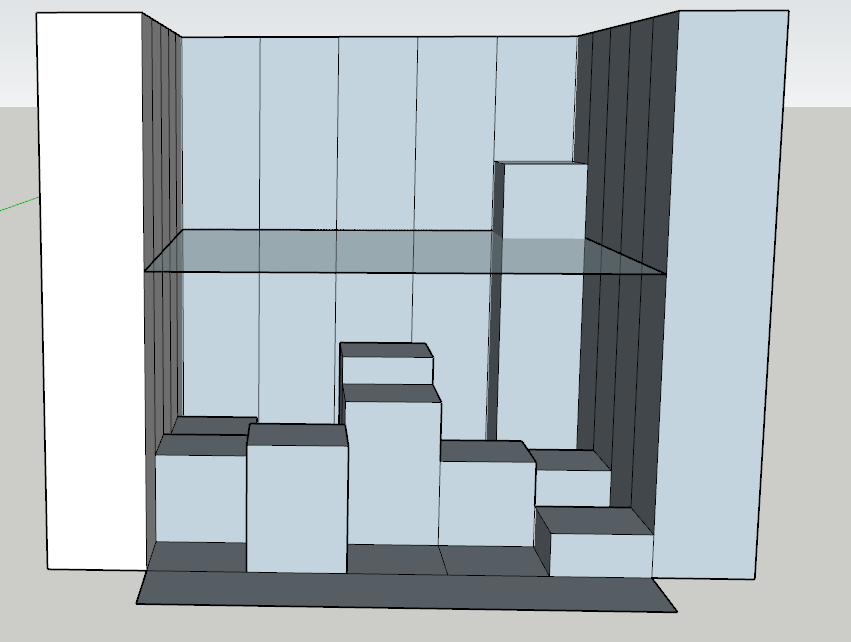

感谢网上那个会建模的大神做的图片,这样一看就清楚了。这些格子要理解为并不是彼此间封死的,水一定有办法流到最低的格子。
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
下面题解:
受这位自称只会做水题的学姐的思路启发。https://www.cnblogs.com/mofushaohua/p/7789471.html
水会依次填满海拔最低的格子,所谓“填满”也就是说因为它比其他格子海拔都低,四周就把他围成个洞一样。
所以若将输入的水的体积/100(固定底面积)之后,并且按升序排列所以格子高度,就可以将问题想为用固定高度的水依次拉满不同高度的水平面h[n+1]=h水+h[n]原,三维变二维。
然后要注意每次拉高当前最低格子睡眠后,下一次要填的格子+1,想一下从拉高第一个最矮格子的水平面后,它就与倒数第二并列最矮了,所以下次要拉的数量就是两个。
循环此过程直到剩下的水不够将水面拉到第n次的格子。而水面永远是平的,所以最终海拔面就是 (h水总高度+h[1]……+h[n-1])/(n-1)并且 n-1/格子总数 就为淹没百分比。
想明白其实就是,真*水题;
没用解除流绑定,我自己的。
#include<iostream> #include<algorithm> #include<string> #include<iomanip> #define N 1000 #define inf 0x3f3f3f3f using namespace std; int h[N]; int main() { int n, m,cnt=1; while (cin >> n >> m && n&&m) { n *= m; memset(h, 0, sizeof(h)); for (int i = 0; i < n; i++) cin >> h[i]; double sum = 0; cin >> sum; sum /= 100; sort(h, h + n); h[n] = inf; int i; for ( i = 0; i < n; i++) { sum += h[i]; if (sum / (i + 1) <= h[i + 1]) break; } cout << "Region " << cnt++ << endl; cout << "Water level is " <<fixed<<setprecision(2)<<sum/(i+1)<< " meters." << endl; cout << (i+1)*100.00/n<< " percent of the region is under water." << endl << endl; } return 0; }
//用了解除流绑定,水题学姐的
#include <iostream> #include <algorithm> #include<iomanip> using namespace std; const int N = 1000; const int INF = 0x3f3f3f3f; int h[N]; // height int main() { cin.tie(0); cin.sync_with_stdio(false); int kase = 0; int n, m; while (cin >> n >> m && n && m) { n *= m; for (int i = 0; i < n; i++) cin >> h[i]; sort(h, h + n); //将海拔高度从小到大排序 h[n] = INF; int k; double sum; cin >> sum; sum /= 100.0; //体积除以底面积,得到洪水真正的高度 for (k = 1; k <= n; k++) { sum += h[k - 1]; //将洪水高度与 单个格子高度 相加。 if (sum / k < h[k]) break; // 计算当前格子前面的格子的海拔高度,若小于当前格子的高度,说明当前格子一定不会被装满水,可以退出 // 为了处理边界情况,因此将a[n]设置为一个无穷大的数,使得若是所有格子都能装满,仍然可以用此循环正确退出,并得到正确的结果 } cout << "Region " << ++kase << endl; cout << "Water level is " << fixed << setprecision(2) << 1.0 * sum / k << " meters." << endl; cout << k * 100.0 / n << " percent of the region is under water." << endl << endl; } return 0; }
另外用不用io流绑定速度影响输入输出速度,能查个几十倍你敢信?0ms 和10 ms这个倍数可能对于某些题就runtime limit error了。
