作为一个非理工科的经管学生,在数学基础有限的情况的,理解难免不足。文章多有copy。
参考博客:
https://blog.csdn.net/zouxy09/article/details/24971995
1.前言
为什么探讨L0,L1,L2范数,机器学习中出现的非常频繁的问题:过拟合与规则化。
机器学习的问题是“minimize your error while regularizing your parameters”。规则化参数的同时最小化误差。最小化误差是为了让模型拟合我们的训练数据,而规则化参数是防止我们的模型过分拟合我们的训练数据。
因为参数太多,会导致我们的模型复杂度上升,容易过拟合,也就是我们的训练误差会很小。但训练误差小并不是我们的最终目标,我们的目标是希望模型的测试误差小,也就是能准确的预测新的样本。
所以,我们需要保证模型“简单”的基础上最小化训练误差,这样得到的参数才具有好的泛化性能(也就是测试误差也小),而模型“简单”就是通过规则函数来实现的。另外,规则项的使用还可以约束我们的模型的特性。
这样就可以将人对这个模型的先验知识融入到模型的学习当中,强行地让学习到的模型具有人想要的特性,例如稀疏、低秩、平滑等等。
有时候人的先验是非常重要的,好的先验肯定能使机器更快的学习相应的任务。人和机器的交流目前还没有那么直接的方法,这个媒介只能由规则项来担当。
其他角度来看待规则化的。规则化符合奥卡姆剃刀(Occam's razor)原理。它的思想是:在所有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。
从贝叶斯估计的角度来看,规则化项对应于模型的先验概率。规则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或惩罚项(penalty term)。
监督学习可以看做最小化下面的目标函数:

其中,第一项L(yi,f(xi;w)) 衡量我们的模型(分类或者回归)对第i个样本的预测值f(xi;w)和真实的标签yi之前的误差。
因为我们的模型是要拟合我们的训练样本的嘛,所以我们要求这一项最小,也就是要求我们的模型尽量的拟合我们的训练数据。
但正如上面说言,我们不仅要保证训练误差最小,我们更希望我们的模型测试误差小,所以我们需要加上第二项,也就是对参数w的规则化函数Ω(w)去约束我们的模型尽量的简单。
机器学习的大部分带参模型都和这个相似。其实大部分无非就是变换这两项而已。
对于第一项Loss函数,如果是Square loss,那就是最小二乘了;
如果是Hinge Loss,那就是著名的SVM了;
如果是exp-Loss,那就是 Boosting了;
如果是log-Loss,那就是Logistic Regression了;
还有等等。不同的loss函数,具有不同的拟合特性,这个也得就具体问题具体分析的。
但这里,我们先不究loss函数的问题,我们把目光转向“规则项Ω(w)”。
规则化函数Ω(w)也有很多种选择,一般是模型复杂度的单调递增函数,模型越复杂,规则化值就越大。比如,规则化项可以是模型参数向量的范数。
然而,不同的选择对参数w的约束不同,取得的效果也不同,但我们在论文中常见的都聚集在:零范数、一范数、二范数、迹范数、Frobenius范数和核范数等等。
2.L0范数与L1范数
L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0,让参数W是稀疏的。
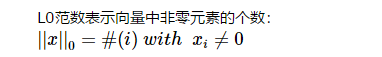
“压缩感知”和“稀疏编码”都用到了参数稀疏,“稀疏”就是通过这类范数实现的。但是是这样吗?看到大多数的papers中,稀疏不是都通过L1范数来实现吗,更多用到的都是||W||1!
下面把L0和L1放在一起的原因,因为他们有着某种不寻常的关系。那我们再来看看L1范数是什么?它为什么可以实现稀疏?为什么大家都用L1范数去实现稀疏,而不是L0范数呢?
L1范数是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。
为什么L1范数会使权值稀疏?有人可能会这样给你回答“它是L0范数的最优凸近似”。
回答:任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。这说是这么说,W的L1范数是绝对值,|w|在w=0处是不可微,但这还是不够直观。
但不幸的是,L0范数的最优化问题是一个NP hard问题,而且理论上有证明,L1范数是L0范数的最优凸近似,因此通常使用L1范数来代替。

L1可以实现稀疏,但是为什么要稀疏?让我们的参数稀疏有什么好处呢?
为了:
1)特征选择(Feature Selection):
选择稀疏规则一个关键原因在于它能实现特征的自动选择。一般来说,xi的大部分元素(也就是特征)都是和最终的输出yi没有关系或者不提供任何信息的,在最小化目标函数的时候考虑xi这些额外的特征,虽然可以获得更小的训练误差,但在预测新的样本时,这些没用的信息反而会被考虑,从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。
2)可解释性(Interpretability):
另一个青睐于稀疏的理由是,模型更容易解释。例如患某种病的概率是y,然后我们收集到的数据x是1000维的,也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型:y=w1*x1+w2*x2+…+w1000*x1000+b(当然了,为了让y限定在[0,1]的范围,一般还得加个Logistic函数)。通过学习,如果最后学习到的w*就只有很少的非零元素,例如只有5个非零的wi,那么我们就有理由相信,这些对应的特征在患病分析上面提供的信息是巨大的,决策性的。也就是说,患不患这种病只和这5个因素有关,那医生就好分析多了。但如果1000个wi都非0,医生面对这1000种因素,难以做出分析。
3.L2范数
除了L1范数,还有一种更受宠幸的规则化范数是L2范数: ||W||2。它也不逊于L1范数,它有两个美称,在回归里面,有人把有它的回归叫“岭回归”(Ridge Regression),有人也叫它“权值衰减weight decay”。
这用的很多吧,因为它的强大功效是改善机器学习里面一个非常重要的问题:过拟合。过拟合,就是模型训练时候的误差很小,但在测试的时候误差很大,也就是我们的模型复杂到可以拟合到我们的所有训练样本了,但在实际预测新的样本的时候,糟糕的一塌糊涂。

为什么L2范数可以防止过拟合?回答这个问题之前,我们得先看看L2范数是个什么东西。
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项||W||2最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0,这里是有很大的区别的哦。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单?我也不懂,我的理解是:限制了参数很小,实际上就限制了多项式某些分量的影响很小(看上面线性回归的模型的那个拟合的图),这样就相当于减少参数个数。
代码实现:
# 根据l2公式定义函数 def l2_normalize(v, axis=-1, order=2): l2 = np.linalg.norm(v, ord = order, axis=axis, keepdims=True) l2[l2==0] = 1 return v/l2 # 生成随机数据 Z = np.random.randint(10, size=(5,5)) print(Z) l2_normalize(Z)

L2范数的好处是什么呢?这里也扯上两点:
1)学习理论的角度:
从学习理论的角度来说,L2范数可以防止过拟合,提升模型的泛化能力。
2)优化计算的角度:
从优化或者数值计算的角度来说,L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。这condition number是啥?这涉及到优化问题。优化有两大难题,一是:局部最小值,二是:ill-condition病态问题。前者是,我们要找的是全局最小值,如果局部最小值太多,那我们的优化算法就很容易陷入局部最小而不能自拔,ill-condition对应的是well-condition。那他们分别代表什么?假设我们有个方程组AX=b,我们需要求解X。如果A或者b稍微的改变,会使得X的解发生很大的改变,那么这个方程组系统就是ill-condition的,反之就是well-condition的。
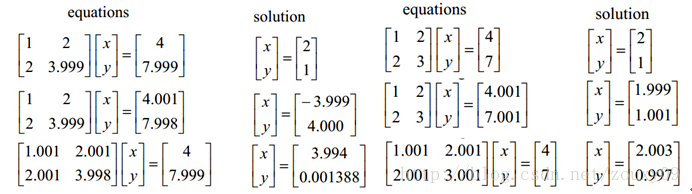
左边:第一行假设是我们的AX=b,第二行我们稍微改变下b,得到的x和没改变前的差别很大,看到吧。第三行我们稍微改变下系数矩阵A,可以看到结果的变化也很大。换句话来说,这个系统的解对系数矩阵A或者b太敏感了。又因为一般我们的系数矩阵A和b是从实验数据里面估计得到的,所以它是存在误差的,如果我们的系统对这个误差是可以容忍的就还好,但系统对这个误差太敏感了,以至于我们的解的误差更大,那这个解就太不靠谱了。所以这个方程组系统就是ill-conditioned病态的,不正常的,不稳定的,有问题的。右边那个就叫well-condition。