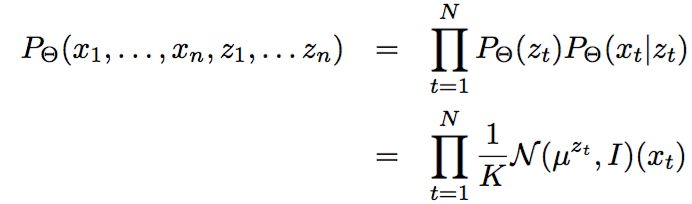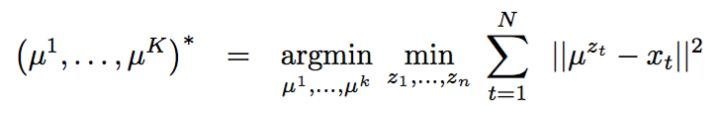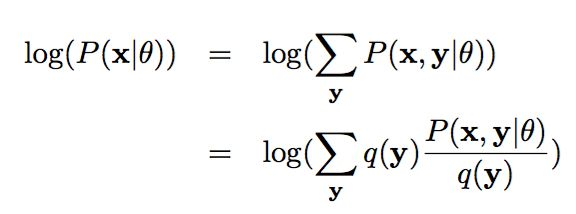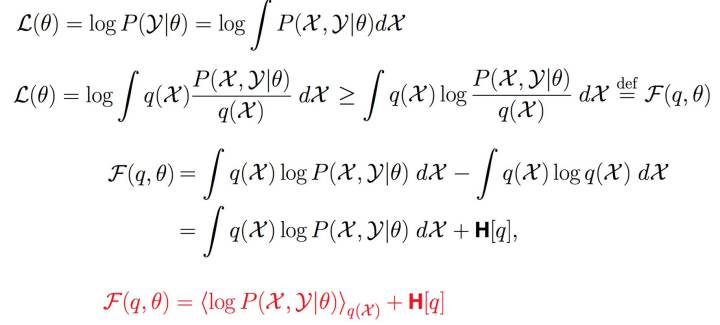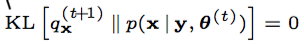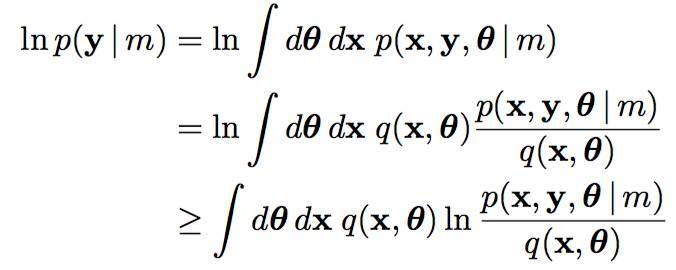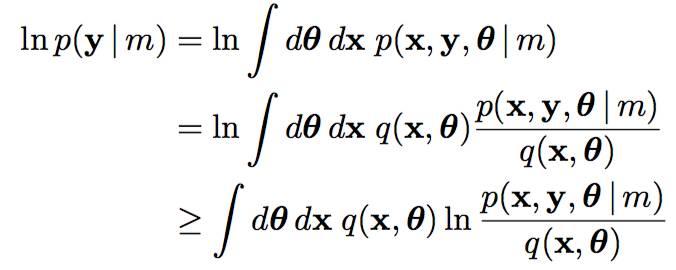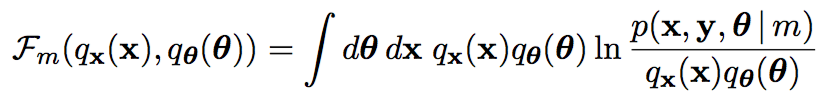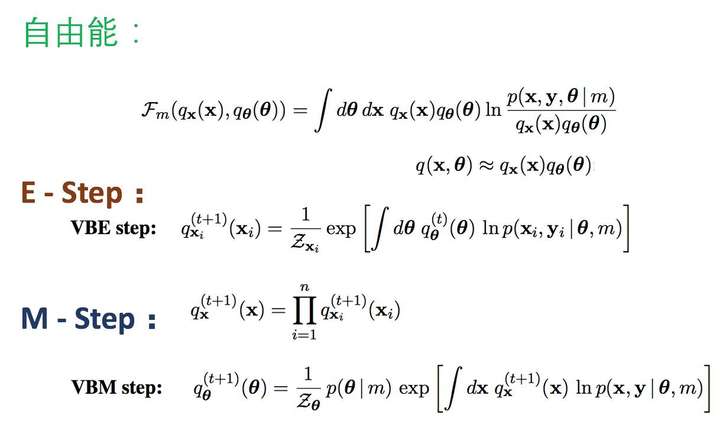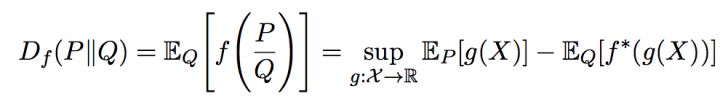EM算法理解的九层境界
EM 就是 E + M EM 是一种局部下限构造 K-Means是一种Hard EM算法 从EM 到 广义EM 广义EM的一个特例是VBEM 广义EM的另一个特例是WS算法 广义EM的再一个特例是Gibbs抽样算法 WS算法是VAE和GAN组合的简化版 KL距离的统一
第一层境界, EM算法就是E 期望 + M 最大化
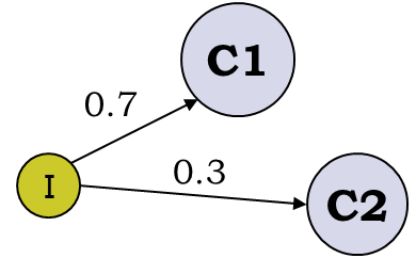
最经典的例子就是抛3个硬币,跑I硬币决定C1和C2,然后抛C1或者C2决定正反面, 然后估算3个硬币的正反面概率值。
<img src="https://pic1.zhimg.com/50/v2-4b710bbd48f9320f928a6b54a3e5d551_hd.jpg" data-caption="" data-size="normal" data-rawwidth="418" data-rawheight="262" class="content_image" width="418"/> 这个例子为什么经典, 因为它告诉我们,当存在隐变量I的时候 , 直接的最大似然估计无法直接搞定。 什么是隐变量?为什么要引入隐变量? 对隐变量的理解是理解EM算法的第一要义 !Chuong B Do & Serafim Batzoglou的Tutorial论文“What is the expectation maximization algorithm?”对此有详细的例子进行分析。
通过隐变量,我们第一次解读了EM算法的伟大!突破了直接MLE的限制(不详细解释了)。
至此, 你理解了EM算法的第一层境界,看山是山 。
第二层境界, EM算法就一种局部下限构造
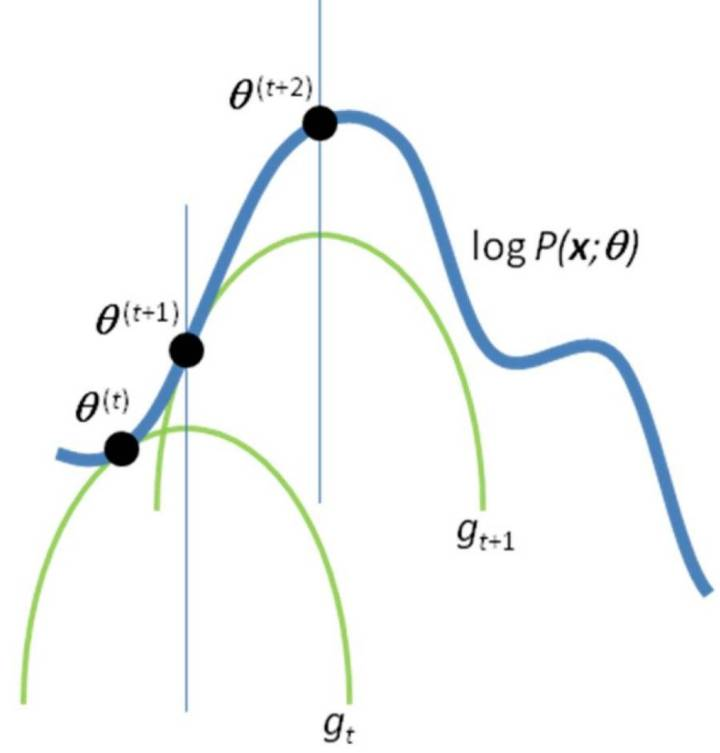
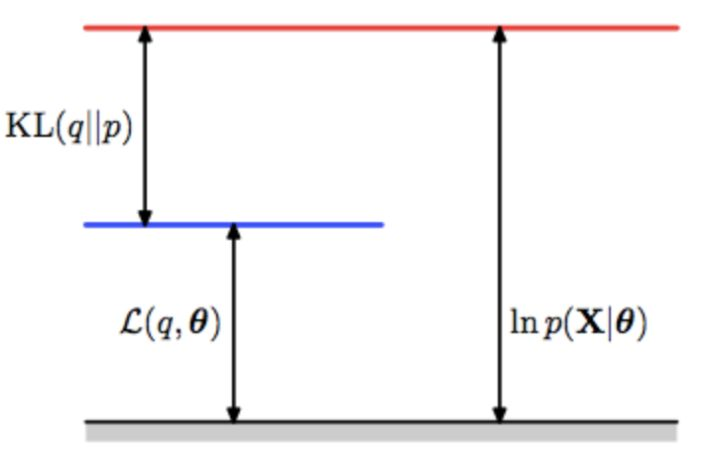
如果你再深入到基于隐变量的EM算法的收敛性证明, 基于log(x)函数的Jensen不等式构造, 我们很容易证明,EM算法是在反复的构造新的下限,然后进一步求解 。
<img src="https://pic1.zhimg.com/50/v2-a38b6748f36f0cb9bcd43b5ca435e5c6_hd.jpg" data-caption="" data-size="small" data-rawwidth="788" data-rawheight="880" class="origin_image zh-lightbox-thumb" width="788" data-original="https://pic1.zhimg.com/v2-a38b6748f36f0cb9bcd43b5ca435e5c6_r.jpg"/> 所以,先固定当前参数, 计算得到当前隐变量分布的一个下届函数, 然后优化这个函数, 得到新的参数, 然后循环继续。
<img src="https://pic3.zhimg.com/50/v2-21baf3526bae725faad475b5cd75e324_hd.jpg" data-caption="" data-size="small" data-rawwidth="1044" data-rawheight="1092" class="origin_image zh-lightbox-thumb" width="1044" data-original="https://pic3.zhimg.com/v2-21baf3526bae725faad475b5cd75e324_r.jpg"/> 也正是这个不停的构造下限的思想未来和VB方法联系起来了。 如果你理解了这个, 恭喜你, 进入理解EM算法的第二层境界, 看山看石 。
第三层境界, K-均值方法是一种Hard EM算法
在第二层境界的基础上, 你就能随意傲游EM算法用到GMM和HMM模型中去了。 尤其是对GMM的深入理解之后, 对于有隐变量的联合概率,如果利用高斯分布代入之后:
很容易就和均方距离建立联系:
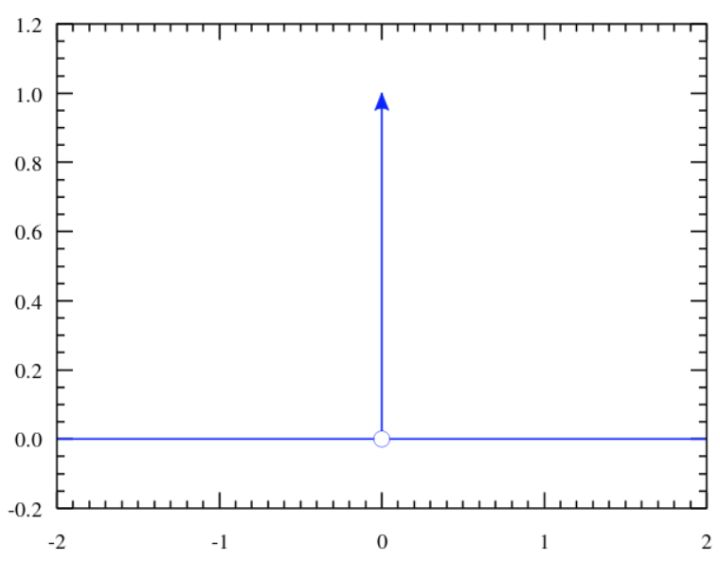
<img src="https://pic3.zhimg.com/50/v2-0e237f8a914a732b87599a0dea0c8367_hd.jpg" data-caption="" data-size="small" data-rawwidth="728" data-rawheight="118" class="origin_image zh-lightbox-thumb" width="728" data-original="https://pic3.zhimg.com/v2-0e237f8a914a732b87599a0dea0c8367_r.jpg"/> 但是,能不能说K-均值就是高斯分布的EM算法呢?不是, 这里虽然拓展到了相同的距离公式, 但是背后逻辑还是不一样, 不一样在哪里呢?K-均值在讨论隐变量的决定时候,用的是dirac delta 分布, 这个分布是高斯分布的一种极限 。
<img src="https://pic2.zhimg.com/50/v2-6f5e3027ff448d470d2cb5695dceb3cf_hd.jpg" data-caption="" data-size="small" data-rawwidth="760" data-rawheight="592" class="origin_image zh-lightbox-thumb" width="760" data-original="https://pic2.zhimg.com/v2-6f5e3027ff448d470d2cb5695dceb3cf_r.jpg"/> <img src="https://pic3.zhimg.com/50/v2-a970065b4e35ac6f94f86b8f94f1df05_hd.gif" data-caption="" data-size="normal" data-rawwidth="200" data-rawheight="335" data-thumbnail="https://pic3.zhimg.com/50/v2-a970065b4e35ac6f94f86b8f94f1df05_hd.jpg" class="content_image" width="200"/>
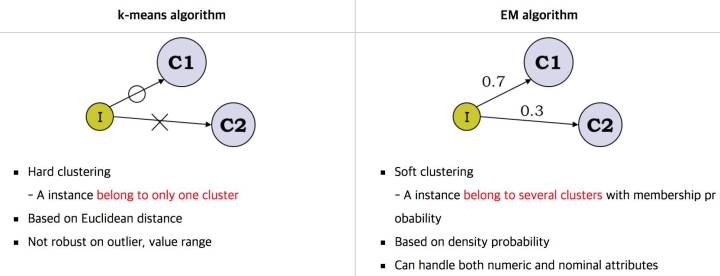
如果你觉得这个扩展不太好理解, 那么更为简单直观的就是, k-均值用的hard EM算法, 而我们说的EM算法是soft EM算法。 所谓hard 就是要么是,要么不是0-1抉择。 而Soft是0.7比例是c1,0.3比例是c2的情况。
<img src="https://pic2.zhimg.com/50/v2-1c1d5d2b658b4e9580a051f955df7b48_hd.jpg" data-caption="" data-size="normal" data-rawwidth="1664" data-rawheight="638" class="origin_image zh-lightbox-thumb" width="1664" data-original="https://pic2.zhimg.com/v2-1c1d5d2b658b4e9580a051f955df7b48_r.jpg"/> 那么充分理解了k-均值和EM算法本身的演化和差异有什么帮助呢?让你进一步理解到隐变量是存在一种分布的 。
<img src="https://pic3.zhimg.com/50/v2-1cb36ffe3e6b918080b16627389395a5_hd.jpg" data-caption="" data-size="normal" data-rawwidth="576" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="576" data-original="https://pic3.zhimg.com/v2-1cb36ffe3e6b918080b16627389395a5_r.jpg"/> 如果你理解了这个, 恭喜你, 进入理解EM算法的第三层境界, 看山看峰 。
第四层境界,EM 是 广义EM的特例
通过前3层境界, 你对EM算法的理解要跨过隐变量, 进入隐分布的境界 。 如果我们把前面的EM收敛证明稍微重复一下,但是引入隐分布 。
<img src="https://pic4.zhimg.com/50/v2-866e11172dc0fba6daefa9f370411b11_hd.jpg" data-caption="" data-size="small" data-rawwidth="1830" data-rawheight="826" class="origin_image zh-lightbox-thumb" width="1830" data-original="https://pic4.zhimg.com/v2-866e11172dc0fba6daefa9f370411b11_r.jpg"/> 这样我们把Jensen不等收右边的部分定义为自由能(如果你对自由能有兴趣,请参考“
给能量以自由吧! ”,如果没有兴趣, 你就视为一种命名)。 那么
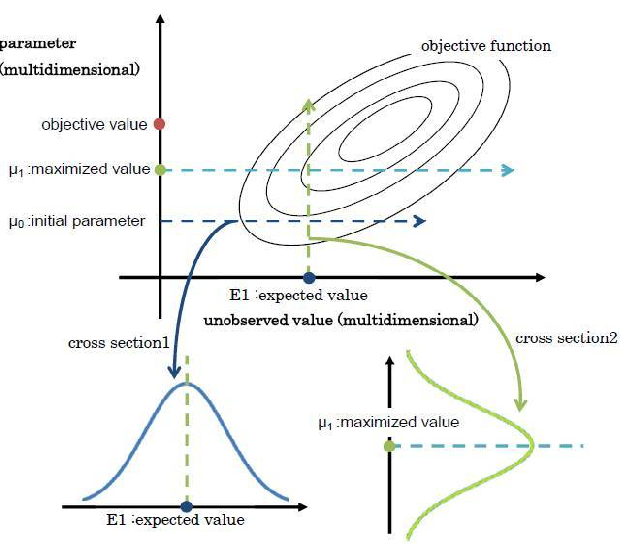
E步骤是固定参数优化隐分布, M步骤是固定隐分布优化参数,这就是广义EM算法了 。
有了广义EM算法之后, 我们对自由能深入挖掘, 发现自由能和似然度和KL距离之间的关系:
<img src="https://pic3.zhimg.com/50/v2-47d2d736c98ab6bf95e56f66620f3fc7_hd.jpg" data-caption="" data-size="small" data-rawwidth="1534" data-rawheight="562" class="origin_image zh-lightbox-thumb" width="1534" data-original="https://pic3.zhimg.com/v2-47d2d736c98ab6bf95e56f66620f3fc7_r.jpg"/> 所以固定参数的情况下, 那么只能最优化KL距离了, 那么隐分布只能取如下分布:
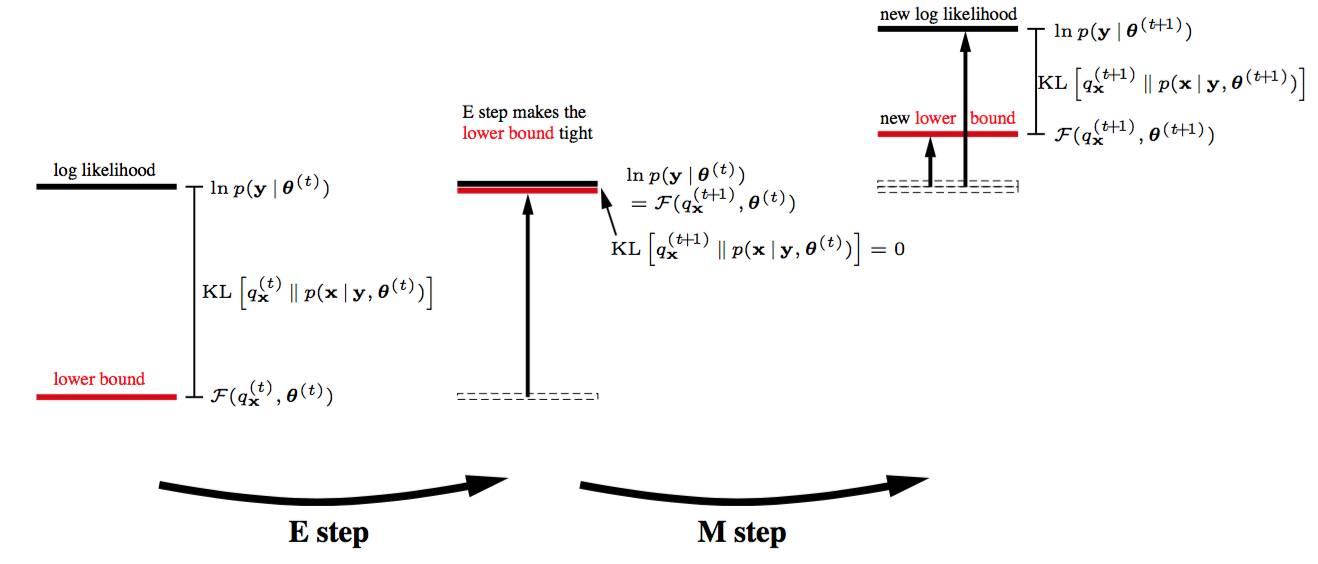
<img src="https://pic1.zhimg.com/50/v2-28aa54c91428fa32a93fe7243034e70f_hd.jpg" data-caption="" data-size="small" data-rawwidth="650" data-rawheight="138" class="origin_image zh-lightbox-thumb" width="650" data-original="https://pic1.zhimg.com/v2-28aa54c91428fa32a93fe7243034e70f_r.jpg"/> 而这个在EM算法里面是直接给出的 。 所以EM算法是广义EM算法的天然最优的隐分布情况。 但是很多时候隐分布不是那么容易计算的!
前面的推理虽然很简单, 但是要理解到位真心不容易, 首先要深入理解KL距离是如何被引入的?
<img src="https://pic3.zhimg.com/50/v2-5fb1549c245298846063a9742cb11e1a_hd.jpg" data-caption="" data-size="small" data-rawwidth="726" data-rawheight="468" class="origin_image zh-lightbox-thumb" width="726" data-original="https://pic3.zhimg.com/v2-5fb1549c245298846063a9742cb11e1a_r.jpg"/> 其次要理解, 为什么传统的EM算法, 不存在第一个最优化 ?因为在没有限制的隐分布(天然情况下) 情况下, 第一个最优就是要求:
<img src="https://pic3.zhimg.com/50/v2-227eccdac2131d6e0538d83515444624_hd.jpg" data-caption="" data-size="normal" data-rawwidth="304" data-rawheight="44" class="content_image" width="304"/> 而这个隐分布, EM算法里面是直接给出的,而不是让你证明得到的。
<img src="https://pic2.zhimg.com/50/v2-2004ef50d0796d32e6cd61ac7a6cdf2d_hd.jpg" data-caption="" data-size="small" data-rawwidth="1318" data-rawheight="564" class="origin_image zh-lightbox-thumb" width="1318" data-original="https://pic2.zhimg.com/v2-2004ef50d0796d32e6cd61ac7a6cdf2d_r.jpg"/> 这样, 在广义EM算法中,你看到两个优化步骤,我们进入了两个优化步骤理解EM算法的境界了。 如果你理解了这个, 恭喜你, 进入理解EM算法的第四层境界, 有水有山 。
第五层境界,广义EM的一个特例是VBEM
在隐分布没有限制的时候, 广义EM算法就是EM算法, 但是如果隐分布本身是有限制的呢?譬如有个先验分布的限制, 譬如有计算的限制呢 ?
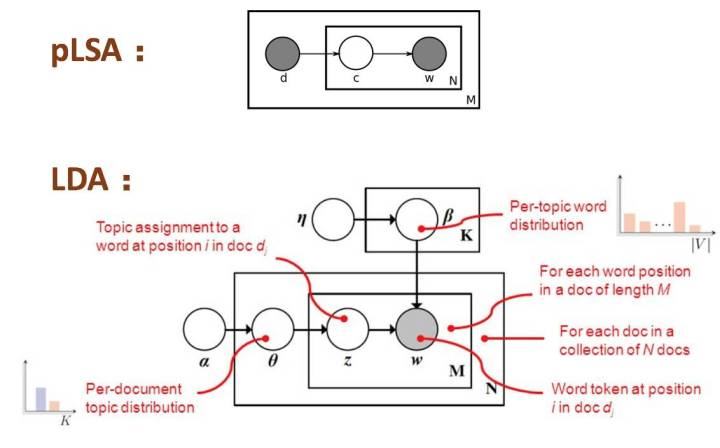
例如先验分布的限制:从pLSA到LDA就是增加了参数的先验分布!
<img src="https://pic3.zhimg.com/50/v2-a868b18611aa43395d534f94ebcd8221_hd.jpg" data-caption="" data-size="small" data-rawwidth="1132" data-rawheight="704" class="origin_image zh-lightbox-thumb" width="1132" data-original="https://pic3.zhimg.com/v2-a868b18611aa43395d534f94ebcd8221_r.jpg"/> 例如计算上的限制:mean-field计算简化的要求,分量独立。
<img src="https://pic4.zhimg.com/50/v2-76ce9f52d2056f07ebeecae6daefffc6_hd.jpg" data-caption="" data-size="normal" data-rawwidth="594" data-rawheight="388" class="origin_image zh-lightbox-thumb" width="594" data-original="https://pic4.zhimg.com/v2-76ce9f52d2056f07ebeecae6daefffc6_r.jpg"/> 诸如此类限制, 都使得广义EM里面的第一步E优化不可能达到无限制最优, 所以KL距离无法为0 。
<img src="https://pic4.zhimg.com/50/v2-2c76444860b4fbfad17b8978c18f1cda_hd.jpg" data-caption="" data-size="small" data-rawwidth="1340" data-rawheight="606" class="origin_image zh-lightbox-thumb" width="1340" data-original="https://pic4.zhimg.com/v2-2c76444860b4fbfad17b8978c18f1cda_r.jpg"/>
基于有限制的理解 , 再引入模型变分的思想 , 根据模型m的变化, 对应参数和隐变量都有相应的分布:
<img src="https://pic4.zhimg.com/50/v2-61d3e0b57ce1346d67b790911dcd4e36_hd.jpg" data-caption="" data-size="small" data-rawwidth="676" data-rawheight="270" class="origin_image zh-lightbox-thumb" width="676" data-original="https://pic4.zhimg.com/v2-61d3e0b57ce1346d67b790911dcd4e36_r.jpg"/> 并且满足分布独立性简化计算的假设:
<img src="https://pic3.zhimg.com/50/v2-1ce20565b6baec192a5fabdb3e3c2370_hd.jpg" data-caption="" data-size="normal" data-rawwidth="306" data-rawheight="52" class="content_image" width="306"/> 在变分思想下, 自由能被改写了:
<img src="https://pic4.zhimg.com/50/v2-f9f283ed1adc265c6b54b5b7fd1dcbc1_hd.jpg" data-caption="" data-size="small" data-rawwidth="824" data-rawheight="96" class="origin_image zh-lightbox-thumb" width="824" data-original="https://pic4.zhimg.com/v2-f9f283ed1adc265c6b54b5b7fd1dcbc1_r.jpg"/> 这样我们就得到了VBEM算法了:
<img src="https://pic3.zhimg.com/50/v2-d3ae8be76ce5f2e4f5bc7b85a926b0de_hd.jpg" data-caption="" data-size="small" data-rawwidth="1218" data-rawheight="712" class="origin_image zh-lightbox-thumb" width="1218" data-original="https://pic3.zhimg.com/v2-d3ae8be76ce5f2e4f5bc7b85a926b0de_r.jpg"/>
第六层境界,广义EM的另一个特例是WS算法
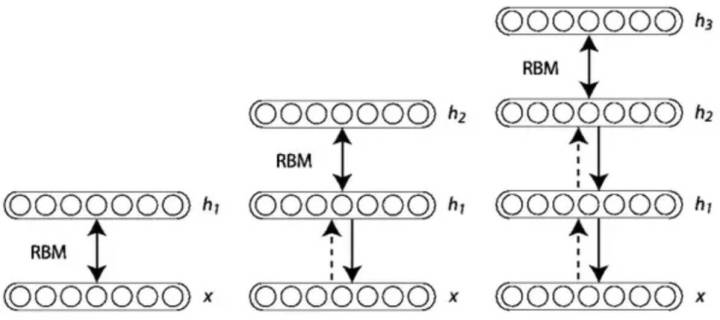
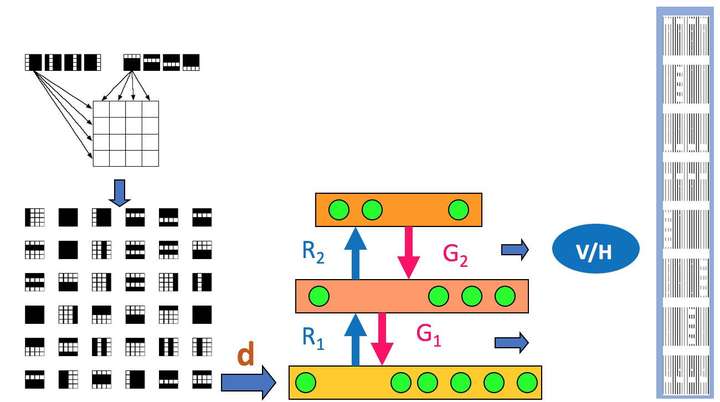
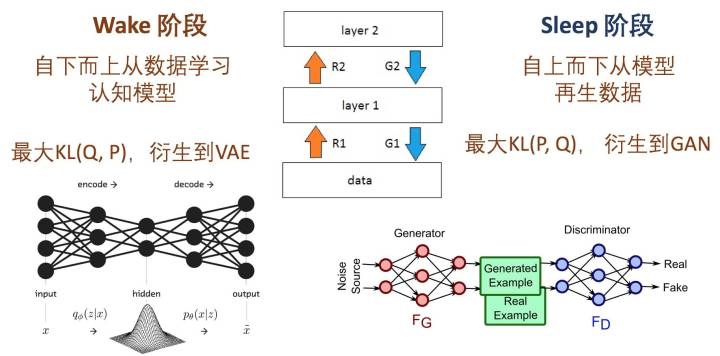
Hinton老爷子搞定VBEM算法后, 并没有停滞, 他在研究DBN和DBM的Fine-Tuning的时候, 提出了Wake-Sleep算法。 我们知道在有监督的Fine-Tuning可以使用BP算法, 但是无监督的Fine-Tuning,使用的是Wake-Sleep算法。
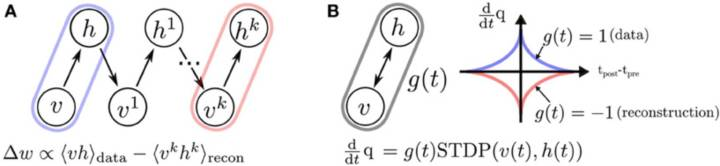
<img src="https://pic1.zhimg.com/50/v2-286f9939e821cd3f0632806738ab01a0_hd.jpg" data-caption="" data-size="small" data-rawwidth="1196" data-rawheight="532" class="origin_image zh-lightbox-thumb" width="1196" data-original="https://pic1.zhimg.com/v2-286f9939e821cd3f0632806738ab01a0_r.jpg"/> 就是这个WS算法,也是广义EM算法的一种特例。 WS算法分为认知阶段和生成阶段。
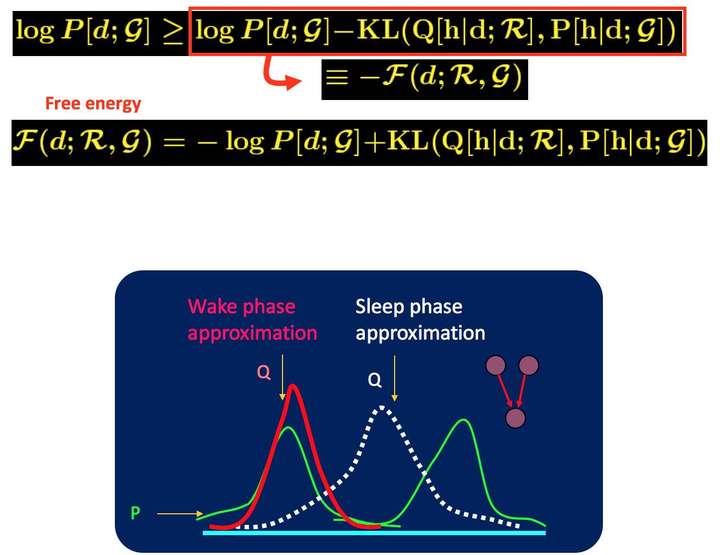
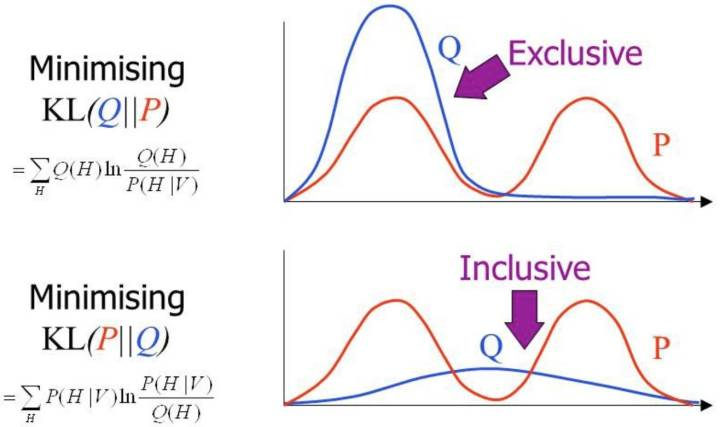
<img src="https://pic4.zhimg.com/50/v2-3cedb136d8aa7808071ffccb0ae18217_hd.jpg" data-caption="" data-size="small" data-rawwidth="1300" data-rawheight="726" class="origin_image zh-lightbox-thumb" width="1300" data-original="https://pic4.zhimg.com/v2-3cedb136d8aa7808071ffccb0ae18217_r.jpg"/> 在前面自由能里面,我们将KL距离引入了, 这里刚好这两个阶段分别优化了KL距离的两种形态。 固定P优化Q,和固定Q优化P 。
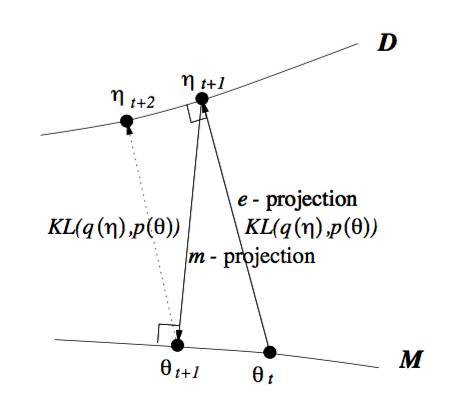
<img src="https://pic4.zhimg.com/50/v2-ae5fcf55ed247450ce8084ea43b8bc3b_hd.jpg" data-caption="" data-size="small" data-rawwidth="1310" data-rawheight="1010" class="origin_image zh-lightbox-thumb" width="1310" data-original="https://pic4.zhimg.com/v2-ae5fcf55ed247450ce8084ea43b8bc3b_r.jpg"/> 所以当我们取代自由能理解, 全部切换到KL距离的理解, 广义EM算法的E步骤和M步骤就分别是E投影和M投影。 因为要求KL距离最优, 可以等价于垂直。 而这个投影, 可以衍生到数据D的流形空间, 和模型M的流形空间 。
<img src="https://pic1.zhimg.com/50/v2-468b515b4d26ebc4765f82bf3ed1c3bf_hd.jpg" data-caption="" data-size="normal" data-rawwidth="464" data-rawheight="406" class="origin_image zh-lightbox-thumb" width="464" data-original="https://pic1.zhimg.com/v2-468b515b4d26ebc4765f82bf3ed1c3bf_r.jpg"/> 所以你认同WS算法是一种广义EM算法(GEM)之后, 基于KL距离再认识GEM算法。 引入了数据流形和模型流形。 引入了E投影和M投影。
不过要注意的wake识别阶段对应的是M步骤, 而sleep生成阶段对应的E步骤。 所以WS算法对应的是广义ME算法 。 如果你理解了这个, 恭喜你, 进入理解EM算法的第六层境界, 山高水深 。
第七层境界,广义EM的再一个特例是Gibbs Sampling
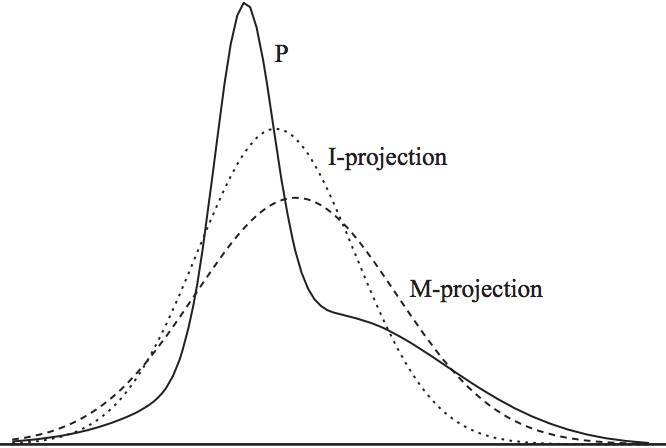
其实,前面基于KL距离的认知, 严格放到信息理论的领域, 对于前面E投影和M投影都有严格的定义。 M投影的名称是类似的,但是具体是moment projection,但是E投影应该叫I投影,具体是information projection 。
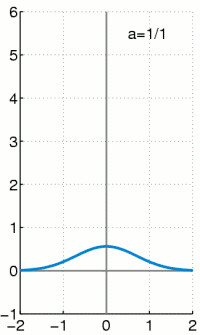
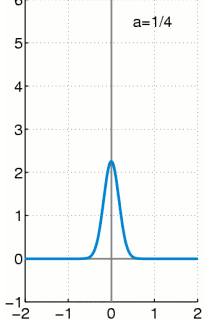
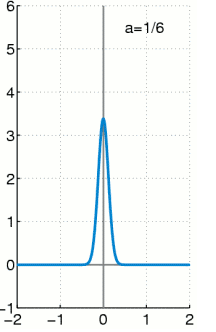
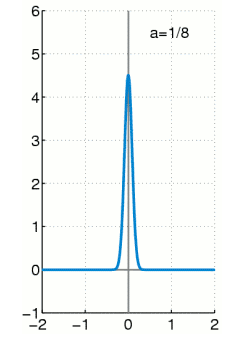
<img src="https://pic3.zhimg.com/50/v2-bb16f97e3b82fb113b8ba475b6e51164_hd.jpg" data-caption="" data-size="small" data-rawwidth="666" data-rawheight="448" class="origin_image zh-lightbox-thumb" width="666" data-original="https://pic3.zhimg.com/v2-bb16f97e3b82fb113b8ba475b6e51164_r.jpg"/> 上面这种可能不太容易体会到M投影和I投影的差异, 如果再回到最小KL距离,有一个经典的比较。 可以体会M投影和I投影的差异。 上面是I投影,只覆盖一个峰。 下面是M投影, 覆盖了两个峰。
<img src="https://pic4.zhimg.com/50/v2-891a8c795f084923d7d913936af335ed_hd.jpg" data-caption="" data-size="small" data-rawwidth="1316" data-rawheight="780" class="origin_image zh-lightbox-thumb" width="1316" data-original="https://pic4.zhimg.com/v2-891a8c795f084923d7d913936af335ed_r.jpg"/> 当我们不是直接计算KL距离, 而是基于蒙特卡洛抽样方法来估算KL距离 。
<img src="https://pic1.zhimg.com/50/v2-6e39522a095e0d417634fd9d84253531_hd.jpg" data-caption="" data-size="small" data-rawwidth="1012" data-rawheight="716" class="origin_image zh-lightbox-thumb" width="1012" data-original="https://pic1.zhimg.com/v2-6e39522a095e0d417634fd9d84253531_r.jpg"/> 有兴趣对此深入的,可以阅读论文“On Monte Carlo methods for estimating ratios of normalizing constants”
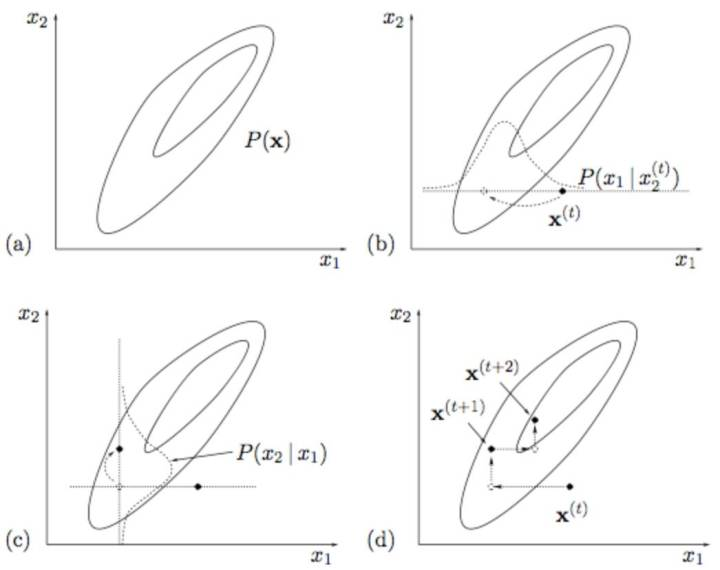
这时候, 广义EM算法,就是Gibbs Sampling了。 所以Gibbs Sampling,本质上就是采用了蒙特卡洛方法计算的广义EM算法。
<img src="https://pic3.zhimg.com/50/v2-934635b34223baace727b634aa50c13f_hd.jpg" data-caption="" data-size="small" data-rawwidth="695" data-rawheight="664" class="origin_image zh-lightbox-thumb" width="695" data-original="https://pic3.zhimg.com/v2-934635b34223baace727b634aa50c13f_r.jpg"/> 所以, 如果把M投影和I投影看成是一个变量上的最小距离点,那么Gibbs Sampling和广义EM算法的收敛过程是一致的 。
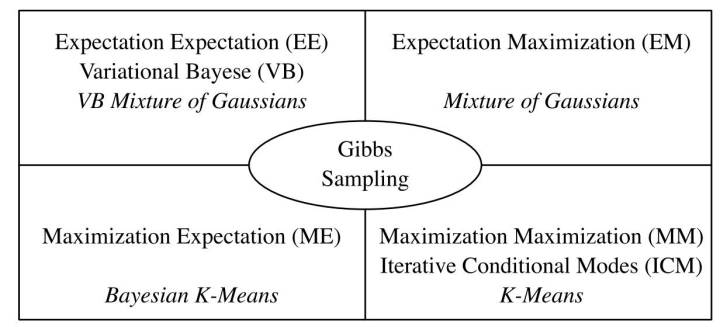
<img src="https://pic2.zhimg.com/50/v2-58cb1338ae2e5dee38cce4b2ef44e4e8_hd.jpg" data-caption="" data-size="small" data-rawwidth="1046" data-rawheight="828" class="origin_image zh-lightbox-thumb" width="1046" data-original="https://pic2.zhimg.com/v2-58cb1338ae2e5dee38cce4b2ef44e4e8_r.jpg"/> VAE的发明者,Hinton的博士后, Max Welling在论文“Bayesian K-Means as a “Maximization-Expectation” Algorithm”中, 对这种关系有如下很好的总结!
<img src="https://pic2.zhimg.com/50/v2-c09456c8096cf7625b6292e2142dbfd3_hd.jpg" data-caption="" data-size="small" data-rawwidth="1232" data-rawheight="560" class="origin_image zh-lightbox-thumb" width="1232" data-original="https://pic2.zhimg.com/v2-c09456c8096cf7625b6292e2142dbfd3_r.jpg"/> 另外, Zoubin Ghahramani, Jordan的博士, 在“Factorial Learning and the EM Algorithm”等相关论文也反复提到他们之间的关系。
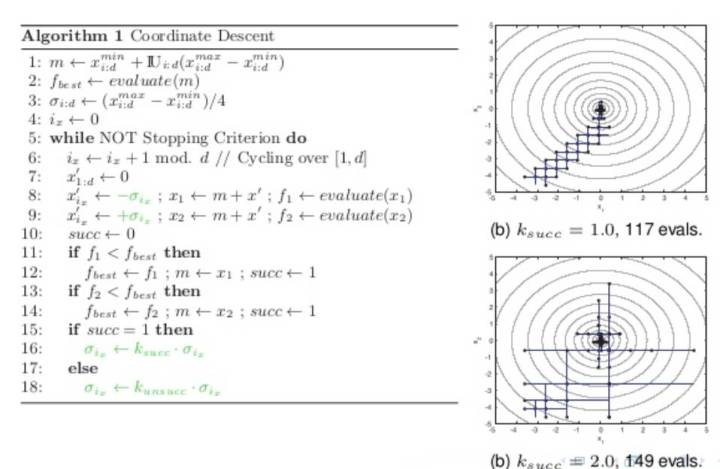
这样, 通过广义EM算法把Gibbs Sampling和EM, VB, K-Means和WS算法全部联系起来了。 有了Gibbs Sampling的背书, 你是不是能更好的理解, 为什么WS算法可以是ME步骤,而不是EM的步骤呢?另外,我们知道坐标下降Coordinate Descent也可以看成一种Gibbs Sampling过程, 如果有人把Coordinate Descent和EM算法联系起来, 你还会觉得奇怪么?
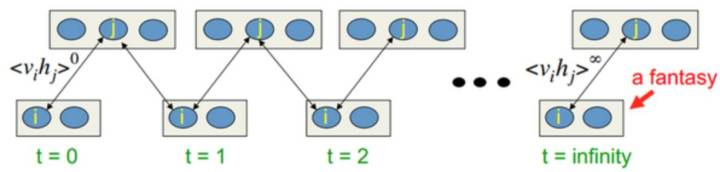
<img src="https://pic4.zhimg.com/50/v2-c2e9aabea1d26cb927d553dd8e16b339_hd.jpg" data-caption="" data-size="small" data-rawwidth="958" data-rawheight="624" class="origin_image zh-lightbox-thumb" width="958" data-original="https://pic4.zhimg.com/v2-c2e9aabea1d26cb927d553dd8e16b339_r.jpg"/> 现在我们发现VB和Gibbs Sampling都可以放到广义EM的大框架 下, 只是求解过程一个采用近似逼近, 一个采用蒙特卡洛采样。 有了EM算法和Gibbs Sampling的关系, 现在你理解, 为什么Hinton能够发明CD算法 了么? 细节就不展开了。
<img src="https://pic4.zhimg.com/50/v2-de39e478652bd2fd7231e33722bd153f_hd.jpg" data-caption="" data-size="small" data-rawwidth="1192" data-rawheight="284" class="origin_image zh-lightbox-thumb" width="1192" data-original="https://pic4.zhimg.com/v2-de39e478652bd2fd7231e33722bd153f_r.jpg"/>
第八层境界,WS算法是VAE和GAN组合的简化版
Jordan的弟子邢波老师,他的学生胡志挺,发表了一篇文章, On Unifying Deep Generative Models,试图通过WS算法,统一对VAE和GAN的理解。
<img src="https://pic3.zhimg.com/50/v2-bce08a8d1984cb36e2f699eb5b4425d2_hd.jpg" data-caption="" data-size="small" data-rawwidth="1826" data-rawheight="902" class="origin_image zh-lightbox-thumb" width="1826" data-original="https://pic3.zhimg.com/v2-bce08a8d1984cb36e2f699eb5b4425d2_r.jpg"/>
对
VAE的理解, 变了加了正则化的KL距离, 而对于GAN的理解变成了加Jensen–Shannon 散度 。 所以, 当我们把广义EM算法的自由能, 在WS算法中看成KL散度, 现在看成扩展的KL散度。 对于正则化扩展, 有很多类似论文, “Mode Regularized Generative Adversarial Networks”, “Stabilizing Training of Generative Adversarial Networks through Regularization” 有兴趣可以读读。
所以对于VAE,类比WS算法的Wake认知阶段, 不同的是在ELBO这个VBEM目标的基础上加了KL散度作为正则化限制。 再应用再参数化技巧实现了VAE 。
<img src="https://pic3.zhimg.com/50/v2-856f23800b7806346d32617ffac58dad_hd.jpg" data-caption="" data-size="small" data-rawwidth="1226" data-rawheight="742" class="origin_image zh-lightbox-thumb" width="1226" data-original="https://pic3.zhimg.com/v2-856f23800b7806346d32617ffac58dad_r.jpg"/> 而对应到GAN,类比Sleep阶段,正则化限制换了JSD距离, 然后目标KL距离也随着不同GAN的变体也可以变化 。
所以, VAE和GAN都可以理解为有特殊正则化限制的Wake-Sleep步骤, 那么组合起来也并不奇怪。
<img src="https://pic1.zhimg.com/50/v2-06d46afb8aeed812b4e90f7befbe56cd_hd.jpg" data-caption="" data-size="small" data-rawwidth="2066" data-rawheight="246" class="origin_image zh-lightbox-thumb" width="2066" data-original="https://pic1.zhimg.com/v2-06d46afb8aeed812b4e90f7befbe56cd_r.jpg"/> 这就是为什么那么多论文研究如何组合VAE/GAN到同一个框架下面去。目前对这方面的理解还在广泛探讨中。
如果你理解了这个, 恭喜你, 进入理解EM算法的第八层境界, 水中有水、山外有山 。
第九层境界,KL距离的统一
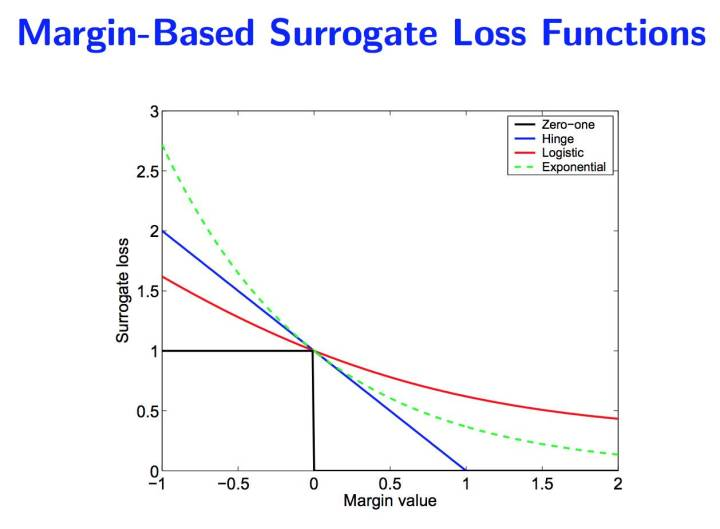
Jordan 大佬的一片论文, 开启了KL距离的统一, “On surrogate loss functions and f-divergences”。 里面对于所谓的正反KL距离全部统一到 f 散度的框架下面。 Jordan 首先论述了对于损失函数统一的Margin理论的意义 。
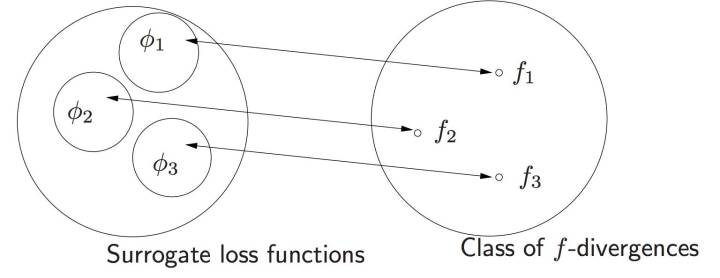
<img src="https://pic2.zhimg.com/50/v2-c5cb9b042bca75db22ee685b9a0ad05d_hd.jpg" data-caption="" data-size="small" data-rawwidth="1258" data-rawheight="924" class="origin_image zh-lightbox-thumb" width="1258" data-original="https://pic2.zhimg.com/v2-c5cb9b042bca75db22ee685b9a0ad05d_r.jpg"/> 然后把这些损失函数也映射到 f 散度 :
然后微软的 Sebastian Nowozin, 把 f-散度扩展到GAN “f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization”。
然后对
正反KL散度也做了一次统一 。
对于 f-散度的理解离不开对Fenchel对偶的理解。
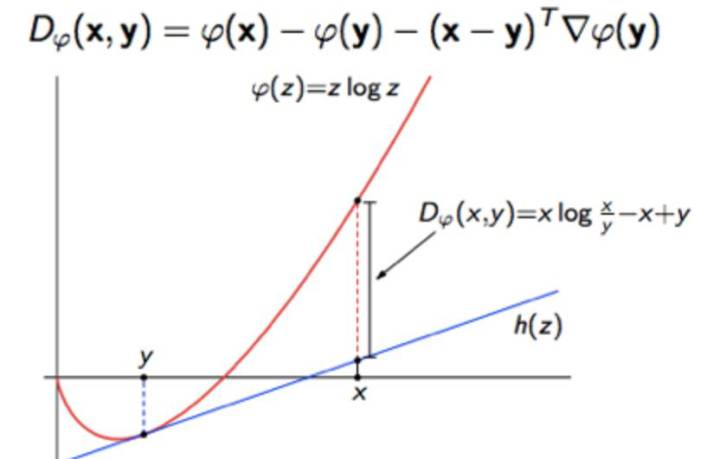
<img src="https://pic4.zhimg.com/50/v2-8baaac19cab3f150c684870f57ddbbab_hd.jpg" data-caption="" data-size="small" data-rawwidth="990" data-rawheight="140" class="origin_image zh-lightbox-thumb" width="990" data-original="https://pic4.zhimg.com/v2-8baaac19cab3f150c684870f57ddbbab_r.jpg"/> 除了f-散度, 还有人基于bregman散度去统一正反KL散度的认知。 KL散度就是香农熵的bregman散度。
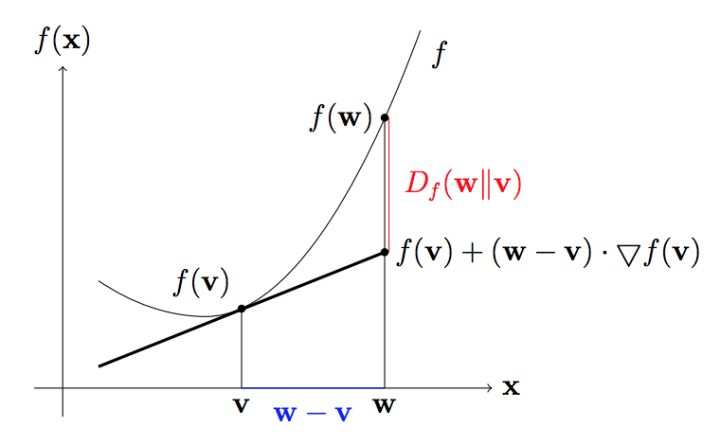
<img src="https://pic4.zhimg.com/50/v2-1a59a80f718dc7d4c35ea19c456ead64_hd.jpg" data-caption="" data-size="small" data-rawwidth="832" data-rawheight="530" class="origin_image zh-lightbox-thumb" width="832" data-original="https://pic4.zhimg.com/v2-1a59a80f718dc7d4c35ea19c456ead64_r.jpg"/> 而Bregman散度本身是基于一阶泰勒展开的一种偏离度的度量。
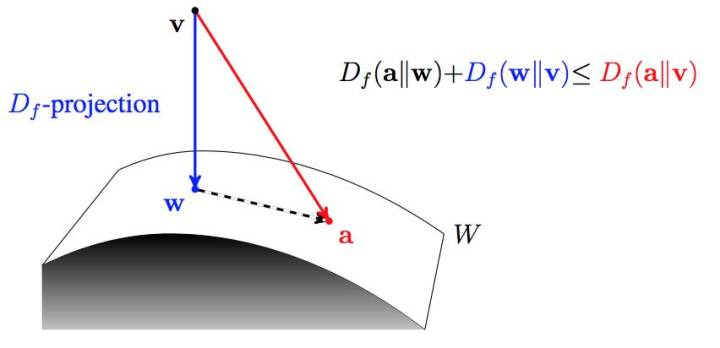
然后再基于Bregman距离去研究最小KL投影, 函数空间采用香农熵(参考“信息熵的由来 ”)。
<img src="https://pic3.zhimg.com/50/v2-0b3d448679d2e1d644fc8f4e6f121349_hd.jpg" data-caption="" data-size="small" data-rawwidth="852" data-rawheight="412" class="origin_image zh-lightbox-thumb" width="852" data-original="https://pic3.zhimg.com/v2-0b3d448679d2e1d644fc8f4e6f121349_r.jpg"/> 无论f-散度还是bregman散度对正反KL距离的统一, 之后的广义EM算法, 都会变得空间的最优投影的交替出现 。 或许广义EM算法也成了不同流形空间上的坐标梯度下降算法而已coodinate descent。
如果你理解了这个, 恭喜你, 进入理解EM算法的第九层境界,山水合一 。
小结
这里浅薄的介绍了理解EM算法的9层境界,托名Hinton和Jordan,着实是因为佩服他们俩和各自的弟子们对EM算法,甚至到无监督深度学习的理解和巨大贡献。想来Hinton和Jordan对此必定会有更为深刻的理解, 很好奇会到何种程度 。。。 最后依然好奇, 为啥只有他们两家的子弟能够不停的突破无监督深度学习?Hinton 老仙说, 机器学习的未来在于无监督学习!