信息，熵，联合熵，条件熵，互信息（信息增益），交叉熵，相对熵（KL散度） - 走看看

zoukankan html css js c++ java

信息，熵，联合熵，条件熵，互信息（信息增益），交叉熵，相对熵（KL散度）

自信息

自信息I表示概率空间中的单一事件或离散随机变量的值相关的信息量的量度。它用信息的单位表示，例如bit、nat或是hart，使用哪个单位取决于在计算中使用的对数的底。如下图：

对数以2为底，单位是比特（bit）

对数以e为底，单位是纳特（nat）

如英语有26个字母，假设在文章中出现的概率相等，每个字母的自信息量（也称作编码长度，也就是在最优情况下，应该用多少比特去表示字母）为：

对该自信息的期望就是熵。可以看出当字母出现概率越大时，表示该字母所应该用的比特数也越少，这也就是传说中的哈夫曼编码(Huffman Coding)。

若现在假设文章中仅仅等概率存在A，B，C，则这三个字母的自信息为：

则我们只需要用两个比特（也就是00,01,10）就可以表示一篇文章。

因此变量越均匀分布，自信息的期望就越大，也就熵越大（平均编码长度越长），也即最优表示变量所需用到比特数量的期望则越多，也能说明文章挈带的信息量就越多，把文章搞清楚所需要的信息量也就越大（比特数多了）。

熵

熵在物理上是表示混乱程度，在信息论中，信息熵用以下方程表示,也就是对分布自信息的期望，单位取决于在计算中使用的对数的底：

E为期望函数，p为概率质量函数，I为自信息函数

离散的表达式：

若为概率为连续型，则要用积分去求

若概率越为均匀分布，则熵越大，变量的不确定性越大，把它搞清楚所需要的信息量也就越大。如AvsB，A队的胜率为100%，则我们不需要任何信息都能搞清楚A队肯定赢。但是若A队和B队的胜率各为50%，则我们要将哪队获胜确定下来所需要的信息量很大。

设随机变量 $X$ 为抛一枚均匀硬币的取值，其中正面朝上用 $1$ 表示，反面朝上用 $0$ 表示，于是有：
$Pleft{ X=0，1 ight}= frac{1}{2}$ 注：由于 $X=0,X=1$ 概率均相等，为了版面整洁故合并表示。这里的log是以2为底的：

$H(X)=- frac{1}{2} imes log frac{1}{2} - frac{1}{2} imes log frac{1}{2}=1$

联合信息熵

联合信息熵的定义如下：

条件信息熵

条件信息熵的定义如下：

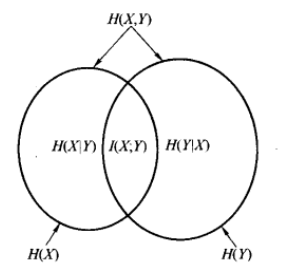
用图像形象化地理解这联合信息熵与条件信息熵的关系：

熵的关系图

举个栗子，今天的天气是什么可以看作为事件X，我是否穿短袖可看作事件Y。这两个事件可以构成联合概率分布p(X,Y)，其联合熵为上述关系图的第一条

注意，两个事件加起来的信息量(H(X,Y))肯定是大于等于单个事件的信息量(H(X)或H(Y))的。同时，天气如何与我是否穿短袖这两个事件并不是独立的，
因此已知今天天气的情况下，我是否穿衣的信息量/不确定度是减少了的。所以已知H(X)这个信息量时，联合分布H(X,Y)剩余的信息量就是条件熵：

互信息

熵表明了单个随机变量的不确定程度，那么熵的值是确定不变的吗？我们有办法缩减这个不确定性吗？如果能缩减那缩减多少可以量化吗？

吴军老师《数学之美》：网页搜索本质正是减少不确定性的一个过程，根据用户的关键字和其他手段减少那些无关搜索，尽量接近用户的搜索意图，这种思维正可以体现信息论的“内功”本色。

一个例子来说明事件不确定性的变化：

假设现在我给你一枚硬币，告诉你这是均匀的，请你抛100次然后告诉我结果，结果你抛了100次后，记录的结果是：正面朝上90次，反面朝上10次，你就会开始怀疑“这真是一枚均匀的硬币吗？”

由第一部分熵中，我们知道，这一枚硬币的熵应该是1 bit，但是这样的试验之后，这枚硬币的熵还是1 bit吗？我们可以假设正面朝上的概率为0.9，反面朝上的概率为0.1，计算一下这个熵：

$H(X|hat{X})=-0.9log 0.9-0.1log 0.1approx0.469$

其中， $H(X| hat{X})$ 表示为知道90次正面朝上的事实后，原硬币的熵。

经过抛掷100次后，我们知道这么硬币可能是不均匀的，且新的熵为0.469 bit，也就是说我们在知道90次正面朝上，10次反面朝下的事实之后，这个硬币的熵缩小了0.531 bit，这个0.531的信息量，我们就称为互信息。

从而我们引入互信息的定义：
对于两个随机变量 $X$ 和 $Y$ ，如果其联合分布为 $p(x,y)$ ,边缘分布为 $p(x),p(y)$ ,则互信息可以定义为：
　　　　 $I(X;Y)=sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log frac{p(x,y)}{p(x)p(y)}}$
这个定义是根据相对熵来下的定义，这个定义能变成我们刚刚所说的缩减信息的形式，推导如下：

$I(X;Y)=sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log frac{p(x,y)}{p(x)p(y)}}=sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log frac{p(y)p(x|y)}{p(x)p(y)}}$ $=sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log frac{p(x|y)}{p(x)}}=sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log p(x|y)}-sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log p(x)}$ $=-sum_{xinmathcal{X}}^{}{p(x)log p(x)}-left[ -sum_{xinmathcal{X}}^{}sum_{yinmathcal{Y}}^{}{p(x,y)log p(x|y)} ight]=H(X)-H(X|Y)$

经过推导后，我们可以直观地看到 $H(X)$ 表示为原随机变量 $X$ 的信息量， $H(X|Y)$ 为知道事实 $Y$ 后 $X$ 的信息量，互信息 $I(X;Y)$ 则表示为知道事实 $Y$ 后，原来信息量减少了多少。

为了更加形象地描述互信息，文氏图来说明：

最后，如果随机变量 $X,Y$ 独立，那么互信息是多少呢？应该是0，这意味着，知道事实 $Y$ 并没有减少 $X$ 的信息量，这是符合直觉的因为独立本来就是互不影响的。

下图表示各种信息的关系，同时展示了互信息I(X,Y)的不同求法：

其中V(X,Y) (Variation of information)度量了不同随机变量/事件之间的差别，当V(X,Y)=0说明这两个变量是完全一致的，值越大则表明两个变量越独立，具体求法：

交叉熵

现在有关于样本集的两个概率分布 p(x) 和 q(x)，其中 p(x) 为真实分布， q(x)非真实分布。如果用真实分布 p(x) 来衡量识别一个样本所需要编码长度的期望（平均编码长度）为:

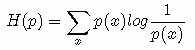
如果使用非真实分布 q(x) 来表示来自真实分布 p(x) 的平均编码长度，则是交叉熵。公式如下：

本质上可以看成用p分布的编码方式去编码q分布，所得到的编码长度期望。

举个例子。考虑一个随机变量 x，真实分布p(x)=(1/2,1/4,1/8,1/8)，非真实分布 q(x)=(1/4,1/4,1/4,1/4)，则H(p)=1.75 bits（最短平均码长），交叉熵:

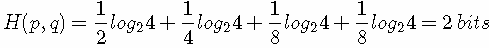
由此可以看出根据非真实分布 q(x) 得到的平均码长大于根据真实分布 p(x) 得到的平均码长。

KL散度（相对熵）公式如下：

再化简一下相对熵的公式。

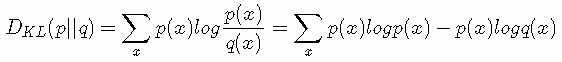
有没有发现什么？

熵的公式：

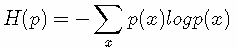
所以有：DKL(p||q)=H(p,q)−H(p)（当用非真实分布 q(x) 得到的平均码长比真实分布 p(x) 得到的平均码长多出的比特数就是相对熵）

又因为 DKL(p||q)≥0所以 H(p,q)≥H(p)（当 p(x)=q(x) 时取等号，此时交叉熵等于信息熵）并且当 H(p) 为常量时（注：在机器学习中，训练数据分布是固定的）

最小化相对熵 DKL(p||q) 等价于最小化交叉熵 H(p,q) 也等价于最大化似然估计在机器学习中，我们希望训练数据上模型学到的分布 P(model) 和真实数据的分布 P(real) 越接近越好，所以我们可以使其相对熵最小。

但是我们没有真实数据的分布，所以只能希望模型学到的分布 P(model) 和训练数据的分布 P(train) 尽量相同。

假设训练数据是从总体中独立同分布采样的，那么我们可以通过最小化训练数据的经验误差来降低模型的泛化误差。

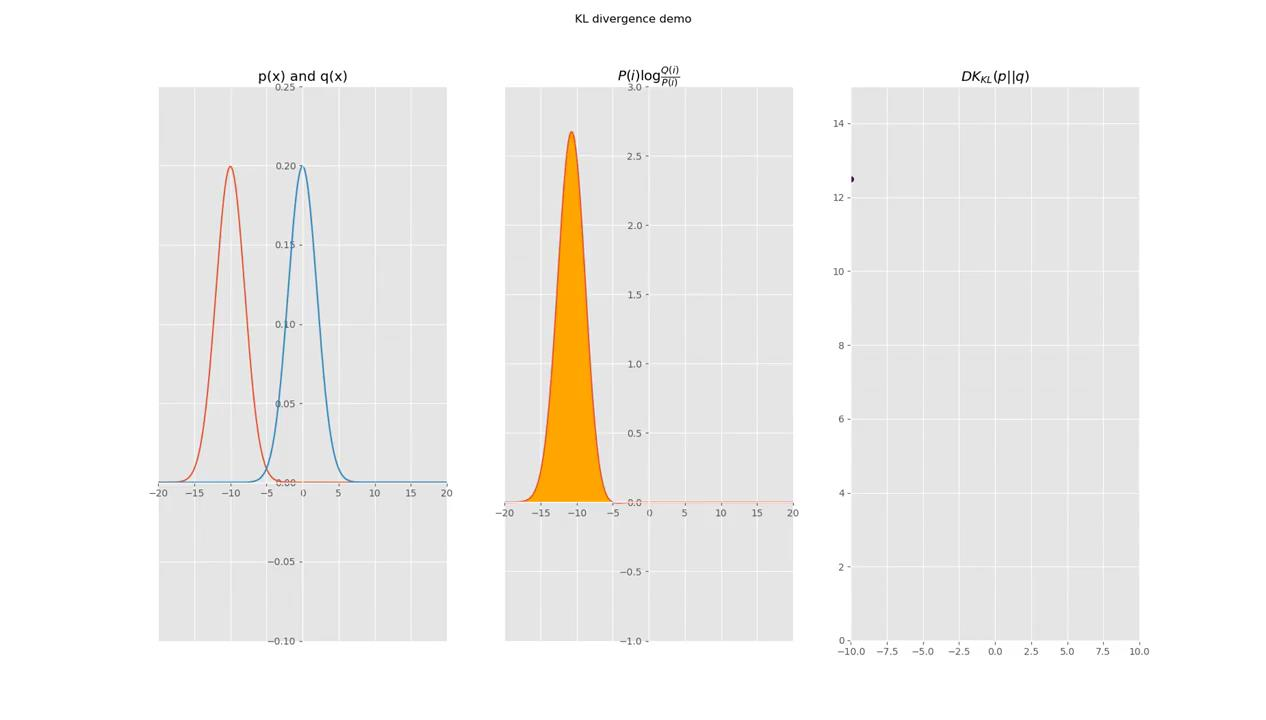
用形象化地表示三者的关系：

第一行表示p所含的信息量/平均编码长度H(p)；

第二行是cross-entropy，即用q来编码p所含的信息量/平均编码长度|或者称之为q对p的cross-entropy；

第三行是上面两者之间的差值，即q对p的KL距离，KL距离越大说明差值越大，说明两个分布的差异越大。

注意这三者都是非负的。上面说的KL和cross-entropy是两个不同分布之间的距离度量，因此用H(p)来表示熵。如果是测量同一分布中两个变量相互影响的关系，则一般用H(X)来表示熵,如联合信息熵和条件信息熵。

相对熵与KL散度

1. 概念

在概率论或信息论中，KL散度( Kullback–Leibler divergence)，又称相对熵（relative entropy)，是描述两个概率分布P和q差异的一种方法。

KL散度在信息论中物理意义，它是用来度量使用基于q分布的编码来编码来自p分布的样本平均所需的额外的Bit个数。而其在机器学习领域的物理意义则是用来度量两个函数的相似程度或者相近程度。

考虑某个未知的分布 p(x)，假定用一个近似的分布 q(x) 对它进行建模。如果我们使用 q(x) 来建立一个编码体系，用来把 x 的值传给接收者，那么由于我们使用了q(x)而不是真实分布p(x)，平均编码长度比用真实分布p(x)进行编码增加的信息量(单位是 nat )为：

$egin{aligned} KL (p || q) &= - int p(x) ln q(x) d x - (-int p(x) ln p(x) dx) \ &= - int p(x) ln [frac{q(x)}{p(x)}] dx end{aligned}$ (1)

这被称为分布p(x)和分布q(x)之间的相对熵(relative entropy)或者KL散度( Kullback-Leibler divergence )。

也就是说，当我们知道真实的概率分布之后，可以给出最有效的编码。如果我们使用了不同于真实分布的概率分布，那么我们一定会损失编码效率，并且在传输时增加的平均额外信息量至少等于两个分布之间的KL散度。

注意，这不是一个对称量，即 $KL (p || q) eq KL (q || p)$ 。

1.1. 为什么KL散度大于等于0

现在要证明的是KL散度满足 $KL (p || q) geq 0$ ,并且当且仅当 p(x) = q(x) 时等号成立。

设实直线上的函数f(x) 是一个非负函数，且：

${displaystyle int _{-infty }^{infty }f(x)\,dx=1.}$

如果 g 是任意实可测函数且函数 ${ extstyle varphi }$ 是凸的，那么有Jensen不等式如下：

${displaystyle varphi left(int _{-infty }^{infty }g(x)f(x)\,dx ight)leq int _{-infty }^{infty }varphi (g(x))f(x)\,dx.} ag{2}$

注意到，-ln x 是严格的凸函数且 $displaystyle int q(x) dx = 1$ 。

令 $varphi(x)=-ln(x)$ , $g(x)=frac {q(x)} {p(x)}$ , f(x)=p(x)

把公式(2)形式的 Jensen 不等式应用于公式(1)给出的 KL散度，直接可得

$KL (p || q) = int p(x) {-ln [frac{q(x)}{p(x)}]} d x geq - ln [int q(x) dx] = 0$ (3)

只有 q(x) = p(x) 对于所有 x 都成立时,等号才成立，

因此我们可以把 KL 散度看做两个分布 p(x) 和 q(x)之间不相似程度的度量。

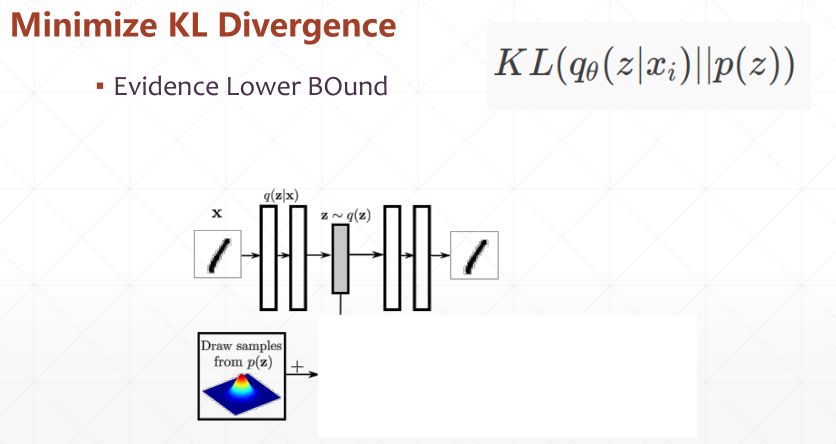
1.2. 最小化 Kullback-Leibler 散度等价于最大化似然函数

假设我们想要对未知分布p(x) 建模，可以试着使用一些参数分布 $q(x| heta)$ 来近似p(x)。 $q(x| heta)$ 由可调节的参数 $heta$ 控制(例如一个多元高斯分布)。

通过最小化 p(x) 和 $q(x| heta)$ 之间关于 $heta$ 的 KL散度可以确定 $heta$ 。

但是因为不知道 p(x)，所以不能直接这么做。

如果已经观察到了服从分布 p(x) 的有限数量的训练点集 ${x_n}$ ，其中 $n = 1,dots, N$ ，那么关于 p(x) 的期望就可以通过这些点的有限加和，使用公式 $displaystyle E(f) simeq frac{1}{N} sum_{N=1}^N f(x_n)$ 来近似，即：

$KL (p || q) simeq frac{1}{N}sum_{n=1}^N[-ln q( x_n mid heta)+ ln p( x_n)]$ (4)

公式(4)右侧的第二项与 $heta$ 无关，第一项是使用训练集估计的分布 $q(x | heta)$ 下的 $heta$ 的负对数似然函数。

因此最小化KL散度等价于最大化似然函数。

1.3. KL散度的测度论定义

如果 $mu$ 和 $u$ 是集合X上的测度，且 $mu ll u$

由Radon–Nikodym theorem， $mu$ 和 $u$ 的KL散度定义如下：

${displaystyle D_{ ext{KL}}(mu parallel u )=int _{X}log left({frac {dmu }{d u }} ight);dmu .}$

查看全文

相关阅读:
IIS 下配置无后缀的URL ReWrite
获得代理IP或客户端Ip
asp.net发送邮箱
 URLRewrite伪静态与AspNetPager分页控件的结合
 邮箱大全
 注册表单验证正则表达式
 aspx中伪静态的实现
 JMail发送邮件
 IE 6中负的margin值导致出界部分不显示问题的解决
 Culminis为每个用户组提供的免费TechNet Plus Direct订阅

原文地址：https://www.cnblogs.com/wqbin/p/12752610.html

Copyright © 2011-2022 走看看